卡通驱动项目ThreeDPoseTracker——模型驱动解析

Posted 2023-02-26 风翼冰舟

前言

之前解析过ThreeDPoseTracker这个项目中的深度学习模型，公众号有兄弟私信一些问题，我刚好对这个项目实现有兴趣，就分析一波源码，顺便把问题解答一下。

这个源码其实包括很多内容：3D姿态估计，坐标平滑，骨骼驱动，物理仿真等，非常值得分析。

参考博客：
ThreeDPoseTracker源码

理论与实现

核心代码是源码中的VNectModel.cs，主要是用预测出的3D坐标驱动卡通人体模型，包括内容有：

• 根关节位置
• 各关节旋转信息

其核心在于旋转量的确定，至于根关节位置的确定，感觉涉及到很多乱七八糟的内置参数，就不详细介绍了，但是会额外提供一个我用到天荒地老的计算方法。

如果下面的理论看不懂，推荐看看我按照源码复现的一套简化流程，一千行源码直接重写成两百多行。

预备知识——“LookRotation”

源码中有个至关重要的函数LookRotation(a,b)，它的作用是：

• 使得z轴(蓝色)始终精准指向a方向
• 使得y轴(绿色)始终偏向b方向

为什么一个是精准指向，一个是偏向，因为y和z轴是垂直的，如果a和b不垂直，那么此函数就会保证z与a同方向，y和b大致同向，看图

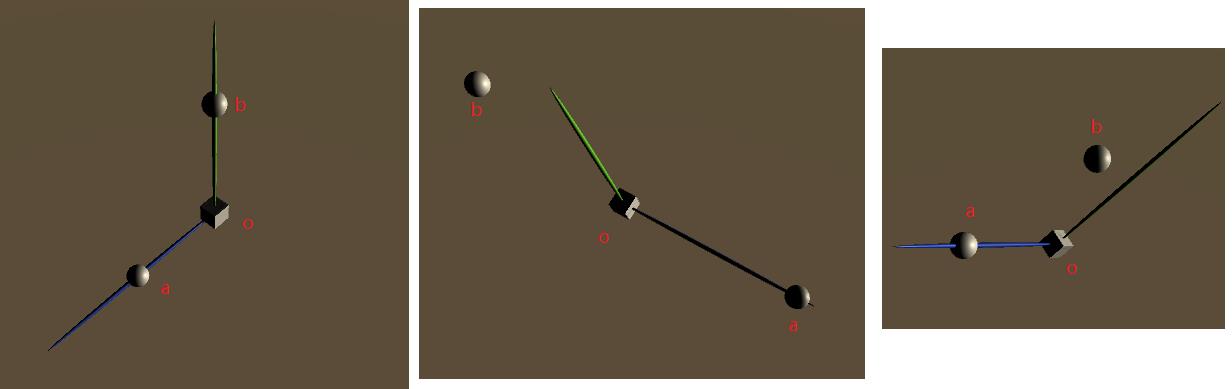
正方体为物体，绿色和蓝色分别为y和z轴，两个小球分别为y和z的目标方向。

左图为标准的指向，中间和右图为调整了目标方向后，物体的y和z的指向，可以发现，蓝色z轴始终指向目标，但是绿色y轴是偏向那个方向，因为是立体图，看着绿轴偏的很远，其实是差不多的。

总而言之，蓝轴始终是向着oa方向，绿轴向着ob与oa组成的平面中与oa垂直的方向。

驱动问题解读

如果扫过一眼代码，会发现有很多重复代码，无外乎以下几类：

初始化Init()的时候有：

AddSkeleton(xx,yy)
xx.Inverse = Quaternion.Inverse(Quaternion.LookRotation(xx.position - xxx.position, yy));
xx.InverseRotation = xx.Inverse*xx.InitRotation

驱动PoseUpdate的时候有：

xx = TriangleNormal(aa,bb,cc)
xx.rotation = Quaternion.LookRotation(yy) * xx.InverseRotation;

会发现初始化和驱动时候貌似是一种反向计算，所以才出现这么多逆(inverse)。

为什么要用LookRotation计算各个关节的旋转，而非对某根骨骼直接通过Quaternion.FromToRotation(a,b)计算出初始姿态到新的姿态下需要的旋转矩阵呢？

• 如果只用FromToRotation计算向量到向量的旋转，只能控制位置正确，无法控制方向正确，比如根关节到颈部是直着上去的，这时候人也可以侧身也可以面向前方，所以对关节必须控制至少两个方向的旋转，因此必须使用LookRotation去控制z和y轴朝向。

为什么用了LookRotation还要求这么多逆(inverse)？

• 同一个模型的不同关节具有不同的初始旋转量(即InitRotation)，而且不同人的同一个关节也可能具有不同的旋转量，甚至初始的局部坐标轴都不同，比如源码中提供的两个模型的膝盖部分局部坐标系如下

此时如果用LookRotation，不同的人就需要设置对应的规则，比如同一个姿态，左边的人蓝色z轴向后，右边人蓝色z轴向前，搞不好还有其它的情况，此时就无法用基于LookRotation的同一套代码去驱动这个人了。

如果还是不懂为什么不能用同一套代码驱动，可以举个例子：小腿向后收起的时候，左图的LookRotation必须保证蓝轴向上，右图必须保证蓝轴向下，如下图：

由于坐标轴最终的方向都不同，所以即使是同一个姿势，对于具有不同坐标系的相同关节也需要针对性LookRotation。

那么为什么源码里面可以使用LookRotation去玩驱动，很简单，因为源码将所有的关节都利用初始姿态做了LookRotation的对齐，得到了一个中间矩阵，即源码中的xx.InverseRotation，利用这个中间矩阵就能在驱动的时候对齐所有坐标系，达到通用目的。

源码分析与复现

如何实现上述问题中的坐标系对齐呢？

利用初始姿态下各关节的坐标和旋转来确定，具体是：
$$当前关节的lookrotation=初始旋转InitRotation\times 对齐矩阵$$
所以源码中的下面类似代码就是为了求解对齐矩阵：

xx.Inverse = Quaternion.Inverse(Quaternion.LookRotation(xx.position - xxx.position, yy));
xx.InverseRotation = xx.Inverse*xx.InitRotation

看不懂就可以写成

Quaternion.LookRotation(xx.position - xxx.position, yy) = xx.InitRotation * Quaternion.Inverse(xx.InverseRotation)

这就对应上述公式，其中Quaternion.Inverse(xx.InverseRotation)就对应了对齐矩阵。

因此我在复现时候，以根关节的对齐矩阵为例，把上述代码改成了

root = animator.GetBoneTransform(HumanBodyBones.Hips);
midRoot = Quaternion.Inverse(root.rotation) * Quaternion.LookRotation(forward);

其中forward是按照源码的要求，指示人体的当前方向。

如何设置LookRotation的方向？

继续分析源码，发现对于所有关节都做了

var forward = TriangleNormal(jointPoints[PositionIndex.hip.Int()].Transform.position, jointPoints[PositionIndex.lThighBend.Int()].Transform.position, jointPoints[PositionIndex.rThighBend.Int()].Transform.position);
jointPoint.Inverse = GetInverse(jointPoint, jointPoint.Child, forward);
                jointPoint.InverseRotation = jointPoint.Inverse * jointPoint.InitRotation;

第一行，基于根关节和左右胯关节坐标计算出人体朝向，然后以此作为所有关节的LookRotation的y方向，以及每个关节与其子关节的方向作为z方向，计算出中间矩阵。

注意，在接下来，分别对头部和手掌单独又计算了一遍，因为他俩比较特殊

对于头部，直接求解出头到鼻子的向量作为LookRotation的z方向，未设置y方向。

var gaze = jointPoints[PositionIndex.Nose.Int()].Transform.position - jointPoints[PositionIndex.head.Int()].Transform.position; // head的方向是head->Nose
head.Inverse = Quaternion.Inverse(Quaternion.LookRotation(gaze));

然后计算头部的中间矩阵

head.Inverse = Quaternion.Inverse(Quaternion.LookRotation(gaze));
        head.InverseRotation = head.Inverse * head.InitRotation;

对于手腕，直接利用手腕、大拇指、中指的坐标，计算出手掌方向作为LookRotation的y方向，

var lf = TriangleNormal(lHand.Pos3D, jointPoints[PositionIndex.lMid1.Int()].Pos3D, jointPoints[PositionIndex.lThumb2.Int()].Pos3D); // 手掌方向
var rf = TriangleNormal(rHand.Pos3D, jointPoints[PositionIndex.rThumb2.Int()].Pos3D, jointPoints[PositionIndex.rMid1.Int()].Pos3D);

而左手腕以大拇指到中指的方向为z方向，而右手腕以中指到大拇指方向为z方向：

lHand.Inverse = Quaternion.Inverse(Quaternion.LookRotation(jointPoints[PositionIndex.lThumb2.Int()].Transform.position - jointPoints[PositionIndex.lMid1.Int()].Transform.position, lf));
rHand.Inverse = Quaternion.Inverse(Quaternion.LookRotation(jointPoints[PositionIndex.rThumb2.Int()].Transform.position - jointPoints[PositionIndex.rMid1.Int()].Transform.position, rf));

再分别求解出中间矩阵：

lHand.InverseRotation = lHand.Inverse * lHand.InitRotation;
rHand.InverseRotation = rHand.Inverse * rHand.InitRotation;

其实完全没必要区分这么明显，只需要求解和使用的时候对应好就行了，比如我实现的时候就统一大拇指到中指：

midLhand = Quaternion.Inverse(lhand.rotation) * Quaternion.LookRotation(
            lthumb2.position - lmid1.position,
            TriangleNormal(lhand.position, lthumb2.position, lmid1.position)
            );
midRhand = Quaternion.Inverse(rhand.rotation) * Quaternion.LookRotation(
            rthumb2.position - rmid1.position,
            TriangleNormal(rhand.position, rthumb2.position, rmid1.position)
            );

也就是说，对于某些特定关节，需要单独设置用于计算中间变换矩阵的LookRotation信息。推荐看我实现的源码，分为躯干、头、手掌三个部分，我实现的源码就不贴了，文末找。

注意这里计算初始姿态中各关节的LookRotation方法与运行时从深度学习预测的3D关节坐标中计算的LookRotation方案要一模一样。

如何驱动？

通过
$$当前关节的lookrotation=初始旋转InitRotation\times 对齐矩阵$$
得到了每个关节的对齐矩阵，那么这个公式很容易得到每个关节的当前旋转信息：
$$当前旋转Rotation=当前关节的lookrotation\times Quaternion.Inverse(对齐矩阵)$$
然后分析源码，在PoseUpdate()函数中，前面的不用看，是计算根关节坐标的，我们先关注关节旋转。

注意因为用对齐矩阵是从初始姿态获取的，所以如何依据初始姿态计算的lookrotation就要按照同样的方法从深度学习模型预测的3D关节坐标中计算对应的lookrotation参数。

比如人体方向依旧是根、左右胯部的坐标计算：

var forward = TriangleNormal(jointPoints[PositionIndex.hip.Int()].Pos3D, jointPoints[PositionIndex.lThighBend.Int()].Pos3D, jointPoints[PositionIndex.rThighBend.Int()].Pos3D);

而根关节当前的旋转就是根据上述公式计算得到：

jointPoints[PositionIndex.hip.Int()].Transform.rotation = Quaternion.LookRotation(forward) * jointPoints[PositionIndex.hip.Int()].InverseRotation;

其它关节我不贴源码了，直接描述：

躯干关节：以身体方向为LookRotation的y方向，以当前关节到其子关节的方向为z方向。

手腕：以手腕、大拇指、中指形成的平面的法线方向为y方向，以拇指到中指的方向为z方向。

比如我随便贴一下我复现的左臂(肩、肘、腕)实时驱动：

// 左臂
lshoulder.rotation = Quaternion.LookRotation(pred3D[5] - pred3D[6], forward) * Quaternion.Inverse(midLshoulder);
lelbow.rotation = Quaternion.LookRotation(pred3D[6] - pred3D[7], forward) * Quaternion.Inverse(midLelbow);
lhand.rotation = Quaternion.LookRotation(pred3D[8] - pred3D[9],
    TriangleNormal(pred3D[7], pred3D[8], pred3D[9]))*Quaternion.Inverse(midLhand);

其中pred3D就是深度学习模型预测的3D关节坐标。

人体位置

上述讲解了旋转的计算方法，关于整个人体的位置，源码中自有一套方案，但是里面预设了很多固定参数，不是特别想分析，所以用了万年不变的方法，计算unity人物模型腿的长度和深度学习预测的腿部长度，然后计算比例系数，乘到深度学习预测的根关节位置即可。

float tallShin = (Vector3.Distance(pred3D[16], pred3D[17]) + Vector3.Distance(pred3D[20], pred3D[21]))/2.0f;
float tallThigh = (Vector3.Distance(pred3D[15], pred3D[16]) + Vector3.Distance(pred3D[19], pred3D[20]))/2.0f;
float tallUnity = (Vector3.Distance(lhip.position, lknee.position) + Vector3.Distance(lknee.position, lfoot.position)) / 2.0f +
    (Vector3.Distance(rhip.position, rknee.position) + Vector3.Distance(rknee.position, rfoot.position));
root.position = pred3D[24] * (tallUnity/(tallThigh+tallShin));

是不是超级简单，虽然效果有点偏差，但是后续还是会分析一下源码中更新人体位置的方案。

复现流程

在VNectModel.cs中的PoseUpdate函数加入以下代码：

FileStream fs = new FileStream(@"D:\\code\\Unity\\ThreeDExperiment\\Assets\\Resources\\record.txt", FileMode.Append);
StreamWriter sw = new StreamWriter(fs);
//写入
foreach(JointPoint jointPoint in jointPoints)

    sw.Write(jointPoint.Pos3D.x.ToString() + " " + jointPoint.Pos3D.y.ToString() + " " + jointPoint.Pos3D.z.ToString() + " ");
        
sw.WriteLine();
sw.Flush();
sw.Close();
fs.Close();

将关键点写入到txt中做复现时候用的3D关键点数据

然后按照理论进行复现后效果如下：

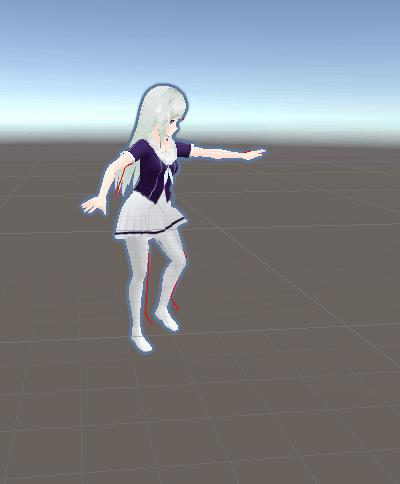
红色为预测的3D坐标，人物模型会做出与红色骨架一样的姿势。

结论

这个感觉还是没有考虑人体运动的动力学特性，如果跑过源码，很容易发现个别姿势会出现奇怪的关节扭曲现象，这就是不考虑动力学的后果，给我自己之前的代码打一波广告，那个绝对比这个好，哈哈。

完整的unity实现放在微信公众号的简介中描述的github中，有兴趣可以去找找。或者在公众号回复“ThreeDPose"，同时文章也同步到微信公众号中，有疑问或者兴趣欢迎公众号私信。