C# 各种内部排序方法的实现(直接插入排序希尔排序冒泡排序快速排序直接选择排序堆排序归并排序基数排序)
Posted 不如詩啊
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了C# 各种内部排序方法的实现(直接插入排序希尔排序冒泡排序快速排序直接选择排序堆排序归并排序基数排序)相关的知识,希望对你有一定的参考价值。
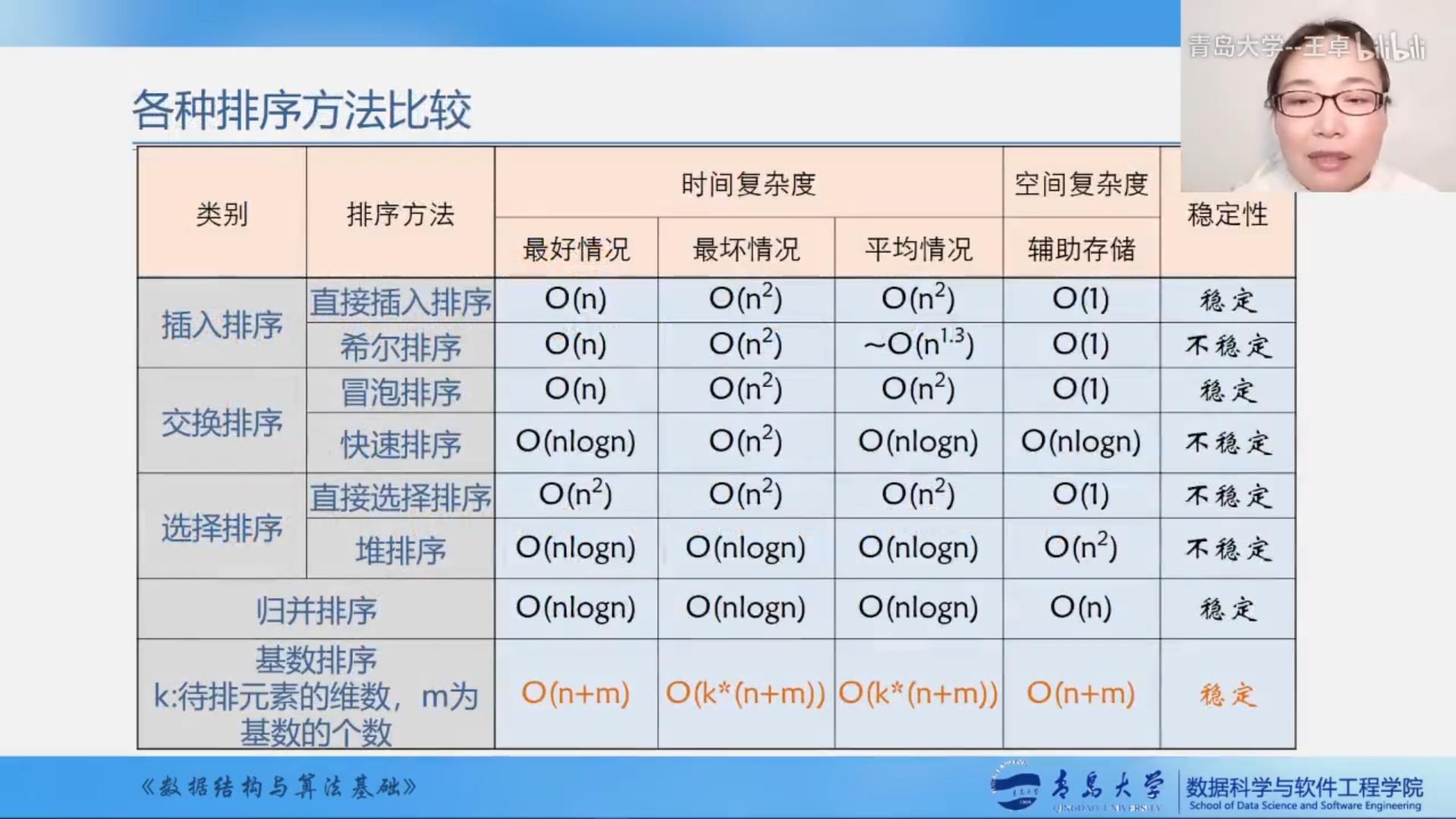
C# 各种内部排序方法的实现(直接插入排序、希尔排序、冒泡排序、快速排序、直接选择排序、堆排序、归并排序、基数排序)
以下代码为我在学习数据结构时自己敲出来的,除了主函数中的代码外没有做其他的测试,如有问题希望大家指出。
数据结构学习视频为青岛大学王卓老师制作,网址:https://www.bilibili.com/video/BV1nJ411V7bd?
- SqList类的实现(各排序方法均为类内部方法)
/// <summary>
/// 顺序存储结构(0号位置为缓冲区)
/// </summary>
class SqList
public class RedType
public int key; //关键字
public string otherInfo; //其他数据项
private int capacity;
private RedType[] r;
private int length;
public int Length get => length; private set => length = value;
public int Capacity get => capacity; private set => capacity = value;
public RedType this[int index] get => r[index]; set => r[index] = value;
public SqList(int capacity)
this.capacity = capacity;
r = new RedType[capacity + 1]; //r[0]一般作哨兵或缓冲区
for (int i = 0; i < capacity + 1; i++)
r[i] = new RedType();
length = 0;
public SqList() : this(20)
/// <summary>
/// 添加元素
/// </summary>
/// <param name="values"></param>
public void Add(params int[] values)
if (values.Length > this.capacity - this.length)
throw new ArgumentException("顺序表容量不足");
int startIndex = this.length + 1;
for (int i = 0; i < values.Length; i++)
r[startIndex + i].key = values[i];
length++;
/// <summary>
/// 重写ToString方法
/// </summary>
/// <returns></returns>
public override string ToString()
StringBuilder sb = new StringBuilder();
for (int i = 1; i <= this.length; i++)
sb.Append(r[i].key + " ");
return sb.ToString();
#region 插入排序(直接插入排序, 折半插入排序, 希尔排序)
/// <summary>
/// 直接插入排序(使用"哨兵")
/// 最坏情况下Tw(n) = O(n²)
/// 平均情况下Te(n) = O(n²)
/// 稳定
/// </summary>
public void SInsertSort()
for (int i = 2; i <= this.length; i++)
if (r[i].key > r[i - 1].key) //i前面的元素已经有序, 所以若i位置的元素大于前一个元素, 则不用移动它
continue;
r[0] = r[i]; //将i元素放到"哨兵"位置
int j;
for (j = i - 1; r[0].key < r[j].key; j--) //记录后移, 找到插入位置
r[j + 1] = r[j];
r[j + 1] = r[0]; //插入到正确位置
/// <summary>
/// 折半插入排序(带"哨兵")
/// 平均性能优于直接插入排序
/// 时间复杂度O(n²)
/// 稳定
/// </summary>
public void BInsertSort()
for (int i = 2; i <= this.length; i++)
r[0] = r[i];
int low = 1, high = i - 1, mid;
while (low <= high)
mid = (low + high) / 2;
if (r[0].key < r[mid].key)
high = mid - 1;
else
low = mid + 1;
//循环结束, high+1为插入位置
for (int j = i - 1; j > high; j--)
r[j + 1] = r[j];
r[high + 1] = r[0];
/// <summary>
/// 希尔排序
/// 算法效率与增量序列dlta的取值有关
/// Hibbard增量序列 dlta[k] = 2^(k-1) 相邻元素互质
/// 最坏情况Tw = O(n^(3/2))
/// 猜想Ta = O(n^(5/4))
/// Sedgewick增量序列1, 5, 19, 41, 109, ... dlta[k] = 9*4^i-9*2^i+1 或 4^i-3*2^i+1
/// 猜想: Ta = O(n^(7/6)) Tw = O(n^(4/3))
/// 不稳定
/// </summary>
/// <param name="dlta">增量序列(必须是递减的且互质的, 最后一个必须是1)</param>
public void ShellSort(int[] dlta)
for (int i = 0; i < dlta.Length; i++)
ShellInsert(dlta[i]);
/// <summary>
/// 希尔排序中某一趟的操作
/// </summary>
/// <param name="dk">步长因子</param>
private void ShellInsert(int dk)
for (int i = dk + 1; i <= this.length; i++) //i从第dk+1个元素开始向后到表尾(步长为1)
if (r[i].key > r[i - dk].key) //若比前一个大,则不需要进行移动
continue;
r[0] = r[i]; //将元素i放到哨兵位置
int j;
for (j = i - dk; j > 0 && r[0].key < r[j].key; j -= dk) //j从i-dk个元素开始向前到表头(步长为dk)
r[j + dk] = r[j];
r[j + dk] = r[0];
#endregion
#region 交换排序(冒泡排序, 快速排序)
/// <summary>
/// 冒泡排序
/// Tb = O(n); Tw = O(n²); Ta = O(n²)
/// 稳定
/// </summary>
public void BubbleSort()
bool isSorded = false; //用来记录每一趟是否没有发生逆序, 若没有发生逆序, 则说明该列表已经有序
for (int i = 1; i < this.length && !isSorded; i++) //需要进行this.length-1趟
isSorded = true;
for (int j = 1; j <= this.length - i; j++)
if (r[j].key > r[j + 1].key) //若前者大于后者(发生了逆序)于则交换
r[0] = r[j];
r[j] = r[j + 1];
r[j + 1] = r[0];
isSorded = false; //发生了逆序, 将标记记为false
/// <summary>
/// 快速排序
/// 平均之间复杂度为O(nlog2n);
/// 平均空间复杂度为O(logn), 最坏情况下为O(n)
/// 不稳定
/// </summary>
/// <param name="firstIndex"></param>
/// <param name="lastIndex"></param>
public void QuickSort(int firstIndex, int lastIndex)
if (lastIndex <= firstIndex)
return;
int low = firstIndex; //前指针
int high = lastIndex; //后指针
r[0] = r[low]; //挖出第一个元素(中心元素), 放到哨兵位置
//此时坑在front
while (low < high)
while (low < high && r[high].key >= r[0].key)
high--;
r[low] = r[high]; //挖出该元素, 放到坑里
//此时坑在behind
while (low < high && r[low].key <= r[0].key)
low++;
r[high] = r[low]; //挖出该元素, 放到坑里
//此时坑在front
//前后指针已经重合
r[low] = r[0]; //将中心元素填入坑内
QuickSort(firstIndex, low - 1);
QuickSort(low + 1, lastIndex);
/// <summary>
/// 快速排序
/// 平均之间复杂度为O(nlog2n);
/// 平均空间复杂度为O(logn), 最坏情况下为O(n)
/// 不稳定
/// </summary>
public void QuickSort()
QuickSort(1, this.length);
#endregion
#region 选择排序(简单选择排序)
/// <summary>
/// 简单选择排序
/// 移动次数最低:0, 最高: 3(n-1);
/// 比较次数: (n/2)*(n-1)
/// 不稳定
/// </summary>
public void SSelectionSort()
for (int i = this.Length; i > 1; i--)
int maxIndex = i;
for (int j = i - 1; j >= 1; j--)
if (r[j].key > r[maxIndex].key)
maxIndex = j;
r[0] = r[i];
r[i] = r[maxIndex];
r[maxIndex] = r[0];
/// <summary>
/// 堆排序
/// 无论什么情况, 时间复杂度均为O(nlog₂n);
/// 不稳定
/// </summary>
public void HeapSort()
//构建大根堆
for (int i = this.Length / 2; i > 0; i--) //从最后一个非叶子节点(n/2)开始, 依次向前调整
HeapAdjust(1, this.length, i); //每一个非叶子节点都筛选一遍
for (int i = this.length; i >= 2; i--) //进行n=1趟排序
//将根与最后一个元素交换(将最大值放到最后)
r[0] = r[1];
r[1] = r[i];
r[i] = r[0];
HeapAdjust(1, i - 1, 1);
//此时最小元素在根部
//最后一个元素放到根部
/// <summary>
/// 堆排序的筛选操作(从某一个非叶子节点开始, 与其左右子树的根节点进行比较, 并与其中较大者进行交换, 重复上述操作直到叶子节点)
/// </summary>
/// <param name="low">堆的起始索引</param>
/// <param name="high">堆的结束索引</param>
/// <param name="rootIndex">起始非叶子节点的索引</param>
private void HeapAdjust(int low, int high, int rootIndex)
int n = high - low + 1; //元素个数
r[0] = r[rootIndex]; //将需要筛选的元素放到哨兵位置
for (int i = 2 * rootIndex; i <= n; i *= 2) //沿key较小的孩子节点向下筛选
if (i < n && r[i].key < r[i + 1].key) //i为左右孩子节点中较大者的的索引
i++;
if (r[i].key <= r[0].key) //若左右孩子较小的都没有哨兵大, 则跳出循环
break;
r[rootIndex] = r[i]; //将较大的孩子节点放到它的父节点
rootIndex = i; //r[0]应该插入到rootIndex位置
r[rootIndex] = r[0]; //找到插入位置后, 将哨兵插入到该位置
#endregion
#region 归并排序
/// <summary>
/// 归并排序
/// 时间效率O(nlog₂n);
/// 空间效率O(n)
/// 稳定
/// </summary>
public void MergeSort()
RedType[] tr = new RedType[r.Length]; //临时数组
for (int i = 0; i < tr.Length; i++) //初始化临时数组
tr[i] = new RedType();
int n = 1; //归并范围(参与归并的前后数组元素之和)
do
n *= 2; //更新n
int k = 1; //临时数组指针
for (int i = 1; i <= this.length; i += n) //每两组进行归并
int p1 = i; //前数组指针
int m = i + n / 2 - 1; //前数组后边界
int high = i + n - 1; //后数组后边界
int p2 = m + 1; //后数组指针
if (m < this.length) //若m没有超过数组界限
high = high < this.length ? high : this.length; //判断high是否超过数组界限
else //若m超过数组界限
m = this.length;
p2 = high + 1; //给p2一个垃圾值, 让其不参与运算
//将前后数组存入临时数组中
while (p1 <= m || p2 <= high) //只要两个指针没有都走完
if (p1 <= m && p2 <= high) //若两个都没走完
//将p1和p2指向的元素中较小的存入临时数组
if (r[p1].key <= r[p2].key)
tr[k] = r[p1];
p1++;
else
tr[k] = r[p2];
p2++;
else if (p1 <= m) //若p2走完, 且p1没走完
tr[k] = r[p1];
p1++;
else if (p2 <= high) //若p1走完, 且p2没走完
tr[k] = r[p2];
p2++;
k++;
//一次归并结束
//更新数组
for (int i = 0; i < r.Length; i++)
r[i] = tr[i];
//Console.WriteLine(this);
while (n <