动态规划 学习笔记
Posted 若曦`
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了动态规划 学习笔记相关的知识,希望对你有一定的参考价值。
1.动态规划步骤
(1)确定dp数组以及下标的含义
(2)确定递推公式
(3)dp数组初始化
(4)确定遍历顺序
(5)举例推导dp数组
2. 一维dp数组做题记录
做题由简到难记录
入门/简单题
爬楼梯

(1)确定dp[i]含义
- i表示阶梯层数
- dp[i]表示到达阶梯i有多少种跳法
(2) 确定递推公式
- dp[i] = dp[i-1]+dp[i-2]
说明:因为对于阶梯i,其跳法=上一级跳一阶+上上一级跳两阶
所以跳上阶梯i的跳法= 阶梯[i-1]+阶梯[i-2]
(3)初始化dp[i]
dp[0] = 0; //阶梯为0
dp[1] = 1; //阶梯为1 1种
dp[2] = 2; //阶梯为2 2种
(4)确定遍历顺序
此题遍历顺序比较简单,将1~N每级阶梯遍历一次即可
(5)举例推导
纸上画一下dp表对应比照一下
(6)写出代码
class Solution
public int climbStairs(int n)
if(n<=2)
return n;
int[] dp = new int[n];
dp[0] = 0;
dp[1] = 1;
dp[2] = 2;
for(int i=3;i<n;i++)
dp[i] = dp[i-1]+dp[i-2];
//最后一个阶梯的结果=[n-1]+[n-2]
return dp[n-1]+dp[n-2];
使用最小花费爬楼梯

(1)确定dp[i]含义
- i表示第i级阶梯
- dp[i]表示到达第i级阶梯花费的最小体力值
(2)确定递推公式
dp[i] = Math.min(dp[i-1],dp[i-2])+cost[i]
说明:当前阶梯花费最少体力值= 能跳上该阶梯时的最少体力值+当前阶梯花费的体力值
(3)dp初始化
dp[0] = cost[0];
dp[1] = cost[1];
(4)确定遍历顺序
同样将所有阶梯遍历一遍
(5)举例推导dp数组
画图举例
(6)写代码
class Solution
public int minCostClimbingStairs(int[] cost)
if(cost.length<=1)
return cost[cost.length];
int[] dp = new int[cost.length];
dp[0] = cost[0];
dp[1] = cost[1];
for(int i=2;i<cost.length;i++)
dp[i] = Math.min(dp[i-1],dp[i-2])+cost[i];
//最后可以从最后一个阶梯跳,或者倒数第二个阶梯跳上去
return Math.min(dp[cost.length-1],dp[cost.length-2]);
最大子序和

(1)确定dp[i]含义
- i表示第nums[]的第i个下标
- dp[i]表示nums[i]被选择后,得到的子序和
(2)确定递推方向
dp[i] = dp[i-1]>0?dp[i-1]+nums[i]:nums[i];
不解释了,比较简单
(3)初始化dp
dp[0] = nums[0];
(4)确定遍历顺序
对nums[]数组正序遍历一次即可
(5)举例推导dp数组
画图得证
(6)写代码
class Solution
int res=0;
public int maxSubArray(int[] nums)
int len = nums.length;
int[] dp = new int[len];
int max = nums[0];
dp[0] = nums[0];
for(int i=1;i<len;i++)
dp[i] = dp[i-1]>0?dp[i-1]+nums[i]:nums[i];
if(dp[i]>max)
max = dp[i];
return max;
中等题
打家劫舍

(1)确定dp[i]的含义
- i表示房间号
- dp[i]表示偷到对应房间号为止,最大的金额
(2)确定推导公式
- dp[i] = Math.max(dp[i-3]+dp[i-2])+nums[i]
说明:因为要间隔,画图就明白,只有两种选择 i-2或i-3
(3)dp初始化
dp[0] = nums[0];
dp[1] = nums[1];
dp[2] = nums[0]+nums[2];
(4)确定遍历顺序
对每个房间遍历一次
(5)举例推导dp数组
画图得证
(6)写出代码
class Solution
public int rob(int[] nums)
if(nums.length==1)
return nums[0];
if(nums.length==2)
return Math.max(nums[0],nums[1]);
int[] dp = new int[nums.length];
dp[0] = nums[0];
dp[1] = nums[1];
dp[2] = nums[0]+nums[2];
for(int i=3;i<nums.length;i++)
dp[i] = Math.max(dp[i-3],dp[i-2])+nums[i];
return Math.max(dp[nums.length-2],dp[nums.length-1]);
打家劫舍 II
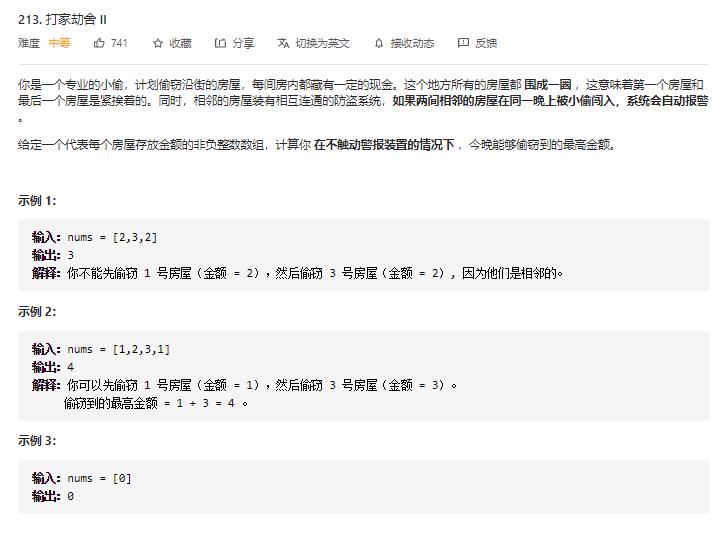
做法和打家劫舍1差不多。区别只是区分一下房间1选择和不选择的两种情况,分别计算值,取最大值作为结果
class Solution
public int rob(int[] nums)
int len = nums.length;
if(len<=2)
if(len==1)
return nums[0];
return Math.max(nums[0],nums[1]);
else if(len==3)
if(nums[0]>nums[1])
return Math.max(nums[0],nums[2]);
else
return Math.max(nums[1],nums[2]);
int[] dp = new int[nums.length];
//第一种可能 房间1必偷 最后一个房间不偷
dp[0] = nums[0];
dp[1] = 0;
dp[2] = nums[0]+nums[2];
dp[3] = nums[0]+nums[3];
for(int i=4;i<nums.length;i++)
dp[i] = Math.max(dp[i-3],dp[i-2])+nums[i];
//拿倒数第三个房间和倒数第二个房间比较 取最大
int max1 = Math.max(dp[nums.length-3],dp[nums.length-2]);
//第二种可能 房间1不偷 最后一个房间必偷
dp[0] = 0;
dp[1] = nums[1];
dp[2] = nums[2];
dp[3] = nums[1]+nums[3];
for(int i=4;i<nums.length;i++)
dp[i] = Math.max(dp[i-3],dp[i-2])+nums[i];
//拿倒数第二个房间和倒数第一个房间比较 取最大
int max2 = Math.max(dp[nums.length-2],dp[nums.length-1]);
//返回房间1偷与不偷的最大选择值
return Math.max(max1,max2);
by ruoxi 8.4
删除并获得点数

提示:如果深刻理解了此题的做法,那么此题和打家劫舍的做法类似
首先,我们先明确一个概念,就是每个位置上的数字是可以在两种前结果之上进行选择的:
如果你不删除当前位置的数字,那么你得到就是前一个数字的位置的最优结果。
如果你觉得当前的位置数字i需要被删,那么你就会得到i - 2位置的那个最优结果加上当前位置的数字乘以个数。
以上两个结果,你每次取最大的,记录下来,然后答案就是最后那个数字了。
上述的每个位置上的数字,指的是像存储1,2,3,4,5这种自然数个数的数组
那么可以创建一个count[]数组,用于存储每个自然数在nums[]中出现的次数
count的长度=nums[]数组中的最大值(max)
比如nums[] = 1,1,2,3,3,3,那么count[]=0,2,1,3
说明:0在nums中出现了0次 1出现了2次 2出现1次 3出现3次
(1)明确dp[i]的含义
- i表示选择自然数i
- dp[i]表示选择i后能得到的最大点数
这里的dp[i]长度也就等于count的长度,因为dp[i]是选择自然数i,count存储的是自然数i出现的次数
(2)找出递推公式
- dp[i] = Math.max(dp[i-1],dp[i-2]+i*count[i])
(3)初始化dp
dp[0] = 0; //因为选择0,无论多少个0都是0
dp[1] = nums中1出现的次数*1
(4)确定遍历顺序
对count[]数组遍历一遍即可
(5)举例推导dp数组
画图举例得证
(6)写代码
class Solution
public int deleteAndEarn(int[] nums)
int len = nums.length;
if(len==0)
return 0;
//获取nums数组的最大值
int max = 0;
for(int i=0;i<len;i++)
if(nums[i]>max)
max = nums[i];
//创建count数组,存储每个数字值在nums[]中存在的个数
int[] count = new int[max+1];
//创建dp数组
int[] dp = new int[max+1];
//num数字值也就对应count数组的下标
//顺带初始化dp
for(int num : nums)
count[num] ++;
if(num==1)
dp[1] +=1;
dp[0] = 0;
if(max==1)
return dp[1];
//递推方向 :dp[i] = Math.max(dp[i-1],dp[i-2]+count[i]*i)
for(int i=2;i<max+1;i++)
dp[i] = Math.max(dp[i-1],dp[i-2]+count[i]*i);
return Math.max(dp[max],dp[max-1]);
持续更新中…
3. 二维dp数组做题记录
中等题
不同路径

解释:对于每个方格来说,都必须从该方格的左边或者上面的方格走下来,也就是根据上两个位置的结果而定,所以很明显发觉可以用动态规划来解题
(1)确定dp数组以及下标的含义
- i代表行数,j代表列数,dp[i][j]代表到达[i][j]处有多少条路径方法
(2)确定递推公式
- dp[i][j] = dp[i-1][j]+dp[i][j-1];
(3)dp数组初始化
- 对于第一列和第一行,都只能向右或向下走,只有一种方式
(4)确定遍历顺序
- 对二维数组每个下标都遍历一遍
(5)举例推导dp数组
- 稍微测试一下就行
(6)写代码
class Solution
public int uniquePaths(int m, int n)
int[][] dp = new int[m][n];
for(int i=0;i<m;i++)
dp[i][0]=1;
for(int i=0;i<n;i++)
dp[0][i]=1;
for(int i=1;i<m;i++)
for(int j=1;j<n;j++)
dp[i][j] = dp[i-1][j]+dp[i][j-1];
return dp[m-1][n-1];
以上是关于动态规划 学习笔记的主要内容,如果未能解决你的问题,请参考以下文章
Leetcode算法初学——动态规划算法“使用最小花费爬楼梯”