Attention机制学习记录

Posted 2022-11-23 彭祥.

Attention机制的本质思想

首先是对注意力机制的计算过程进行总结：
带有 Attention 机制的 Encoder-Decoder 模型则是要从序列中学习到每一个元素的重要程度，然后按重要程度将元素合并。因此，注意力机制可以看作是 Encoder 和 Decoder 之间的接口，它向 Decoder 提供来自每个 Encoder 隐藏状态的信息。通过该设置，模型能够选择性地关注输入序列的有用部分，从而学习它们之间的“对齐”。这就表明，在 Encoder 将输入的序列元素进行编码时，得到的不在是一个固定的语义编码 C ，而是存在多个语义编码，且不同的语义编码由不同的序列元素以不同的权重参数组合而成。一个简单地体现 Attention 机制运行的示意图如下：

定义：对齐
对齐是指将原文的片段与其对应的译文片段进行匹配。

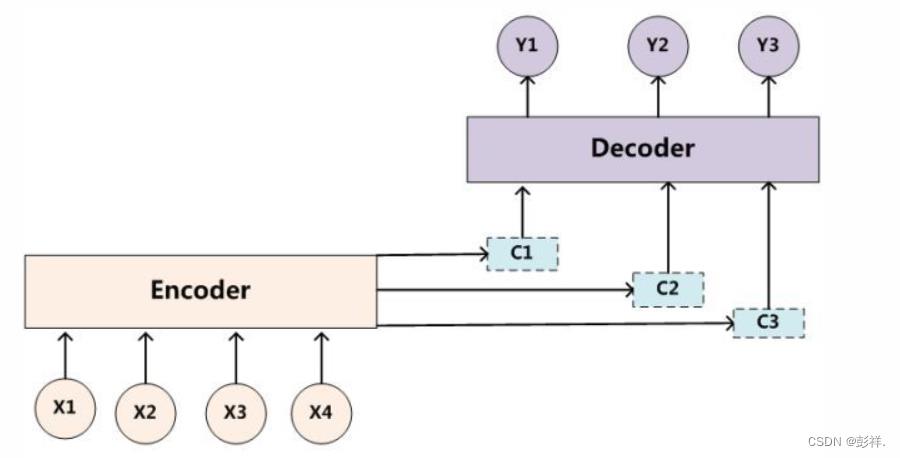
在 Attention 机制下，语义编码 C 就不在是输入序列 X 的直接编码了，而是各个元素按其重要程度加权求和得到的，即：

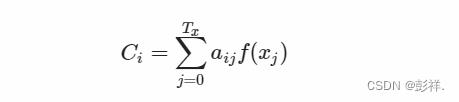
上式中，参数 i 表示时刻， j 表示序列中的第 j 个元素， T_x 表示序列的长度， f(⋅) 表示对元素 x_j 的编码(这个值有时为h_j)。a_ij 可以看作是一个概率，反映了元素 h_j 对 C_i 的重要性，可以使用 softmax 来表示：

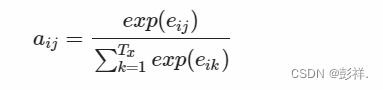
这里 e_ij 正是反映了待编码的元素和其它元素之间的匹配度，当匹配度越高时，说明该元素对其的影响越大，则 a_ij 的值也就越大。

因此，得出 aij 的过程如下图：

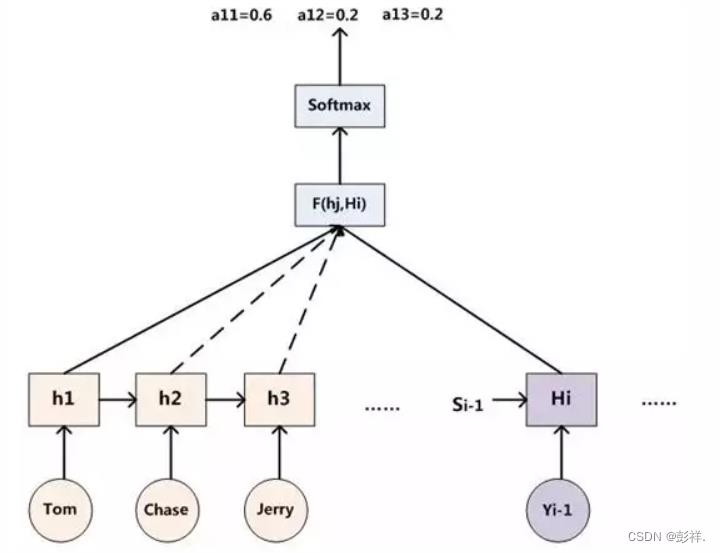
其中，hi 表示 Encoder 的转换函数，F(hj,Hi) 表示预测与目标的匹配打分函数。将以上过程串联起来，则注意力模型的结构如下图所示：

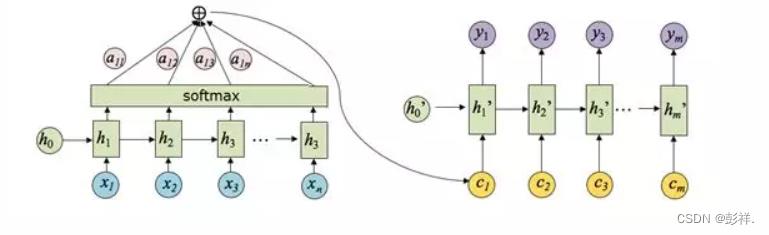
如果把Attention机制从Encoder-Decoder框架中剥离，并进一步做抽象，可以更容易看懂Attention机制的本质思想。这种其实应该是self-attention 的思想，其中引入了三个非常重要的元素： Query 、Key 和 Value。当然由于self-attention与attention的区别在于签证只在一个source中，而后者缺需要source和target,这里的query可以认为是解码器的隐藏层单元输出。

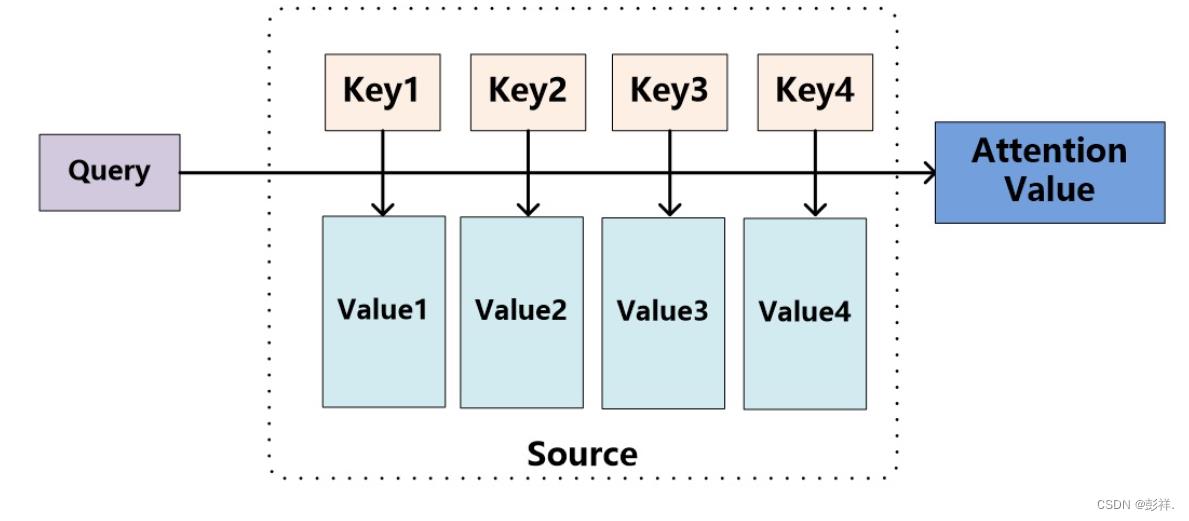
将Source中的构成元素想象成是由一系列的<Key,Value>数据对构成，此时给定Target中的某个元素Query（这里可以认为是解码器的隐藏状态），通过计算Query和各个Key的相似性或者相关性，得到每个Key对应Value的权重系数，然后对Value进行加权求和（在自然语言任务中，往往 Key 和 Value 是相同的，比如对应hi），即得到了最终的Attention数值（即为语义编码C)。所以本质上Attention机制是对Source中元素的Value值进行加权求和，而Query和Key用来计算对应Value的权重系数。即可以将其本质思想改写为如下公式：

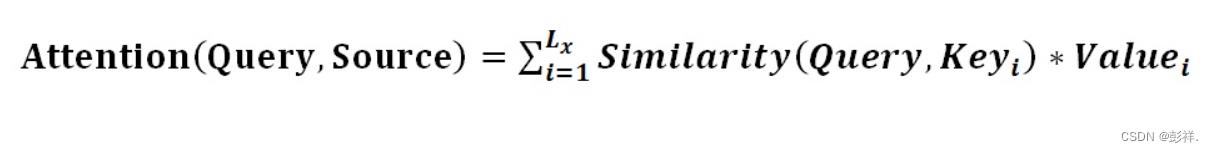
可以将Attention机制看作一种软寻址（Soft Addressing）:Source可以看作存储器内存储的内容，元素由地址Key和值Value组成，当前有个Key=Query的查询，目的是取出存储器中对应的Value值，即Attention数值。通过Query和存储器内元素Key的地址进行相似性比较来寻址，之所以说是软寻址，指的不像一般寻址只从存储内容里面找出一条内容，而是可能从每个Key地址都会取出内容，取出内容的重要性根据Query和Key的相似性来决定，之后对Value进行加权求和，这样就可以取出最终的Value值，也即Attention值。所以不少研究人员将Attention机制看作软寻址的一种特例，这也是非常有道理的。

Attention机制的具体计算过程，如果对目前大多数方法进行抽象的话，可以将其归纳为两个过程：第一个过程是根据Query和Key计算权重系数，第二个过程根据权重系数对Value进行加权求和。而第一个过程又可以细分为两个阶段：第一个阶段根据Query和Key计算两者的相似性或者相关性；第二个阶段对第一阶段的原始分值进行归一化处理；这样，可以将Attention的计算过程抽象为如图展示的三个阶段。

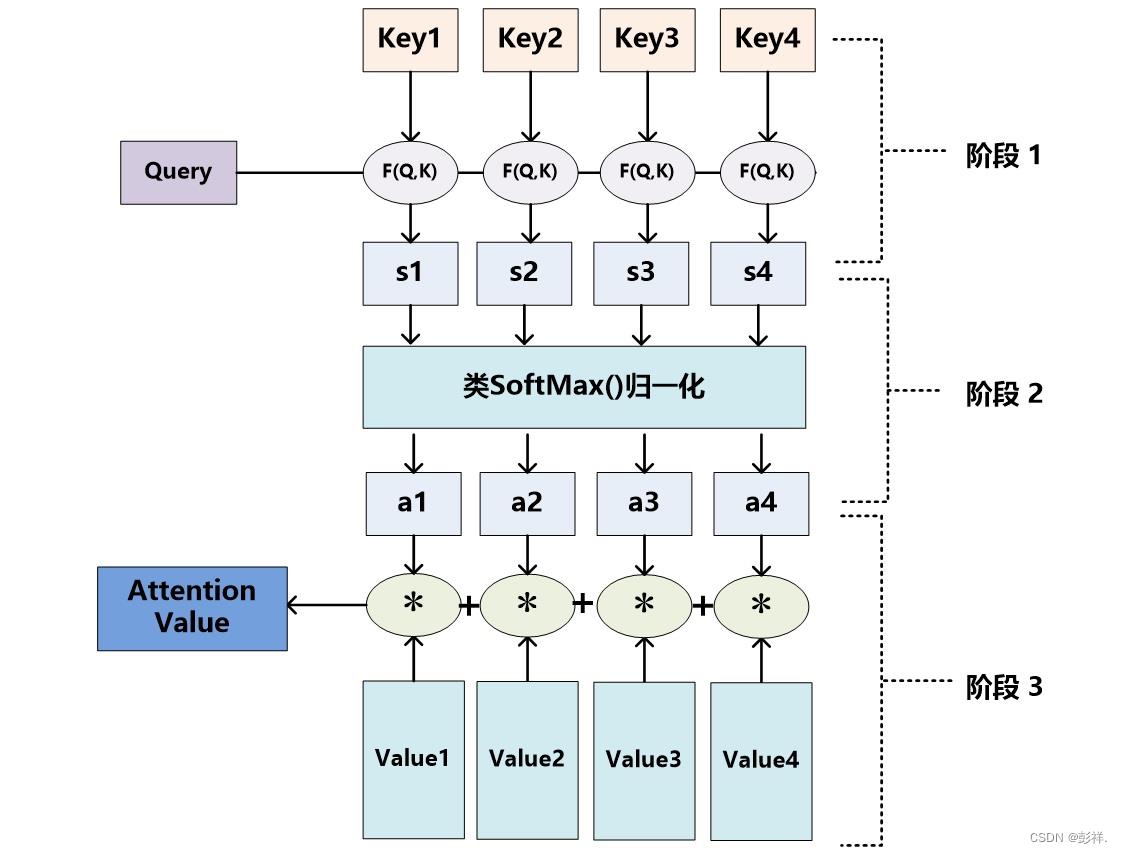
在第一个阶段，可以引入不同的函数和计算机制，根据Query和某个key_i，计算两者的相似性或者相关性，最常见的方法包括：求两者的向量点积、求两者的向量Cosine相似性或者通过再引入额外的神经网络来求值，即如下方式：

第一阶段产生的分值根据具体产生的方法不同其数值取值范围也不一样，第二阶段引入类似SoftMax的计算方式对第一阶段的得分进行数值转换，一方面可以进行归一化，将原始计算分值整理成所有元素权重之和为1的概率分布；另一方面也可以通过SoftMax的内在机制更加突出重要元素的权重。即一般采用如下公式计算：

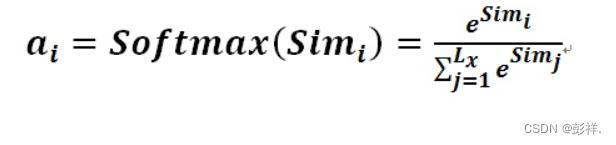
第二阶段的计算结果a即为value对应的权重系数，然后进行加权求和即可得到Attention数值：

通过如上三个阶段的计算，即可求出针对Query的Attention数值，目前绝大多数具体的注意力机制计算方法都符合上述的三阶段抽象计算过程。

query 、 key & value 的概念其实来源于推荐系统。基本原理是：给定一个 query，计算query 与 key 的相关性，然后根据query 与 key 的相关性去找到最合适的 value。举个例子：在电影推荐中。query 是某个人对电影的喜好信息（比如兴趣点、年龄、性别等）、key 是电影的类型（喜剧、年代等）、value 就是待推荐的电影。在这个例子中，query, key 和 value 的每个属性虽然在不同的空间，其实他们是有一定的潜在关系的，也就是说通过某种变换，可以使得三者的属性在一个相近的空间中。

1. self-attention 之所以取推荐系统中的 query、key 、value三个概念，就是利用了与推荐系统相似的流程。但是 self-attention 不是为了 query 去找 value，而是根据当前 query 获取 value 的加权和。这是 self-attention 的任务使然，想要为当前输入找到一个更好的加权输出，该输出要包含所有可见的输入序列信息，而注意力就是通过权重来控制。

2. self-attention 中这里 key 和 value 都是输入序列本身的一个变换，可能这也是 self-attention 的另外一层含义吧：自身同时作为 key 和 value。其实也非常合理，因为在推荐系统中，虽然 key 和 value 属性原始的特征空间不同，但是它们是有强关联关系的，因此他们通过一定的空间变换，是可以统一到一个特征空间中。这也是为什么self-attention 要乘以 W 的原因之一。

建立注意力模型

注意力机制在神经网络中的实现方式如下：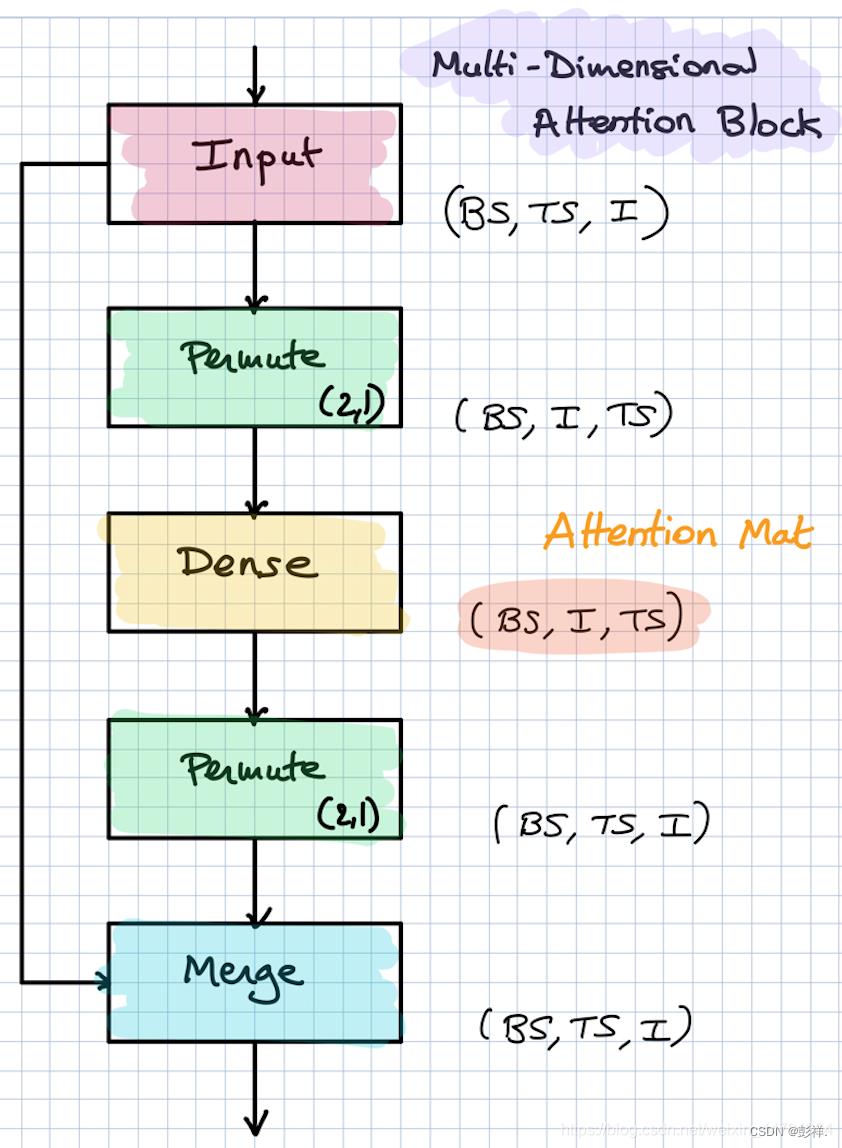
我们将一串时间序列传入到LSTM中，可以获得一个维度为(batch_size, time_steps, lstm_units)的输出，我们可以把其当作每一个时间节点的特征，我们把这样的一个输出作为上述图片的Input。

经过Permute将2、1轴翻转后，其维度从(batch_size, time_steps, lstm_units)转化成(batch_size, lstm_units, time_steps)。

再经过一个全连接层和Softmax后，其维度仍为(batch_size, lstm_units, time_steps)，其实际内涵为，利用全连接层计算每一个time_steps的权重。

再经过Permute将2、1轴翻转后，其维度从(batch_size, lstm_units, time_steps)转化成(batch_size, time_steps, lstm_units)。代表每一个STEP中每一个特征的权重。

最后将这个结果与Input相乘，也就是将每个STEP的权重，乘上他们的特征。
能够获取每个STEP之间的联系。

代码实现

    #   注意力模块，主要是实现对step维度的注意力机制
    #   在这里大家可能会疑惑，为什么需要先Permute再进行注意力机制的施加。
    #   这是因为，如果我们直接进行全连接的话，我们的最后一维是特征维度，这个时候，我们每个step的特征是分开的，
    #   此时进行全连接的话，得出来注意力权值每一个step之间是不存在特征交换的，自然也就不准确了。
    #   所以在这里我们需要首先将step维度转到最后一维，然后再进行全连接，根据每一个step的特征获得注意力机制的权值。
    def attention_block(self,inputs,time_step):
        # batch_size, time_steps, lstm_units -> batch_size, lstm_units, time_steps
        a = Permute((2, 1))(inputs)
        # batch_size, lstm_units, time_steps -> batch_size, lstm_units, time_steps
        a = Dense(time_step, activation='softmax')(a)#和步长有关
        # batch_size, lstm_units, time_steps -> batch_size, time_steps, lstm_units
        a_probs = Permute((2, 1), name='attention_vec')(a)
        # 相当于获得每一个step中，每个特征的权重
        output_attention_mul = merge([inputs, a_probs], name='attention_mul', mode='mul')
        return output_attention_mul

神经网络模型调用

 def generate_attention_model(self, n_input, n_out, n_features):
        inputs = Input(shape=(n_input, n_features,))
        # (batch_size, time_steps, input_dim) -> (batch_size, input_dim, lstm_units)
        lstm_out = LSTM(50, return_sequences=True)(inputs)
        attention_mul = self.attention_block(lstm_out,n_input)
        # (batch_size, input_dim, lstm_units) -> (batch_size, input_dim*lstm_units)
        attention_mul = Flatten()(attention_mul)
        output = Dense(n_out, activation='sigmoid')(attention_mul)
        model = Model(inputs=[inputs], outputs=output)
        model.summary()
        model.compile(loss="mse", optimizer='adam')
        return model

LSTM+Attention

这里使用的是LSTM+Attention模型结构
LSTM内部有Gate机制，其中input gate选择哪些当前信息进行输入，forget gate选择遗忘哪些过去信息，我觉得这算是一定程度的Attention了，而且号称可以解决长期依赖问题，实际上LSTM需要一步一步去捕捉序列信息，在长文本上的表现是会随着step增加而慢慢衰减，难以保留全部的有用信息。
LSTM通常需要得到一个向量，再去做任务，常用方式有：
a. 直接使用最后的hidden state（可能会损失一定的前文信息，难以表达全文）
b. 对所有step下的hidden state进行等权平均（对所有step一视同仁）。
c. Attention机制，对所有step的hidden state进行加权，把注意力集中到整段文本中比较重要的hidden state信息。性能比前面a，b 两种要好一点，而方便可视化观察哪些step是重要的，但是要小心过拟合，而且也增加了计算量。
我们这里使用的也是第三种。