文献阅读17期：Deep Learning on Graphs: A Survey - 6

Posted 2022-11-23 RaZLeon

[ 文献阅读·综述 ] Deep Learning on Graphs: A Survey [1]

推荐理由：图神经网络的survey paper，在很多的领域展现出了独特的作用力，分别通过GRAPH RNN（图循环网络）、GCN（图卷积）、GRAPH AUTOENCODERS（图自编码器）、GRAPH REINFORCEMENT LEARNING（图强化学习模型）、GRAPH ADVERSARIAL METHODS（图对抗模型）等五个类型的模型进行阐述，可以让大家对图神经网络有一个整体的认识。

6.图强化学习

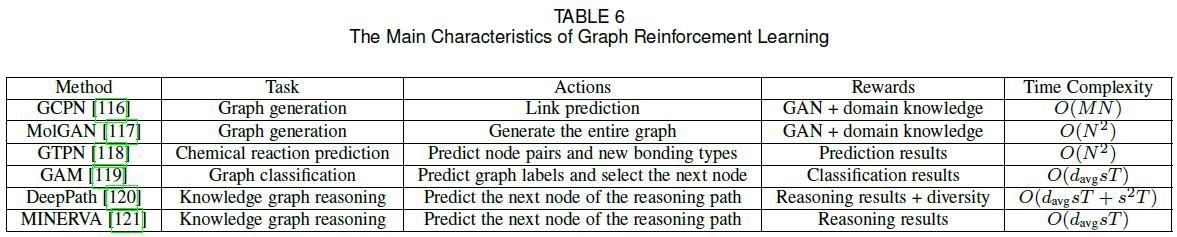
• 深度学习的一个尚未讨论的方面是强化学习（RL），它已被证明在人工智能任务（如玩游戏）中有效。RL擅长从反馈中学习，特别是在处理不可微目标和约束时。在本节中，我们将回顾图RL方法。表6总结了它们的主要特点。
• GCPN利用RL生成目标导向的分子图，同时考虑非微分目标和约束条件。具体地说，图生成被建模为一个添加节点和边的Markov决策过程，生成模型被看作是一个在图生成环境中运行的RL代理。通过将代理操作视为链接预测，使用特定域和对抗性奖励，并使用GCN学习节点表示，GCPN可以使用策略梯度以端到端的方式进行训练。
• 一个并行的工作，MolGAN，采用了类似的想法，使用RL生成分子图。然而，与其通过一系列动作生成图形，其建议直接生成完整的图形；这种方法对小分子特别有效。
• GTPN采用RL预测化学反应产物。具体来说，该代理在分子图中选择节点对并预测其新的键合类型，并根据预测是否正确立即和最后给予奖励。GTPN使用GCN学习节点表示，使用RNN记忆预测序列。
• GAM利用随机游动将RL应用于图形分类。作者将随机游动的产生建模为部分可观测马尔可夫决策过程（POMDP）。代理执行两个操作：首先，它预测图的标签；然后，它在随机游走中选择下一个节点。奖励仅取决于代理是否正确地对图进行分类，即：
  $$\mathcal{J}(\theta )={\mathbb{E}}_{P\left(S_{1:T};\theta \right)}\sum _{t=1}^T{r}_t\text{\hspace{1em}(60)}$$
• DeepPath和MINERVA都采用RL进行知识图推理。具体来说，DeepPath的目标是寻路，即在两个目标节点之间找到信息量最大的路径，而MINERVA则负责问答任务，即在给定问题节点和关系的情况下找到正确的答案节点。在这两种方法中，RL代理需要在每一步预测路径中的下一个节点，并以KG为单位输出推理路径。如果路径到达正确的目的地，代理将获得奖励。DeepPath还添加了一个正则化项来鼓励路径多样性。

7.图对抗方法

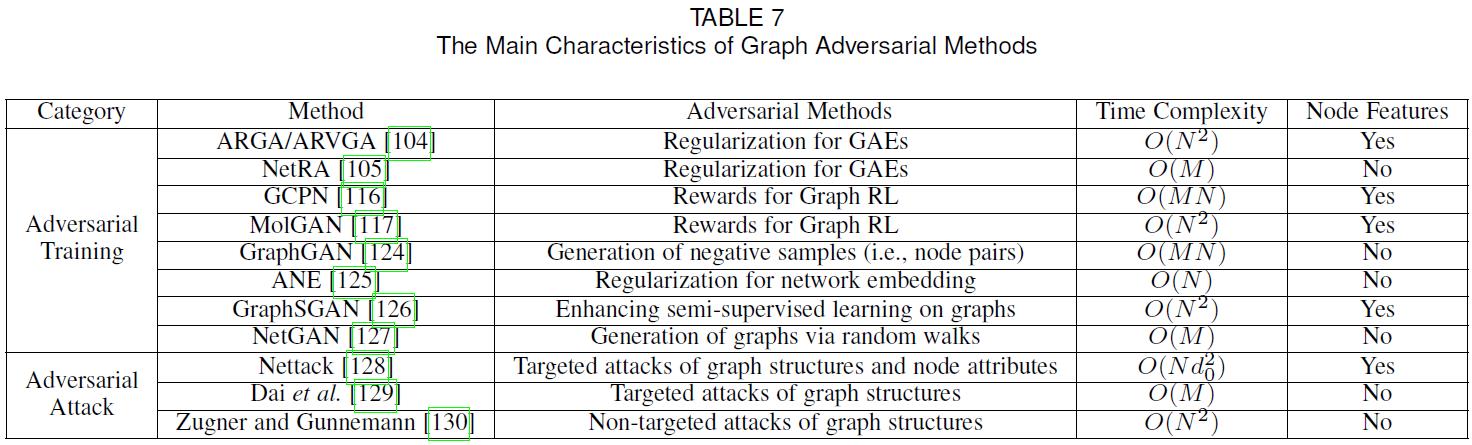
• 近年来，在机器学习领域，诸如GANs和敌对攻击等对抗性方法越来越受到人们的关注。在本节中，我们将回顾如何将对抗性方法应用于图。表7总结了图形对抗方法的主要特点。

7.1.对抗训练

• GAN背后的基本思想是建立两个链接模型：鉴别器和生成器。生成器的目标是通过生成假数据来“欺骗”鉴别器，而鉴别器的目标是区分样本是来自真实数据还是由生成器生成的。随后，两个模型通过使用minimax博弈进行联合训练，从中受益。对抗训练在生成模型和提高判别模型的泛化能力方面都是有效的。在第5.3.1节和第6节中，我们分别回顾了如何在GAEs和图RL中使用对抗性训练方案。在这里，我们详细回顾了其他几种图形对抗训练方法。
• GraphGAN建议使用GAN来增强具有以下目标函数的图嵌入方法：
  $$\begin{array}{rl}\underset{\mathcal{G}}{\min }\underset{\mathcal{D}}{\max }\sum _{i=1}^N& ({\mathbb{E}}_{v\sim p_{\text{graph }}\left(\cdot \mid v_i\right)}\left[\log \mathcal{D}\left(v,v_i\right)\right]\\ & +{\mathbb{E}}_{v\sim \mathcal{G}\left(\cdot \mid v_i\right)}\left[\log \left(1-\mathcal{D}\left(v,v_i\right)\right)\right])\end{array}\text{\hspace{1em}(61)}$$
  其中：
  $$\mathcal{D}\left(v,v_i\right)=\sigma \left({\mathbf{d}}_v{\mathbf{d}}_{v_i}^T\right),\mathcal{G}\left(v\mid v_i\right)=\frac{\exp \left({\mathbf{g}}_v{\mathbf{g}}_{v_i}^T\right)}{{\sum }_{v^{\prime }\ne v_i}\exp \left({\mathbf{g}}_{v^{\prime }}{\mathbf{g}}_{v_i}^T\right)}\text{\hspace{1em}(62)}$$
• Nettack首先通过修改图结构和节点属性提出了攻击节点分类模型，如GCNs。
  argmax ⁡ ( A ′ , F V ) ∈ P max ⁡ c ≠ c t r u e log ⁡ Z v 0 , c ∗ − log ⁡ Z v 0 , c t r u e ∗  s.t.  Z ∗ = F θ ∗ ( A ′ , F V ′ ) , θ ∗ = argmin ⁡ θ L F ( A ′ , F V ′ ) , (63) \\beginaligned &\\underset\\left(\\mathbfA^\\prime, \\mathbfF^V\\right) \\in \\mathcalP\\operatornameargmax \\max _c \\neq c_t r u e \\log \\mathbfZ_v_0, c^*-\\log \\mathbfZ_v_0, c_t r u e^* \\\\ &\\text s.t. \\mathbfZ^*=\\mathcalF_\\theta^*\\left(\\mathbfA^\\prime, \\mathbfF^V \\prime\\right), \\theta^*=\\operatornameargmin_\\theta \\mathcalL_\\mathcalF\\left(\\mathbfA^\\prime, \\mathbfF^V \\prime\\right), \\endaligned\\tag63 ​(A′,FV)∈Pargmax​c​=ctrue​max​logZv0​,c∗​−logZv0​,ctrue​∗​ s.t. Z∗=F文献阅读17期：Deep Learning on Graphs: A Survey - 6

  文献阅读16期：Deep Learning on Graphs: A Survey - 5

  文献阅读12期：Deep Learning on Graphs: A Survey - 1

  文献阅读15期：Deep Learning on Graphs: A Survey - 4

  文献阅读14期：Deep Learning on Graphs: A Survey - 3

  文献阅读13期：Deep Learning on Graphs: A Survey - 2