特征选择方法之主成分分析

Posted 2022-11-23 彭祥.

为什么要进行特征选择？

目前在做疫情数据预测，在所得的疫情数据集中有很多特征，那么这在涉及庞大的计算量的同时还会增加我们理解难度，那么我们就要从中选择出最具有代表性的几个特征，总的来说，进行特征选择的好处有：

降低复杂度：特征越小，我们耗费的计算时间也就越少。
降低噪音：比如说西瓜分类中，西瓜的id就毫无作用。
增加模型的可读性。

特征选择的方法有哪些？

我们主要是介绍一种名为主成分分析的特征选择方法，当前也会举其他简单案例来说明特征选择（降维）的作用和原理。

方差

很容易的理解，如果某一个特征的特征值都一样，或者说相互之间都很相似，那么我们可以理解为这个特征并没有提供什么有用的信息给我们，因此我们可以去掉这一个特征。那么如何判断是否特征值是否相似，emm，方差可以做到这个。
在scikit-learn中提供了VarianceThreshold转换器用来去除方差小于某一个阈值的列，具体的使用可以看官网。使用示例如下：

import numpy as np
X = np.arange(30).reshape((10, 3))

创建一个10行3列的矩阵

然后我们对矩阵进行更改，将第二列的所有值都设为1：

X[:,1] = 1

然后我们使用转换器对数据集进行处理：

from sklearn.feature_selection import VarianceThreshold
# threshold代表的就是阈值，默认是0.0
vt = VarianceThreshold(threshold=0.0)
Xt = vt.fit_transform(X)

我们可以看到第二列的已经被去除了。

在VarianceThreshold有两个重要的函数：fit 和 transform，fit 函数是去计算array的方差，而transform函数就是去转换array数组，将反差小于阈值的去除。
我们可以通过variances_去查看具体的方差是多少。

通过设置我们的阈值来去除相似性很高的数据。
这种方法是较为简单的。

PCA主成分分析法

主成分分析是利用降维的思想，在损失很少信息的前提下把多个指标转化为几个综合指标的多元统计方法。通常把转化生成的综合指标称之为主成分，其中每个主成分都是原始变量的线性组合，且各个主成分之间互不相关，这就使得主成分比原始变量具有某些更优越的性能。这样在研究复杂问题时就可以只考虑少数几个主成分而不至于损失太多信息，从而更容易抓住主要矛盾，揭示事物内部变量之间的规律性，同时使问题得到简化，提高分析效率。

分析步骤

主成分分析的步骤：

1.根据研究问题选取初始分析变量；
2.根据初始变量特性判断由协方差阵求主成分还是由相关阵求主成分（数据标准化的话需要用系数相关矩阵，数据未标准化则用协方差阵）；
3.求协差阵或相关阵的特征根与相应标准特征向量；
4.判断是否存在明显的多重共线性，若存在，则回到第一步；
5.主成分分析的适合性检验
6.得到主成分的表达式并确定主成分个数，选取主成分；
7.结合主成分对研究问题进行分析并深入研究。

注意事项

一组数据是否可以用主成分分析，必须做适合性检验。可以用球形检验和KMO统计量检验。

（1）球形检验（Bartlett)

球形检验的假设：
H0：相关系数矩阵为单位阵（即变量不相关）
H1：相关系数矩阵不是单位阵（即变量间有相关关系）
检验总体变量的相关矩阵是否是单位阵（相关系数矩阵对角线的所有元素均为1,所有非对角线上的元素均为零）；即检验各个变量是否各自独立。

# Bartlett's球状检验
from factor_analyzer.factor_analyzer import calculate_bartlett_sphericity
 
chi_square_value, p_value = calculate_bartlett_sphericity(df)
print(chi_square_value, p_value)

输出结果： 125572.36137229178 0.0

（2）KMO（Kaiser-Meyer-Olkin)统计量

KMO统计量比较样本相关系数与样本偏相关系数，它用于检验样本是否适于作主成分分析。
检查变量间的相关性和偏相关性，取值在0-1之间；KOM统计量越接近1，变量间的相关性越强，偏相关性越弱，因子分析的效果越好。

# 通常取值从0.6开始进行因子分析
from factor_analyzer.factor_analyzer import calculate_kmo
kmo_all, kmo_model = calculate_kmo(df)
print(kmo_all)

  KMO的值在0,1之间，该值越大，则样本数据越适合作主成分分析和因子分析
  。一般要求该值大于0.5，方可作主成分分析或者相关分析。
  Kaiser在1974年给出了经验原则：

            0.9以上       适合性很好

            0.8~0.9        适合性良好

            0.7~0.8        适合性中等

            0.6~0.7        适合性一般

            0.5~0.6        适合性不好

            0.5以下       不能接受的    

（3）主成分分析的逻辑框图

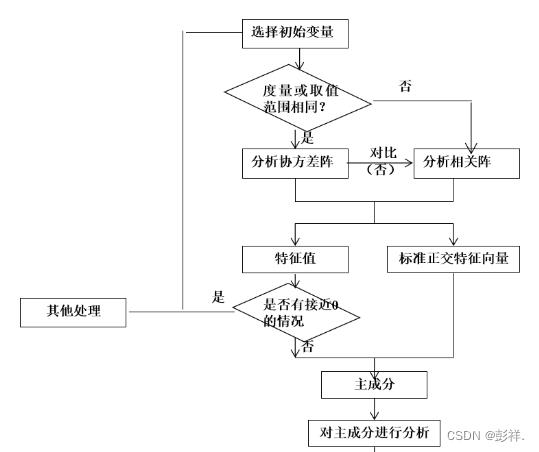
数据标准化做法

数据标准化

根据初始变量特性判断由协方差阵求主成分还是由相关阵求主成分（数据标准化的话需要用系数相关矩阵，数据未标准化则用协方差阵）；
用到了 preprocessing 库

from sklearn import preprocessing
df = preprocessing.scale(df)

求相关系数矩阵

为了方面下面引用，就和协方差阵的赋值符号一样了！

covX = np.around(np.corrcoef(df.T),decimals=3)

求解特征值和特征向量

featValue, featVec=  np.linalg.eig(covX.T)  #求解系数相关矩阵的特征值和特征向量
featValue, featVec

数据不标准化做法

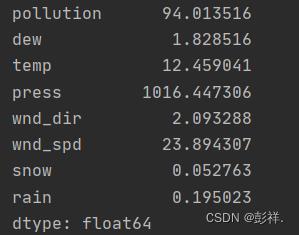
求均值

def meanX(dataX):
    return np.mean(dataX,axis=0)#axis=0表示依照列来求均值。假设输入list,则axis=1
average = meanX(df)

查看列数和行数

m, n = np.shape(df)

写出同数据集一样的均值矩阵

np.tile(a,(2,1))第一个参数为Y轴扩大倍数，第二个为X轴扩大倍数。本例中X轴扩大一倍便为不复制

data_adjust = []
avgs = np.tile(average, (m, 1))

对数据集进行去中心化

及矩阵数据与均值矩阵做差

data_adjust = df - avgs

计算协方差阵

协方差矩阵在统计学和机器学习中随处可见，一般而言，可视作方差和协方差两部分组成，即方差构成了对角线上的元素，协方差构成了非对角线上的元素。
在统计学中，方差是用来度量单个随机变量的离散程度，而协方差则一般用来刻画两个随机变量的相似程度，其中，方差的计算公式为：

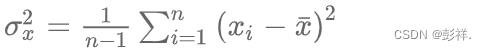
在此基础上，协方差的计算公式被定义为：

根据方差的定义，给定 d个随机变量 x_k ，则这些随机变量的方差为:

其中，为方便书写，X_ki 表示随机变量 X_k 中的第 i 个观测样本，n 表示样本量，每个随机变量所对应的观测样本数量均为 n 。
对于这些随机变量，我们还可以根据协方差的定义，求出两两之间的协方差，即:

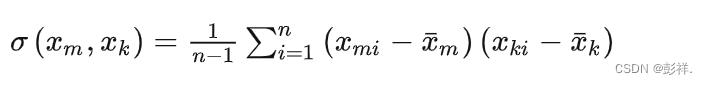
因此，协方差矩阵为:

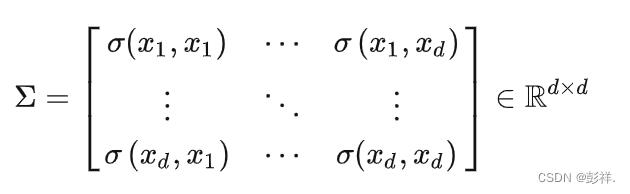
其中，对角线上的元素为各个随机变量的方差，非对角线上的元素为两两随机变量之间的协方差，根据协方差的定义，我们可以认定：其为对称矩阵(symmetric matrix)，其大小为 d*d

covX = np.cov(data_adjust.T)

可得其数值关于对角线对称。

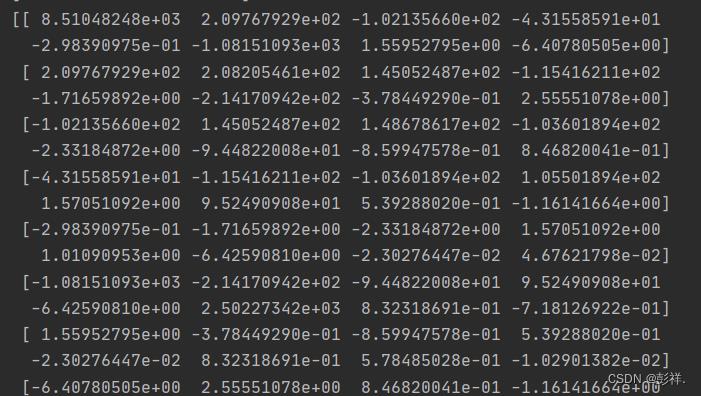
计算协方差阵的特征值和特征向量

Ax=cx：A为矩阵，c为特征值，x为特征向量。

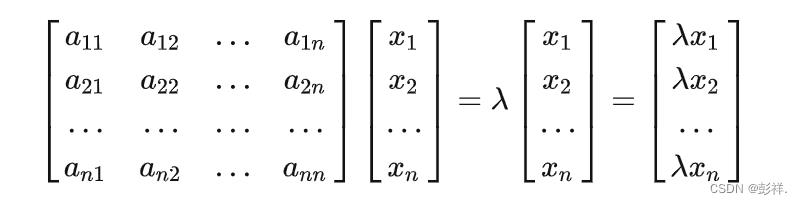
特征值分解可以得到特征值与特征向量，特征值表示的是这个特征到底有多重要，而特征向量表示这个特征是什么。
即不同的特征值，对应的特征向量便不同，在这里可认为有8个特征向量，则对应有8个特征值，其权值不同，即重要性不同。
比如新冠治疗中的瑞得西韦， 特征值就是该神药该服用多少？还有其它药方子，如莲花清瘟等，假设都能治疗新冠肺炎，但用量肯定是不一样的，即不同特征向量对应的特征值不一。

featValue, featVec=  np.linalg.eig(covX) 

特征值：

下面方法则不区分标准化或为标准化了

对特征值进行排序并输出 降序

featValue = sorted(featValue)[::-1]

[8707.400699078189, 2339.4220390797277, 378.53865993475847,
31.035420734473398, 18.91003460944435, 1.9209877821871622, 0.9437246988094519, 0.5654529260717821]

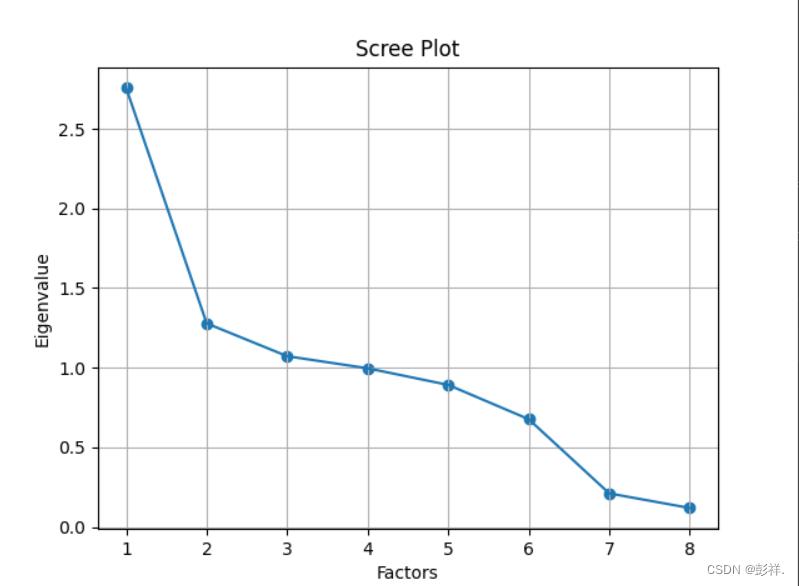
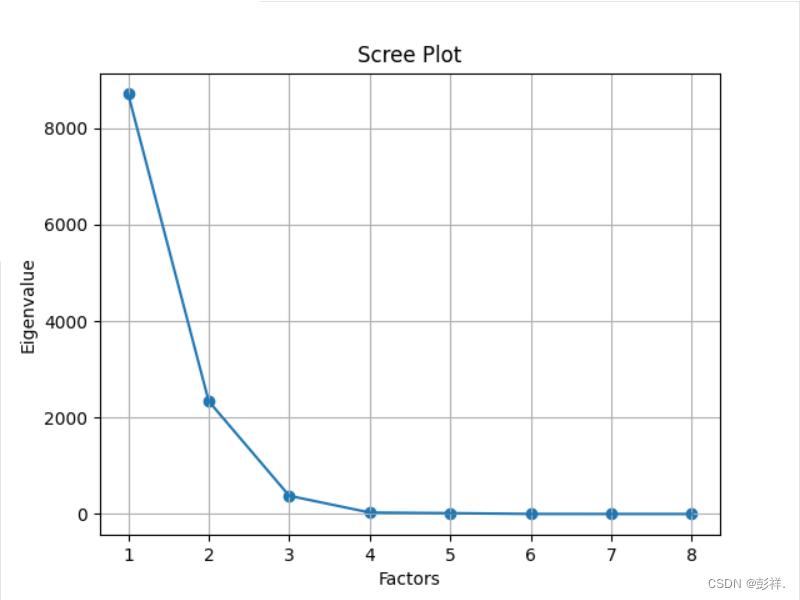
绘制散点图和折线图

# 同样的数据绘制散点图和折线图
plt.scatter(range(1, df.shape[1] + 1), featValue)
plt.plot(range(1, df.shape[1] + 1), featValue) 
# 显示图的标题和xy轴的名字
# 最好使用英文，中文可能乱码
plt.title("Scree Plot")  
plt.xlabel("Factors")
plt.ylabel("Eigenvalue") 
plt.grid()  # 显示网格
plt.show()  

标准化后的图表：

未标准化的图表：

求特征值的贡献度

gx = featValue/np.sum(featValue)

[7.58567836e-01 2.03804829e-01 3.29773789e-02 2.70373131e-03
1.64739680e-03 1.67351842e-04 8.22150292e-05 4.92609008e-05]

求特征值的累计贡献度

贡献率是我们选择主成分的依据，如需要累计贡献率达到90%,则若有2个符合，这也就是说明我们k=2，即选择两个特征值。

lg = np.cumsum(gx)

选出主成分

#选出主成分
k=[i for i in range(len(lg)) if lg[i]<0.85]
k = list(k)
print(k)

选出主成分对应的特征向量矩阵

selectVec = np.matrix(featVec.T[k]).T
selectVe=selectVec*(-1)

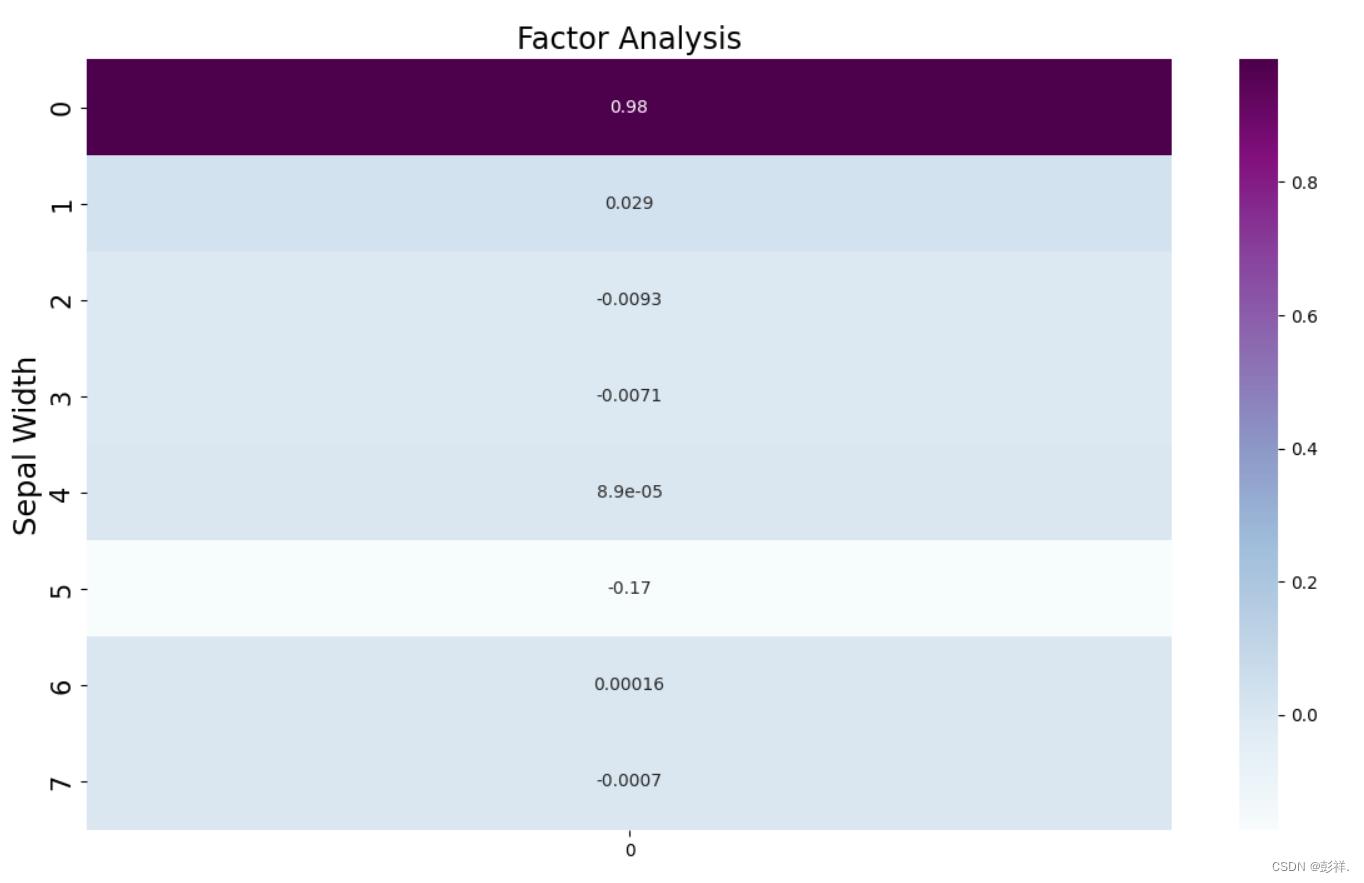
绘制热力图

# 绘图
 
plt.figure(figsize = (14,14))
ax = sns.heatmap(selectVec, annot=True, cmap="BuPu")
 
# 设置y轴字体大小
ax.yaxis.set_tick_params(labelsize=15)
plt.title("Factor Analysis", fontsize="xx-large")
 
# 设置y轴标签
plt.ylabel("Sepal Width", fontsize="xx-large")
# 显示图片
plt.show()
 
# 保存图片
# plt.savefig("factorAnalysis", dpi=500)