数据预处理-python实现
Posted 彭祥.
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了数据预处理-python实现相关的知识,希望对你有一定的参考价值。
首先是数据读取:格式主要有excel,csv,txt等
import pandas as pd
data = pd.read_csv(r'../filename.csv') #读取csv文件
data = pd.read_table(r'../filename.txt') #读取txt文件
data = pd.read_excel(r'../filename.xlsx') #读取excel文件
# 获取数据库中的数据
import pymysql
conn = pymysql.connect(host='localhost',user='root',passwd='12345',db='mydb') #连接数据库,注意修改成要连的数据库信息
cur = conn.cursor() #创建游标
cur.execute("select * from train_data limit 100") #train_data是要读取的数据名
data = cur.fetchall() #获取数据
cols = cur.description #获取列名
conn.commit() #执行
cur.close() #关闭游标
conn.close() #关闭数据库连接
col = []
for i in cols:
col.append(i[0])
data = list(map(list,data))
data = pd.DataFrame(data,columns=col)
数据读取完成后,可以查看数据内容
data.head() #显示前五行数据
data.tail() #显示末尾五行数据
data.info() #查看各字段的信息
data.shape #查看数据集有几行几列,data.shape[0]是行数,data.shape[1]是列数
data.describe() #查看数据的大体情况,均值,最值,分位数值...
data.columns.tolist() #得到列名的list
数据预处理的意义
数据处理相关的工作时间占据了整个项目的70%以上。数据的质量,直接决定了模型的预测和泛化能力的好坏。它涉及很多因素,包括:准确性、完整性、一致性、时效性、可信性和解释性。而在真实数据中,我们拿到的数据可能包含了大量的缺失值,可能包含大量的噪音,也可能因为人工录入错误导致有异常点存在,非常不利于算法模型的训练。数据清洗的结果是对各种脏数据进行对应方式的处理,得到标准的、干净的、连续的数据,提供给数据统计、数据挖掘等使用。
预处理方法介绍
数据预处理的主要步骤分为:数据清理、数据集成、数据规约和数据变换。
数据清理
数据清理(data cleaning) 的主要思想是通过填补缺失值、光滑噪声数据,平滑或删除离群点,并解决数据的不一致性来“清理“数据。如果用户认为数据时脏乱的,他们不太会相信基于这些数据的挖掘结果,即输出的结果是不可靠的。
1、缺失值的处理
由于现实世界中,获取信息和数据的过程中,会存在各类的原因导致数据丢失和空缺。
查看缺失值
print(data.isnull().sum()) #统计每列有几个缺失值
missing_col = data.columns[data.isnull().any()].tolist() #找出存在缺失值的列
import numpy as np
#统计每个变量的缺失值占比
def CountNA(data):
cols = data.columns.tolist() #cols为data的所有列名
n_df = data.shape[0] #n_df为数据的行数
for col in cols:
missing = np.count_nonzero(data[col].isnull().values) #col列中存在的缺失值个数
mis_perc = float(missing) / n_df * 100
print("col的缺失比例是miss%".format(col=col,miss=mis_perc))
当然有的算法(贝叶斯、xgboost、神经网络等)对缺失值不敏感,或者有些字段对结果分析作用不大,此时就没必要费时费力去处理缺失值啦
针对这些缺失值的处理方法,主要是基于变量的分布特性和变量的重要性(信息量和预测能力)采用不同的方法。主要分为以下几种:
删除变量:若变量的缺失率较高(大于80%),覆盖率较低,且重要性较低,可以直接将变量删除。
在数据量比较大时候或者一条记录中多个字段缺失,不方便填补的时候可以选择删除缺失值,指的是将该变量(特征)删除
data.dropna(axis=0,how="any",inplace=True) #axis=0代表'行','any'代表任何空值行,若是'all'则代表所有值都为空时,才删除该行
data.dropna(axis=0,inplace=True) #删除带有空值的行
data.dropna(axis=1,inplace=True) #删除带有空值的列
定值填充:工程中常见用-9999进行替代
data = data.fillna(0) #缺失值全部用0插补
data['col_name'] = data['col_name'].fillna('UNKNOWN') #某列缺失值用固定值插补
统计量填充:若缺失率较低(小于95%)且重要性较低,则根据数据分布的情况进行填充。对于数据符合均匀分布,用该变量的均值填补缺失,对于数据存在倾斜分布的情况,采用中位数进行填补。
出现最频繁值填充
即众数插补,离散/连续数据都行,适用于名义变量,如性别
freq_port = data.col_name.dropna().mode()[0] # mode返回出现最多的数据,col_name为列名
data['col_name'] = data['col_name'].fillna(freq_port) #采用出现最频繁的值插补
中位数/均值插补
data['col_name'].fillna(data['col_name'].dropna().median(),inplace=True) #中位数插补,适用于偏态分布或者有离群点的分布
data['col_name'].fillna(data['col_name'].dropna().mean(),inplace=True) #均值插补,适用于正态
插值法填充:包括随机插值,多重差补法,热平台插补,拉格朗日插值,牛顿插值等
拉格朗日插值法
一般针对有序的数据,如带有时间列的数据集,且缺失值为连续型数值小批量数据
from scipy.interpolate import lagrange
#自定义列向量插值函数,s为列向量,n为被插值的位置,k为取前后的数据个数,默认5
def ployinterp_columns(s, n, k=5):
y = s[list(range(n-k,n)) + list(range(n+1,n+1+k))] #取数
y = y[y.notnull()] #剔除空值
return lagrange(y.index, list(y))(n) #插值并返回插值结果
#逐个元素判断是否需要插值
for i in data.columns:
for j in range(len(data)):
if (data[i].isnull())[j]: #如果为空即插值
data[i][j] = ployinterp_columns(data[i],j)
模型填充:使用回归、贝叶斯、随机森林、决策树等模型对缺失数据进行预测。
哑变量填充:若变量是离散型,且不同值较少,可转换成哑变量,例如性别SEX变量,存在male,fameal,NA三个不同的值,可将该列转换成 IS_SEX_MALE, IS_SEX_FEMALE, IS_SEX_NA。若某个变量存在十几个不同的值,可根据每个值的频数,将频数较小的值归为一类’other’,降低维度。此做法可最大化保留变量的信息。
总结来看,常用的做法是:先用pandas.isnull.sum()检测出变量的缺失比例,考虑删除或者填充,若需要填充的变量是连续型,一般采用均值法和随机差值进行填充,若变量是离散型,通常采用中位数或哑变量进行填充。
注意:若对变量进行分箱离散化,一般会将缺失值单独作为一个箱子(离散变量的一个值)
2、噪声处理
噪声是变量的随机误差和方差,是观测点和真实点之间的误差,即偏差则是度量算法的期望输出与真实标记的区别,表达了学习算法对数据的拟合能力。而噪声则表示数据的真实标记与数据在数据集上标记的区别,表明算法在当前任务上能达到的测试误差的下界。
假设数据集用D 表示,测试样本x,y 表示x 在数据集上的标记,
y
‾
\\overline\\texty
y 表示x 的真实标记,f ( x ; D )表示从训练集D上学得的模型 f 的预测输出。令
f(x)
‾
\\overline\\textf(x)
f(x)表示从不同训练集上学得模型的期望输出,则
f(x) ‾ \\overline\\textf(x) f(x) = E D [ f ( x ; D ) ]
则可以定义方差、偏差和噪声的表达,
方差为:
var(x)=E D [ (f(x;D)− f(x) ) 2 ]
偏差为:
bias2( x ) = [ f(x) ‾ \\overline\\textf(x) f(x) − y ‾ \\overline\\texty y ] 2
噪声为:
ϵ2 = E D [ (
y
‾
\\overline\\texty
y − y ) 2 ]
如果对期望泛化误差进行分解,可以得到:
E ( f ; D ) = bias2 ( x ) + v a r ( x ) + ϵ2
即算法的期望泛化误差可以分解为偏差、方差和噪声之和。
通常的处理办法:对数据进行分箱操作,等频或等宽分箱,然后用每个箱的平均数,中位数或者边界值(不同数据分布,处理方法不同)代替箱中所有的数,起到平滑数据的作用。另外一种做法是,建立该变量和预测变量的回归模型,根据回归系数和预测变量,反解出自变量的近似值。
3、离群点处理
异常值是数据分布的常态,处于特定分布区域或范围之外的数据通常被定义为异常或噪声。异常分为两种:“伪异常”,由于特定的业务运营动作产生,是正常反应业务的状态,而不是数据本身的异常;“真异常”,不是由于特定的业务运营动作产生,而是数据本身分布异常,即离群点。主要有以下检测离群点的方法:
简单统计分析:根据箱线图、各分位点判断是否存在异常,例如pandas的describe函数可以快速发现异常值。
基于绝对离差中位数(MAD):这是一种稳健对抗离群数据的距离值方法,采用计算各观测值与平均值的距离总和的方法。放大了离群值的影响。
基于距离:通过定义对象之间的临近性度量,根据距离判断异常对象是否远离其他对象,缺点是计算复杂度较高,不适用于大数据集和存在不同密度区域的数据集
基于密度:离群点的局部密度显著低于大部分近邻点,适用于非均匀的数据集
基于聚类:利用聚类算法,丢弃远离其他簇的小簇。
总结来看,在数据处理阶段将离群点作为影响数据质量的异常点考虑,而不是作为通常所说的异常检测目标点,因而一般采用较为简单直观的方法,结合箱线图和MAD的统计方法判断变量的离群点。
具体的处理手段:
根据异常点的数量和影响,考虑是否将该条记录删除,信息损失多
若对数据做了log-scale 对数变换后消除了异常值,则此方法生效,且不损失信息
平均值或中位数替代异常点,简单高效,信息的损失较少
在训练树模型时,树模型对离群点的鲁棒性较高,无信息损失,不影响模型训练效果
数据集成
数据分析任务多半涉及数据集成。数据集成将多个数据源中的数据结合成、存放在一个一致的数据存储,如数据仓库中。这些源可能包括多个数据库、数据方或一般文件。
实体识别问题:例如,数据分析者或计算机如何才能确信一个数 据库中的 customer_id 和另一个数据库中的 cust_number 指的是同一实体?通常,数据库和数据仓库 有元数据——关于数据的数据。这种元数据可以帮助避免模式集成中的错误。
冗余问题。一个属性是冗余的,如果它能由另一个表“导出”;如年薪。属性或 维命名的不一致也可能导致数据集中的冗余。 用相关性检测冗余:数值型变量可计算相关系数矩阵,标称型变量可计算卡方检验。
数据值的冲突和处理:不同数据源,在统一合并时,保持规范化,去重。
代码举例
CSV文件合并,这是数据集成的一个方式
实际数据可能分布在一个个的小的csv或者txt文档,而建模分析时可能需要读取所有数据,这时呢,需要将一个个小的文档合并到一个文件中:
#合并多个csv文件成一个文件
import glob
#合并
def hebing():
csv_list = glob.glob('*.csv') #查看同文件夹下的csv文件数
print(u'共发现%s个CSV文件'% len(csv_list))
print(u'正在处理............')
for i in csv_list: #循环读取同文件夹下的csv文件
fr = open(i,'rb').read()
with open('result.csv','ab') as f: #将结果保存为result.csv
f.write(fr)
print(u'合并完毕!')
#去重
def quchong(file):
df = pd.read_csv(file,header=0)
datalist = df.drop_duplicates()
datalist.to_csv(file)
if __name__ == '__main__':
hebing()
quchong("result.csv.csv")
数据规约
数据归约技术可以用来得到数据集的归约表示,它小得多,但仍接近地保持原数据的完整性。 这样,在归约后的数据集上挖掘将更有效,并产生相同(或几乎相同)的分析结果。一般有如下策略:
1、维度规约
用于数据分析的数据可能包含数以百计的属性,其中大部分属性与挖掘任务不相关,是冗余的。维度归约通过删除不相关的属性,来减少数据量,并保证信息的损失最小。
属性子集选择:目标是找出最小属性集,使得数据类的概率分布尽可能地接近使用所有属性的原分布。在压缩 的属性集上挖掘还有其它的优点。它减少了出现在发现模式上的属性的数目,使得模式更易于理解。
逐步向前选择:该过程由空属性集开始,选择原属性集中最好的属性,并将它添加到该集合中。在其后的每一次迭代,将原属性集剩下的属性中的最好的属性添加到该集合中。
逐步向后删除:该过程由整个属性集开始。在每一步,删除掉尚在属性集中的最坏属性。
向前选择和向后删除的结合:向前选择和向后删除方法可以结合在一起,每一步选择一个最 好的属性,并在剩余属性中删除一个最坏的属性。
python scikit-learn 中的递归特征消除算法Recursive feature elimination (RFE),就是利用这样的思想进行特征子集筛选的,一般考虑建立SVM或回归模型。
单变量重要性:分析单变量和目标变量的相关性,删除预测能力较低的变量。这种方法不同于属性子集选择,通常从统计学和信息的角度去分析。
pearson相关系数和卡方检验,分析目标变量和单变量的相关性。
回归系数:训练线性回归或逻辑回归,提取每个变量的表决系数,进行重要性排序。
树模型的Gini指数:训练决策树模型,提取每个变量的重要度,即Gini指数进行排序。
Lasso正则化:训练回归模型时,加入L1正则化参数,将特征向量稀疏化。
IV指标:风控模型中,通常求解每个变量的IV值,来定义变量的重要度,一般将阀值设定在0.02以上。
以上提到的方法,没有讲解具体的理论知识和实现方法,需要自己去熟悉掌握。通常的做法是根据业务需求来定,如果基于业务的用户或商品特征,需要较多的解释性,考虑采用统计上的一些方法,如变量的分布曲线,直方图等,再计算相关性指标,最后去考虑一些模型方法。如果建模需要,则通常采用模型方法去筛选特征,如果用一些更为复杂的GBDT,DNN等模型,建议不做特征选择,而做特征交叉。
2、维度变换:
维度变换是将现有数据降低到更小的维度,尽量保证数据信息的完整性。这里介绍常用的几种有损失的维度变换方法,将大大地提高实践中建模的效率
主成分分析(PCA)和因子分析(FA):PCA通过空间映射的方式,将当前维度映射到更低的维度,使得每个变量在新空间的方差最大。FA则是找到当前特征向量的公因子(维度更小),用公因子的线性组合来描述当前的特征向量。
奇异值分解(SVD):SVD的降维可解释性较低,且计算量比PCA大,一般用在稀疏矩阵上降维,例如图片压缩,推荐系统。
聚类:将某一类具有相似性的特征聚到单个变量,从而大大降低维度。
线性组合:将多个变量做线性回归,根据每个变量的表决系数,赋予变量权重,可将该类变量根据权重组合成一个变量。
数据变换
数据变换包括对数据进行规范化,离散化,稀疏化处理,达到适用于挖掘的目的。
1、规范化处理
数据中不同特征的量纲可能不一致,数值间的差别可能很大,不进行处理可能会影响到数据分析的结果,因此,需要对数据按照一定比例进行缩放,使之落在一个特定的区域,便于进行综合分析。特别是基于距离的挖掘方法,聚类,KNN,SVM一定要做规范化处理。
最大 - 最小规范化:将数据映射到[0,1]区间,
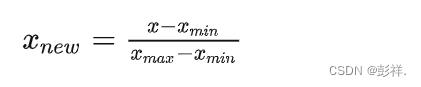
from sklearn.preprocessing import MinMaxScaler
x_scaler = MinMaxScaler()
y_scaler = MinMaxScaler()
#特征归一化
x_train_sca = x_scaler.fit_transform(X_train)
x_test_sca = x_scaler.transform(X_test)
y_train_sca = y_scaler.fit_transform(pd.DataFrame(y_train))
Z-Score标准化:处理后的数据均值为0,方差为1,
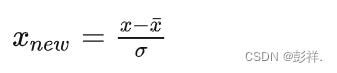
from sklearn.preprocessing import StandardScaler
#一般把train和test集放在一起做标准化,或者在train集上做标准化后,用同样的标准化器去标准化test集
scaler = StandardScaler()
train = scaler.fit_transform(train)
test = scaler.transform(test)
Log变换:在时间序列数据中,对于数据量级相差较大的变量,通常做Log函数的变换,
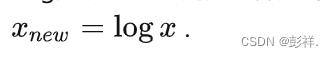
大多数机器学习算法中,会选择StandardScaler来进行特征缩放,因为MinMaxScaler对异常值非常敏感。在PCA,聚类,逻辑回归,支持向量机,神经网络这些算法中StandardScaler往往是最好的选择。
MinMaxScaler在不涉及距离度量、梯度、协方差计算以及数据需要被压缩到特定区间时使用广泛,比如数字图像处理中量化像素强度时,都会使用MinMaxScaler将数据压缩于[0,1]区间之中。
建议先试试看StandardScaler,效果不好换MinMaxScaler。
2、离散化处理
数据离散化是指将连续的数据进行分段,使其变为一段段离散化的区间。分段的原则有基于等距离、等频率或优化的方法。数据离散化的原因主要有以下几点:
模型需要:比如决策树、朴素贝叶斯等算法,都是基于离散型的数据展开的。如果要使用该类算法,必须将离散型的数据进行。有效的离散化能减小算法的时间和空间开销,提高系统对样本的分类聚类能力和抗噪声能力。离散化的特征相对于连续型特征更易理解。可以有效的克服数据中隐藏的缺陷,使模型结果更加稳定。
等频法:使得每个箱中的样本数量相等,例如总样本n=100,分成k=5个箱,则分箱原则是保证落入每个箱的样本量=20。
等宽法:使得属性的箱宽度相等,例如年龄变量(0-100之间),可分成 [0,20],[20,40],[40,60],[60,80],[80,100]五个等宽的箱。
聚类法:根据聚类出来的簇,每个簇中的数据为一个箱,簇的数量模型给定。
3、稀疏化处理
针对离散型且标称变量,无法进行有序的LabelEncoder时,通常考虑将变量做0,1哑变量的稀疏化处理,例如动物类型变量中含有猫,狗,猪,羊四个不同值,将该变量转换成is_猪,is_猫,is_狗,is_羊四个哑变量。若是变量的不同值较多,则根据频数,将出现次数较少的值统一归为一类’rare’。稀疏化处理既有利于模型快速收敛,又能提升模型的抗噪能力。
哑变量与独热编码


关于分箱操作
分箱就是把数据按特定的规则进行分组,实现数据的离散化,增强数据稳定性,减少过拟合风险。逻辑回归中进行分箱是非常必要的,其他树模型可以不进行分箱。
数据分箱(Binning)作为数据预处理的一部分,也被称为离散分箱或数据分段。其实分箱的概念其实很好理解,它的本质上就是把数据进行分组。
我们以年龄为例,看下面的表格,左边是原始年龄数据,右边是分箱后的数据:
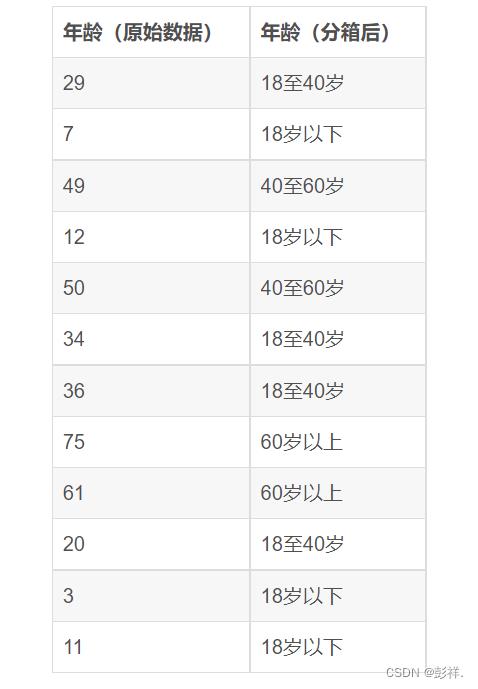
这里补充一句,虽然在实际建模中,分箱一般都是针对连续型数据(如价格、销量、年龄)进行的。但是从理论上,分箱也可以对分类型数据进行。比如,有些分类型数据可取的值非常多,像中国的城市这种数据,这种情况下可以通过分箱,让已经是离散型的数据变得更加离散,比如,城市可以被划分为一级城市、二级城市、三级城市,或者把垃圾分为有害垃圾、可回收垃圾、湿垃圾、干垃圾等等。
其他处理
描述性变量转换为数值型
大部分机器学习算法要求输入的数据必须是数字,不能是字符串,这就要求将数据中的描述性变量(如性别)转换为数值型数据
#寻找描述变量,并将其存储到cat_vars这个list中去
cat_vars = []
print('\\n描述变量有:')
cols = data.columns.tolist()
for col in cols:
if data[col].dtype == 'object':
print(col)
cat_vars.append(col)
##若变量是有序的##
print('\\n开始转换描述变量...')
from sklearn import preprocessing
le = preprocessing.LabelEncoder()
#将描述变量自动转换为数值型变量,并将转换后的数据附加到原始数据上
for col in cat_vars:
tran = le.fit_transform(data[col].tolist())
tran_df = pd.DataFrame(tran,columns=['num_'+col])
print('col经过转化为num_col'.format(col=col,num_col='num_'+col))
data = pd.concat([data, tran_df], axis=1)
del data[col] #删除原来的列
##若变量是无序变量##
#值得注意的是one-hot可能引发维度爆炸
for col in cat_vars:
onehot_tran = pd.get_dummies(data.col)
data = data.join(onehot_tran) #将one-hot后的数据添加到data中
del data[col] #删除原来的列
以上是关于数据预处理-python实现的主要内容,如果未能解决你的问题,请参考以下文章