支持向量机-Support Vector Machine

Posted 2022-11-22 dqhl1990

支持向量机-Support Vector Machine

---

将在SVM之前

初窥SVM，没想到其涉及了诸多最优化问题的内容，特此在理解SVM的同时，整理了会用到的最优化相关知识，都在这里了。

关于SVM的讲解，我看到了两种方法。一种是网上最多的最优超平面方法求解；另一种是Andrew Ng在Coursera上通过逻辑回归延伸出来的方法。这里我先整理根据网上看到的方法。

1. 什么是超平面？

维基百科上讲：在几何学中，一个超平面，是一个比它所在环境空间维度小1的子空间(余维度为1)。例如，三维空间的超平面是一个二维平面，二维空间的超平面是一个一维线。

对于$n$维空间，其内的超平面为：
$$w_1{x}_1+w_2{x}_2+\cdots +w_n{x}_n=b\text{\hspace{1em}(1.1)}$$定义的子集$X$，其中$w_1,w_2,\dots ,w_n$为不全为0的常数，并且为该超平面的法向量。

超平面将其所在的空间分成了两个部分，分别对应的是：

$$\begin{gathered} w_1{x}_1+w_2{x}_2+\cdots +w_n{x}_n>b \\ and \\ {w}_1{x}_1+w_2{x}_2+\cdots +w_n{x}_n<b \end{gathered}$$

用向量形式表示超平面公式为：
$$\begin{gathered} x=(x_1,x_2,\dots ,x_n{)}^T \\ w=(w_1,w_2,\dots ,w_n{)}^T \\ {w}^{T}x+b=0\text{\hspace{1em}(1.2)} \end{gathered}$$

其同样可以用不等式将所在的空间分成两部分：
$$\begin{gathered} w^{T}x+b>0 \\ and \\ {w}^{T}x+b<0 \end{gathered}$$
以二维空间为例，如图能直观地看出超平面（线）将二维平面分成了两部分：

问题定义

在进行推导之前，我们想对问题进行定义。假设给定一个特征空间上的训练数据集
$$T=(x_1,y_x),(x_2,y_2),\dots ,(x_n,y_n)$$其中，$x_i\in {\mathbb{R}}^n,y_i\in +1,-1,i=1,2,\dots ,n$。
我们的问题就是要找到空间中的一个超平面，能够最优的将不同类别的样本区分开来。

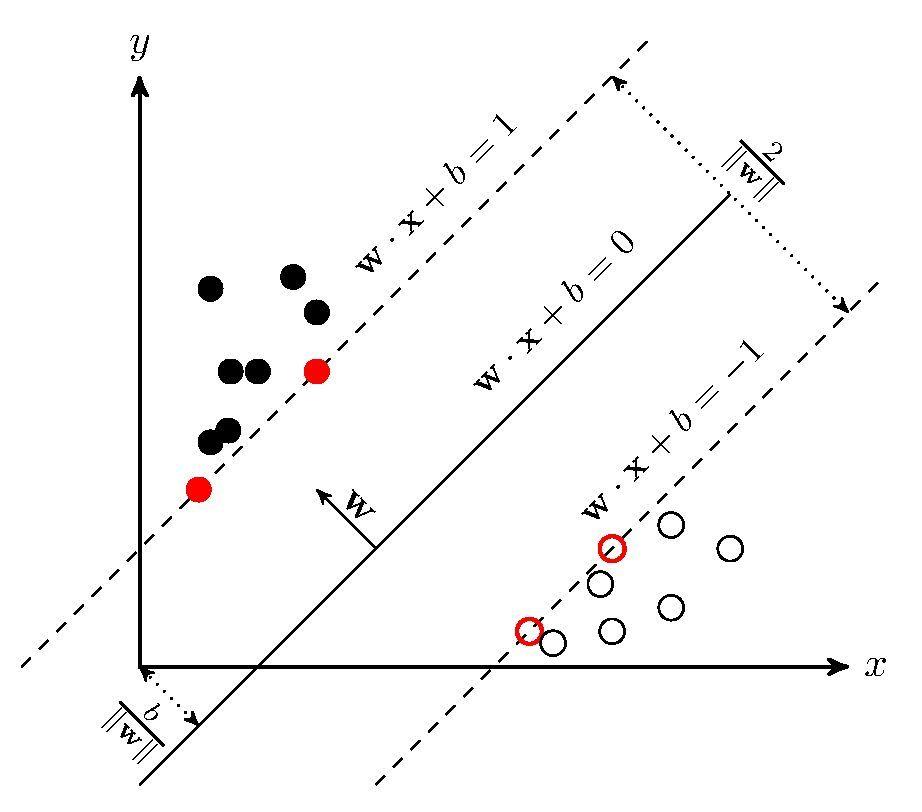
2. 函数间隔（Functional Margin）与几何间隔（Geometrical Margin）

函数间隔

当在一个超平面$w^{T}x+b=0$确定的情况下，我们可以看到$|w^T{x}_i+b|$能够反映点$x_i$到超平面的远近（但不是实际的欧几里得距离），通过观察$w^T{x}_i+b$和类标记$y_i$符号是否一致，可以判断分类结果是否正确。因此，同时考虑$w^T{x}_i+b$和$y_i$，即$y_i(w^T{x}_i+b)$能到的一种对于分类结果正确与否的度量（可信度）。

所以，我们定义间隔函数为：
$$\widehat{{\gamma }_i}=y_i(w^T{x}_i$$

支持向量机（SVM：support vector machine）

支持向量机(support vector machines, SVM)

机器学习之支持向量机（Support Vector Machine）（更新中...）

浅谈支持向量机（Support Vector Machine）

分类问题第二弹来袭：支持向量机（Support Vector Machine）