当分布 非正态分布时,能否使用Pearson Correlation?
Posted UQI-LIUWJ
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了当分布 非正态分布时,能否使用Pearson Correlation?相关的知识,希望对你有一定的参考价值。
主要内容来自论文:Testing the Significance of a Correlation With Nonnormal Data: Comparison of Pearson, Spearman, Transformation, and Resampling Approaches
1 先说结论
- Pearson 的 r 在 I 类错误率方面对非正态分布相对稳健,除了特别小的样本量或特别是非正态分布形状。
- 然而,其他方法具有更强大的 I 类错误控制。
- Spearman“精确”测试
- RIN 变换+Pearson
- 置换测试
- 单变量bootstrap测试
- 在所有场景中都保持了预期的 I 类错误率。
- 对于小样本(通常 n≤10),置换检验通常提供一种稳健的替代方案,其功效与 Pearson t 检验相同或更强大
- 对于较大的样本量(通常n≥ 20),RIN变换+Pearson 方法的功效优势变得明显
- 对于 I 类错误率和power,非正态性的类型很重要。
- 当一个或多个分布具有高峰态形状(例如卡方或长尾分布)时,非正态性对于 Pearson t 检验最成问题
- 这种模式不能通过方差来解释,因为实验中总体方差对于所有分布形状都是一样的
- 这些卡方分布和长尾分布特别容易出现 I 型错误膨胀。
- 在我们的模拟中,具有高度峰态分布的 Pearson t 检验不仅导致 I 类错误膨胀,而且还导致相对较低的power当
- 此时,RIN变换+Pearson 方法相对于 Pearson t 检验的功率优势尤其明显。
- 当一个或多个分布具有高峰态形状(例如卡方或长尾分布)时,非正态性对于 Pearson t 检验最成问题
(power:power of test,数值上等于1-type 2 error)
1.1 Spearman rank-order correlation的结论
- Spearman correlation是在违反“正态分布”假设时通常推荐的 Pearson 相关性替代方案。
- 对于小样本 (n=10) 的 Spearman correlation,“精确”检验比 t 检验更好地保持 I 类错误率
- 对于大样本,它们产生几乎相同的结果。
- 相对于 Pearson t 检验,Spearman correlation有时会产生显着的power改进,尤其是在样本量较大的情况下。
- 然而,即便如此,RIN变换+Pearson 方法的power仍然更高。
2 当时教科书的一些推荐
- 有一些教科书认为Pearson correlation非常稳健,可以忍受类似于“正态分布”这样的假设的丢失
- 有一些教科书则认为使用Pearson correlation必须要满足二元正态分布
- 尽管对于Pearson correlation 的稳健性有不一样的说法,但是对于Pearson correlation的替代者,教科书中的说法还是较为相似的
- 最常见的是使用Spearman rank-order correlation
- 第二常见的是normalize 非正态分布的样本,使其变得正态分布,然后使用Pearson correlation进行分析处理
- resampling的方法也有,但是不常见
3 几种方法的介绍
3.1 Pearson correlation
- 早期的模拟研究表明,在检验 ρ=0 的假设时,Pearson r 的抽样分布对非正态性的影响不敏感
- 他们的结果表明,Pearson 的 r 对非正态性、非等区间测量以及非正态性和非等区间测量的组合具有稳健性。
- 后续研究观测了非常不正态的分布,以及各种混合正态分布
- ——>大部分情况下,Pearson分布还是比较稳健的,除非样本的数量特别少
文献表明,极端非正态分布有时会提高 Pearson 相关系数检验的 I 类错误率,增加样本量并不一定能缓解这个问题。 因此,对于非正态数据,Pearson 方法的替代方案可能是合理的。
3.2 几种测试介绍
| test名称 | test介绍 |
| Pearson —t test | 传统的Pearson product-moment |
| Pearson —z test | 对pearson结果进行变换
|
| Spearman —t test | 传统的Spearman rank-order correlation |
| Spearman —‘exact’ test |
|
| Box-Cox 变换+Pearson(先变换再Pearson) | Box-Cox变换:
|
| Yeo-Johnson变换+Pearson | Box-COx的一个限制条件是它需要数据是正的。 ——>为了解决之,Yeo-Johnson出现了
Box-Cox 和 Yeo-Johnson 方法特别适用于偏斜的数据,但不太适用于对称数据。 |
| Arcsine变换+Pearson | 反正弦变换可以有效地将均匀分布数据转换为正态分布数据
这里a,b是X中的最小和最大值,k是为了分母非空,k=0.01 |
| RIN 变换+Pearson |
|
| 置换测试 |
|
| 单变量bootstrap测试 |
|
| 双变量Bootsrap测试 BCa 测试 | 略 |
4 实验部分
4.1 使用的分布类型
使用了6种分布:normal,Weibull,Chi-squared,uniform,bimodal,long-tailed
——》所有分布均值皆为0,标准差皆为1

- (一开始我以为长尾分布和normal画反了,后来我查了下长尾分布的特点,发现是我搞错了)
- 长尾分布 极少数个体(横轴)对应极高的值(纵轴),而拥有极低值的个体,数量却占总体的绝大多数。
4.2 其他参数
样本数量:六个样本大小为n=5,10,20,40,80,160
ρ=0被用于0 关联度的Ho;0.1用作小effect size;0.5用作大effect size
4.3 实验结果
4.3.1 1类误差
表 2 显示了 I 类错误率,即当总体中 X 和 Y 之间没有关联时(ρ=0)错误拒绝原假设的概率。 表中的粗体值显示 I 类错误超过 0.060 的情况。 【也就是误差很大的时候】

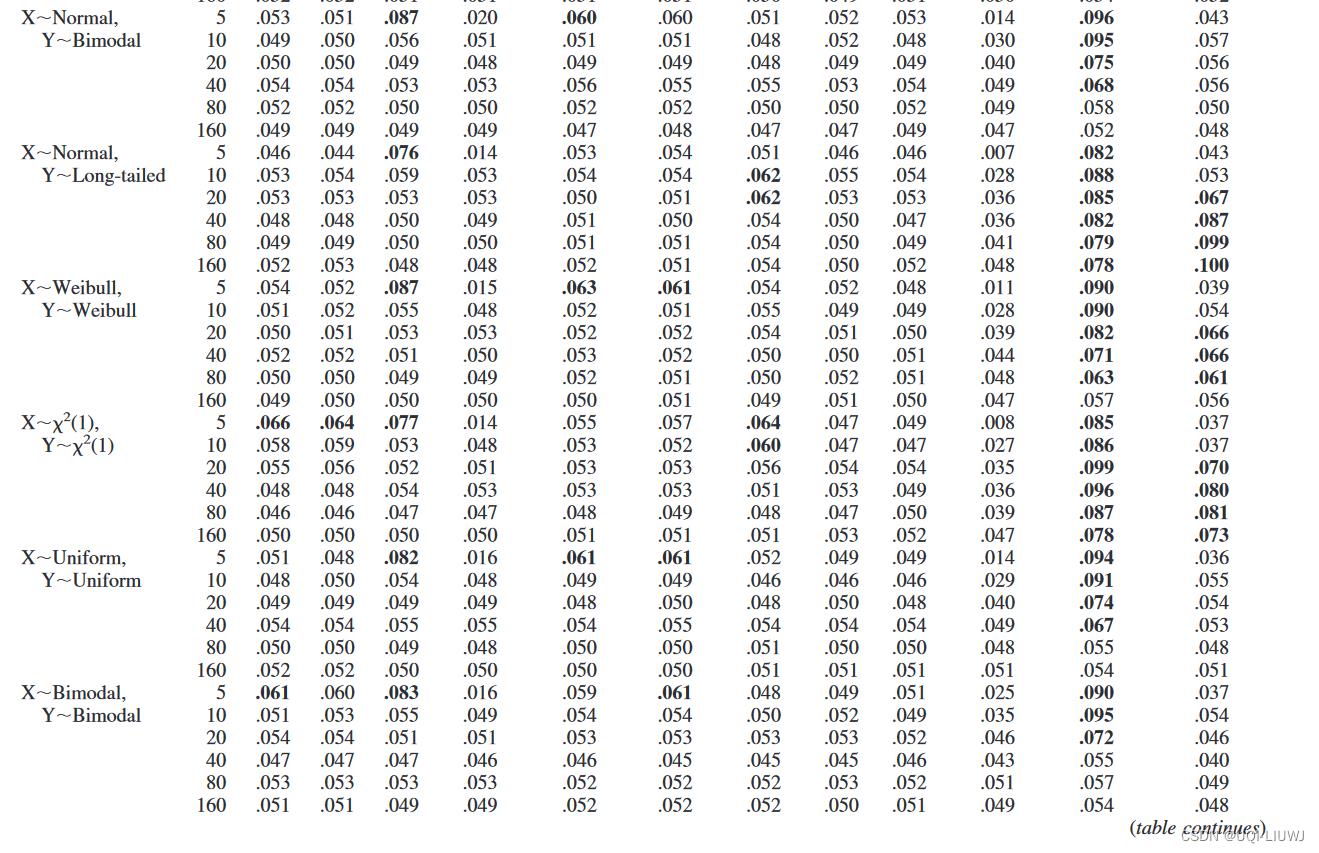
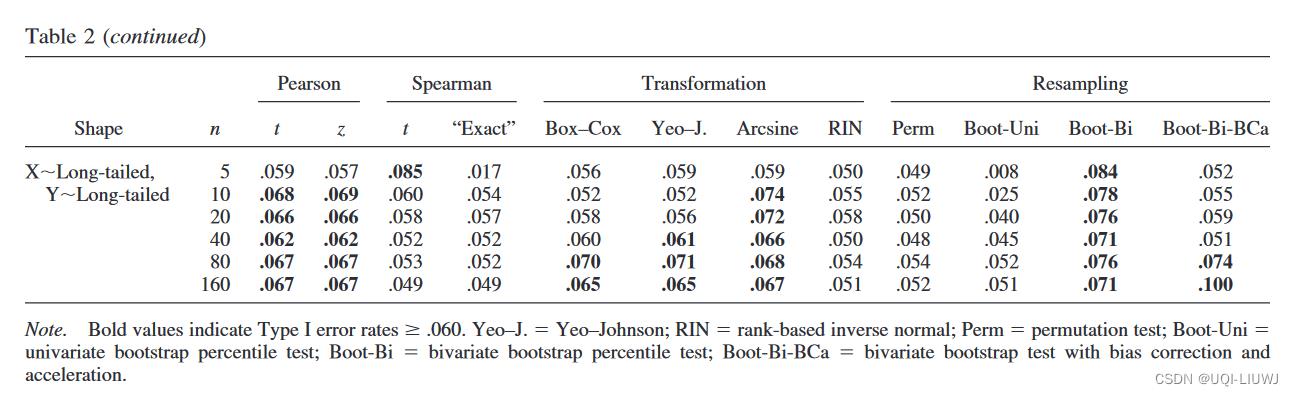
可以得到的几个结论是:
- 两种Pearson的方法大部分情况下都是很稳定的,只有当X,Y都有极端outlier时,Type I error才会有一些上升
- 当n≥20的时候,两种Spearman correlation都是稳定的
- 对于小的n,t验证的Spearman correlation会有较大的type 1 error;‘exact’ spearman则不会
- 在所有先变换再Pearson的方法中,只有RIN是一直稳定的
- 其他的方法在极端非正态分布/n很小时,Type 1 error就会提升
- 在所有resample方法中,只有permutation和单变量bootstrap是稳定的
——>只有四种方法会一直将type 1 error保持在很低的值
- Spearman“精确”测试
- RIN 变换+Pearson
- 置换测试
- 单变量bootstrap测试
4.3.2 power of test

- 至少有一个变量的分布非正态分布后,几种上一小节稳定的方法之间还是有差距的
- 在样本数量大于20时,RIN有最好/近似最好的statistical power
以上是关于当分布 非正态分布时,能否使用Pearson Correlation?的主要内容,如果未能解决你的问题,请参考以下文章



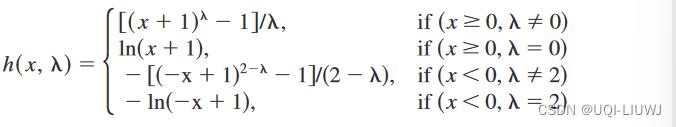
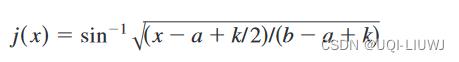
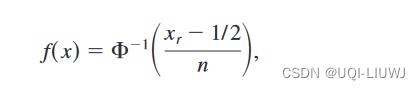
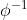 是逆正态累积分布函数
是逆正态累积分布函数