多维数据结构与运算

Posted 2022-11-19 山川绿水

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了多维数据结构与运算相关的知识，希望对你有一定的参考价值。

数据科学技术与应用——第2章多维数据结构与运算

2.1 多维数据对象

例题如下

例题[2-1] 创建两个一维数组风别保存学生姓名和考试科目，访问数组元素。学业水平考试涉及多门课程和多名学生，虽然课程名称、姓名的数据类型都是字符串，但是对应的现实概念却不同，需存放两个一位数组中。

>>> import numpy as np
>>> names = np.array(['王薇','肖良英','方绮雯','刘旭阳','钱易铭'])
>>> names
array(['王薇', '肖良英', '方绮雯', '刘旭阳', '钱易铭'], dtype='<U3')
>>> subjects = np.array(['Math','English','Python','Chinese','Art','Database','Physics'])
>>> subjects
array(['Math', 'English', 'Python', 'Chinese', 'Art', 'Database',
       'Physics'], dtype='<U8')
>>>

[例题2-2] 创建二维数组scores,记录names中每名学生对应subjects各门课程的考试成绩。

>>> scores = np.array([[70,85,77,90,82,84,89],[60,64,80,75,80,92,90],[90,93,88,87,86,90,91],[80,82,91,88,83,86,80],[88,72,78,90,91,73,80]])
>>> scores
array([[70, 85, 77, 90, 82, 84, 89],
       [60, 64, 80, 75, 80, 92, 90],
       [90, 93, 88, 87, 86, 90, 91],
       [80, 82, 91, 88, 83, 86, 80],
       [88, 72, 78, 90, 91, 73, 80]])
>>>

思考练习

1.一维数组访问

（1）在subjects数组中选择显示序号为：1、2、4科目的名称，使用倒序索引选择并显示names数组的“方绮雯”。

>>> subjects[[1,2,4]]
array(['English', 'Python', 'Art'], dtype='<U8')
>>> names[-3]
'方绮雯'
>>>

（2）选择并显示names数组从2到最后的数组元素，选择并显示subjects数组正序2~4的数组元素。

>>> names[2:]
array(['方绮雯', '刘旭阳', '钱易铭'], dtype='<U3')
>>> subjects[2:5]
array(['Python', 'Chinese', 'Art'], dtype='<U8')
>>>

（3）使用布尔条件选择并显示subjects数组中English和physics的科目名称。

>>> subjects[(subjects == 'English')|(subjects == 'Physics')]
array(['English', 'Physics'], dtype='<U8')
>>>

2.二维数组访问

(1)选择并显示scores数组的1行，4行。

>>> scores
array([[70, 85, 77, 90, 82, 84, 89],
       [60, 64, 80, 75, 80, 92, 90],
       [90, 93, 88, 87, 86, 90, 91],
       [80, 82, 91, 88, 83, 86, 80],
       [88, 72, 78, 90, 91, 73, 80]])
>>> scores[[1,4]]
array([[60, 64, 80, 75, 80, 92, 90],
       [88, 72, 78, 90, 91, 73, 80]])
>>>

(2)选择并显示scores数组中行序为2，4学生的Math和Python成绩。

>>> subjects
array(['Math', 'English', 'Python', 'Chinese', 'Art', 'Database',
       'Physics'], dtype='<U8')
>>> scores
array([[70, 85, 77, 90, 82, 84, 89],
       [60, 64, 80, 75, 80, 92, 90],
       [90, 93, 88, 87, 86, 90, 91],
       [80, 82, 91, 88, 83, 86, 80],
       [88, 72, 78, 90, 91, 73, 80]])
>>> scores[[1,3]]
array([[60, 64, 80, 75, 80, 92, 90],
       [80, 82, 91, 88, 83, 86, 80]])
>>> scores[[1,3]][:,(subjects=='Math')|(subjects== 'Python')]
array([[60, 80],
       [80, 91]])
>>>

(3)选择并显示scores数组中所有学生的Math和Art成绩。

>>> subjects
array(['Math', 'English', 'Python', 'Chinese', 'Art', 'Database',
       'Physics'], dtype='<U8')
>>> scores
array([[70, 85, 77, 90, 82, 84, 89],
       [60, 64, 80, 75, 80, 92, 90],
       [90, 93, 88, 87, 86, 90, 91],
       [80, 82, 91, 88, 83, 86, 80],
       [88, 72, 78, 90, 91, 73, 80]])
>>> scores[:,(subjects=='Math')|(subjects== 'Art')]
array([[70, 82],
       [60, 80],
       [90, 86],
       [80, 83],
       [88, 91]])
>>>

(4)选择并显示scores数组中“王薇”和“刘旭阳”的English和Art成绩。

>>> names
array(['王薇', '肖良英', '方绮雯', '刘旭阳', '钱易铭'], dtype='<U3')
>>> scores
array([[70, 85, 77, 90, 82, 84, 89],
       [60, 64, 80, 75, 80, 92, 90],
       [90, 93, 88, 87, 86, 90, 91],
       [80, 82, 91, 88, 83, 86, 80],
       [88, 72, 78, 90, 91, 73, 80]])
>>> subjects
array(['Math', 'English', 'Python', 'Chinese', 'Art', 'Database',
       'Physics'], dtype='<U8')
>>> scores[(names == 'English')|(names == 'Art')]
array([], shape=(0, 7), dtype=int32)
>>> scores[(names == '王薇')|(names == '刘旭阳')][:,(subjects == 'English')|(subjects == 'Art')]
array([[85, 82],
       [82, 83]])
>>>

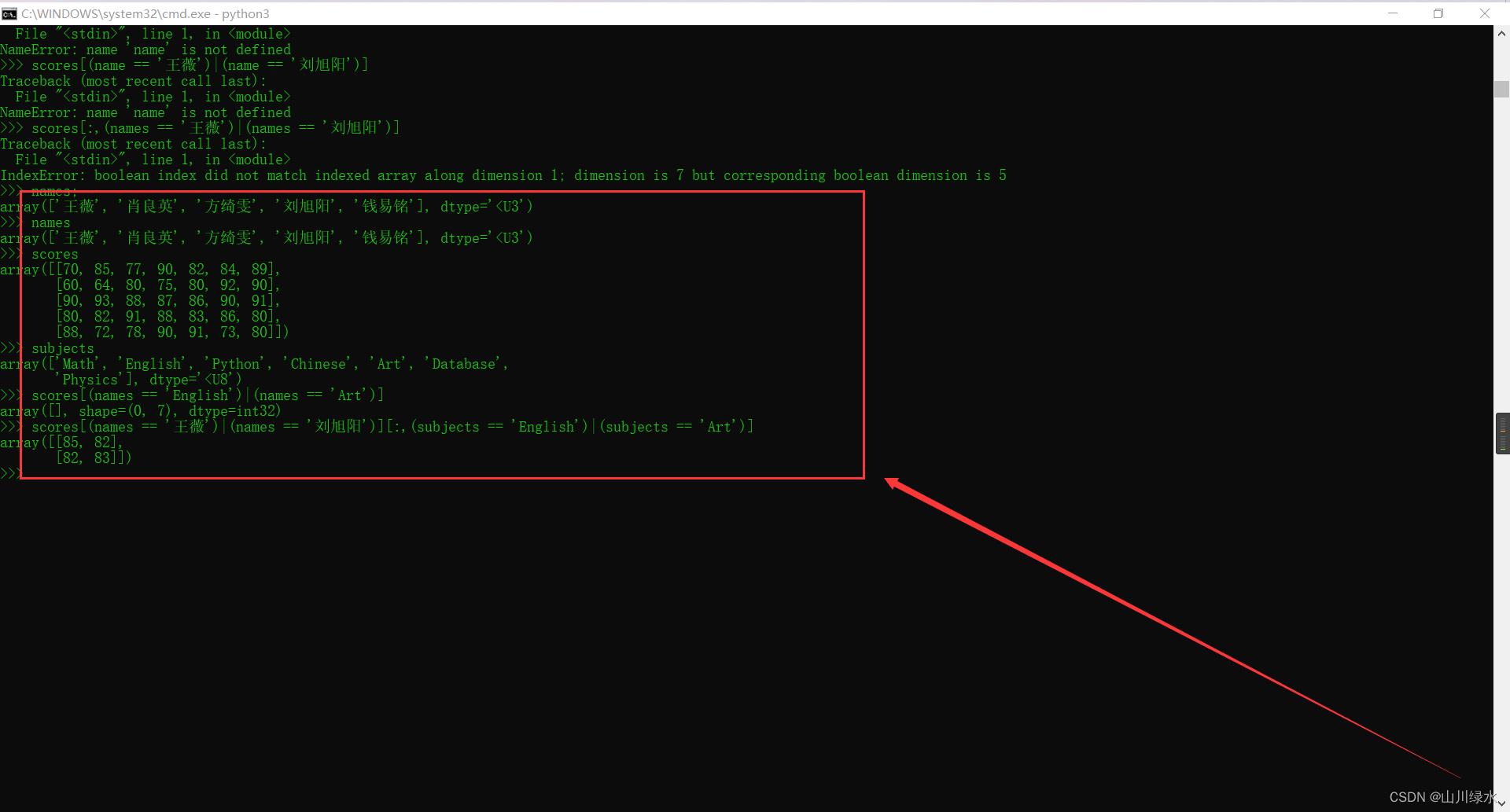
3.生成有整数10~19组成的2 x 5的二维数组。

>>> np.arange(10,20).reshape(2,5)
array([[10, 11, 12, 13, 14],
       [15, 16, 17, 18, 19]])
>>>

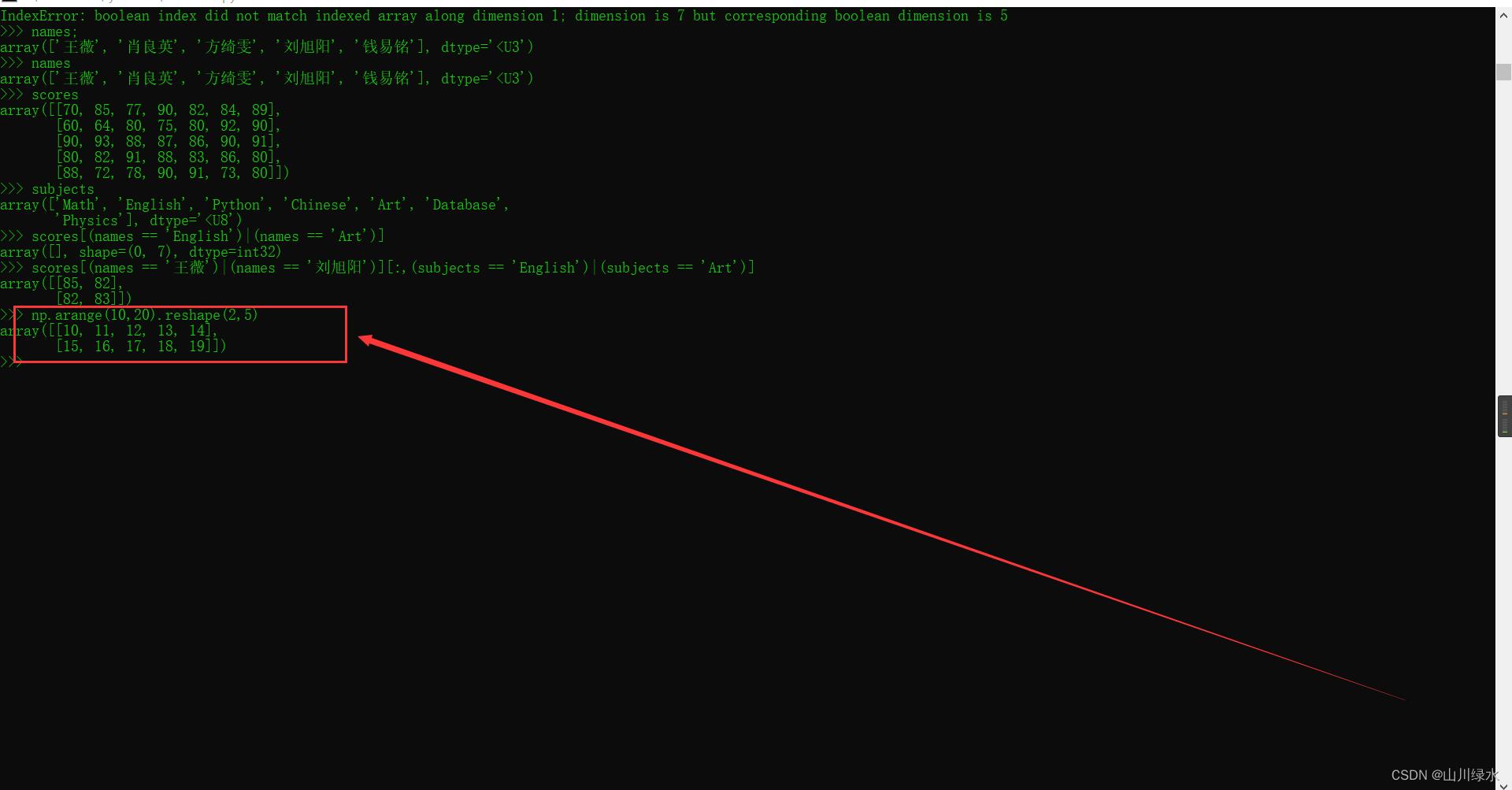
2.2 多维数组运算

例题如下

例题[2-3] 为所有学生的所有课程成绩增加5分

>>> scores
array([[70, 85, 77, 90, 82, 84, 89],
       [60, 64, 80, 75, 80, 92, 90],
       [90, 93, 88, 87, 86, 90, 91],
       [80, 82, 91, 88, 83, 86, 80],
       [88, 72, 78, 90, 91, 73, 80]])
>>> scores + 5
array([[75, 90, 82, 95, 87, 89, 94],
       [65, 69, 85, 80, 85, 97, 95],
       [95, 98, 93, 92, 91, 95, 96],
       [85, 87, 96, 93, 88, 91, 85],
       [93, 77, 83, 95, 96, 78, 85]])
>>>

Python内部实现数组与标量相加时，使用“广播机制”先将标量5转换成元素值为5的5 x 7二维数组，再将scores和新生成的数组按位相加，等价于以下代码。

>>> scores
array([[70, 85, 77, 90, 82, 84, 89],
       [60, 64, 80, 75, 80, 92, 90],
       [90, 93, 88, 87, 86, 90, 91],
       [80, 82, 91, 88, 83, 86, 80],
       [88, 72, 78, 90, 91, 73, 80]])
>>> a = np.ones((5,7))
>>> a
array([[1., 1., 1., 1., 1., 1., 1.],
       [1., 1., 1., 1., 1., 1., 1.],
       [1., 1., 1., 1., 1., 1., 1.],
       [1., 1., 1., 1., 1., 1., 1.],
       [1., 1., 1., 1., 1., 1., 1.]])
>>> a = np.ones((5,7))*5
>>> a
array([[5., 5., 5., 5., 5., 5., 5.],
       [5., 5., 5., 5., 5., 5., 5.],
       [5., 5., 5., 5., 5., 5., 5.],
       [5., 5., 5., 5., 5., 5., 5.],
       [5., 5., 5., 5., 5., 5., 5.]])
>>> scores + a
array([[75., 90., 82., 95., 87., 89., 94.],
       [65., 69., 85., 80., 85., 97., 95.],
       [95., 98., 93., 92., 91., 95., 96.],
       [85., 87., 96., 93., 88., 91., 85.],
       [93., 77., 83., 95., 96., 78., 85.]])
>>>

例题[2-4] 首先创建一维数组存放不同科目增加分数，然后将其和scores相加。

>>> bonus = np.array([3,4,5,3,6,7,2])
>>> scores + bonus
array([[73, 89, 82, 93, 88, 91, 91],
       [63, 68, 85, 78, 86, 99, 92],
       [93, 97, 93, 90, 92, 97, 93],
       [83, 86, 96, 91, 89, 93, 82],
       [91, 76, 83, 93, 97, 80, 82]])
>>>

例题[2-5]将学生的考试成绩转换为整数形式的十分制分数

>>> np.floor(scores/10)
array([[7., 8., 7., 9., 8., 8., 8.],
       [6., 6., 8., 7., 8., 9., 9.],
       [9., 9., 8., 8., 8., 9., 9.],
       [8., 8., 9., 8., 8., 8., 8.],
       [8., 7., 7., 9., 9., 7., 8.]])
>>>

例题[2-6] 使用subtract()给每个学生的分数减去3分

>>> np.subtract(scores,3)
array([[67, 82, 74, 87, 79, 81, 86],
       [57, 61, 77, 72, 77, 89, 87],
       [87, 90, 85, 84, 83, 87, 88],
       [77, 79, 88, 85, 80, 83, 77],
       [85, 69, 75, 87, 88, 70, 77]])
>>>

例题[2-7] 按照分析目标使用聚合函数进行统计。

(1)统计不同科目的成绩总分。
当axis=0时，按列求和；当axis=1时，按行求和

>>> scores
array([[70, 85, 77, 90, 82, 84, 89],
       [60, 64, 80, 75, 80, 92, 90],
       [90, 93, 88, 87, 86, 90, 91],
       [80, 82, 91, 88, 83, 86, 80],
       [88, 72, 78, 90, 91, 73, 80]])
>>> scores.sum(axis = 0)
array([388, 396, 414, 430, 422, 425, 430])
>>> scores.sum(axis = 1)
array([577, 541, 625, 590, 572])
>>>

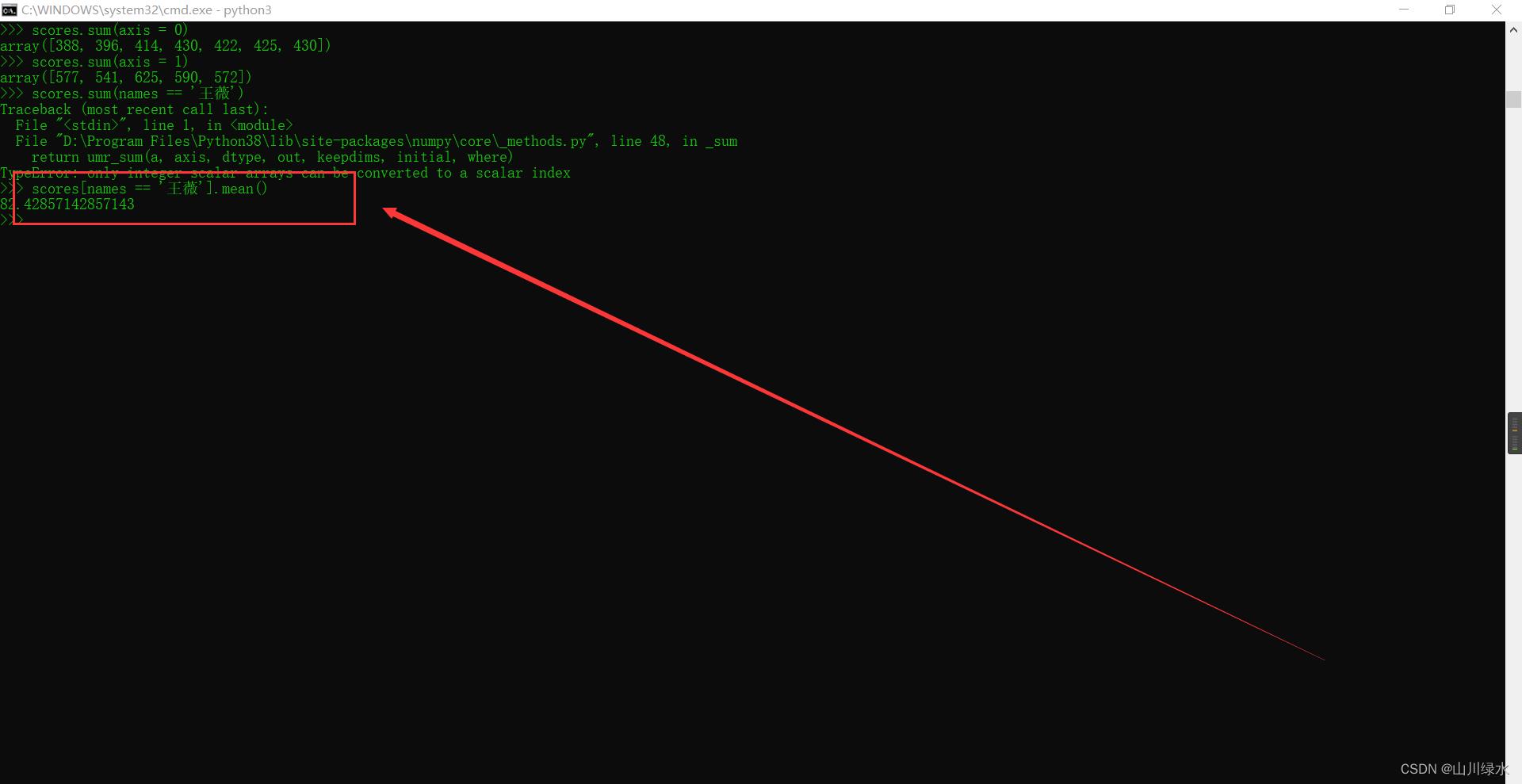
（2）求王薇所有课程成绩的平均分

>>> scores[names == '王薇'].mean()
82.42857142857143
>>>

(3)查询英语考试成绩最高的学生姓名。

>>> names[scores[:,subjects == 'English'].argmax()]
'方绮雯'
>>>

例题[2-8] 生成由10个随机整数组成的一维数组，整数的取值范围为0~5

>>> np.random.randint(0,6,10)
array([2, 0, 0, 1, 3, 4, 4, 3, 5, 4])
>>>

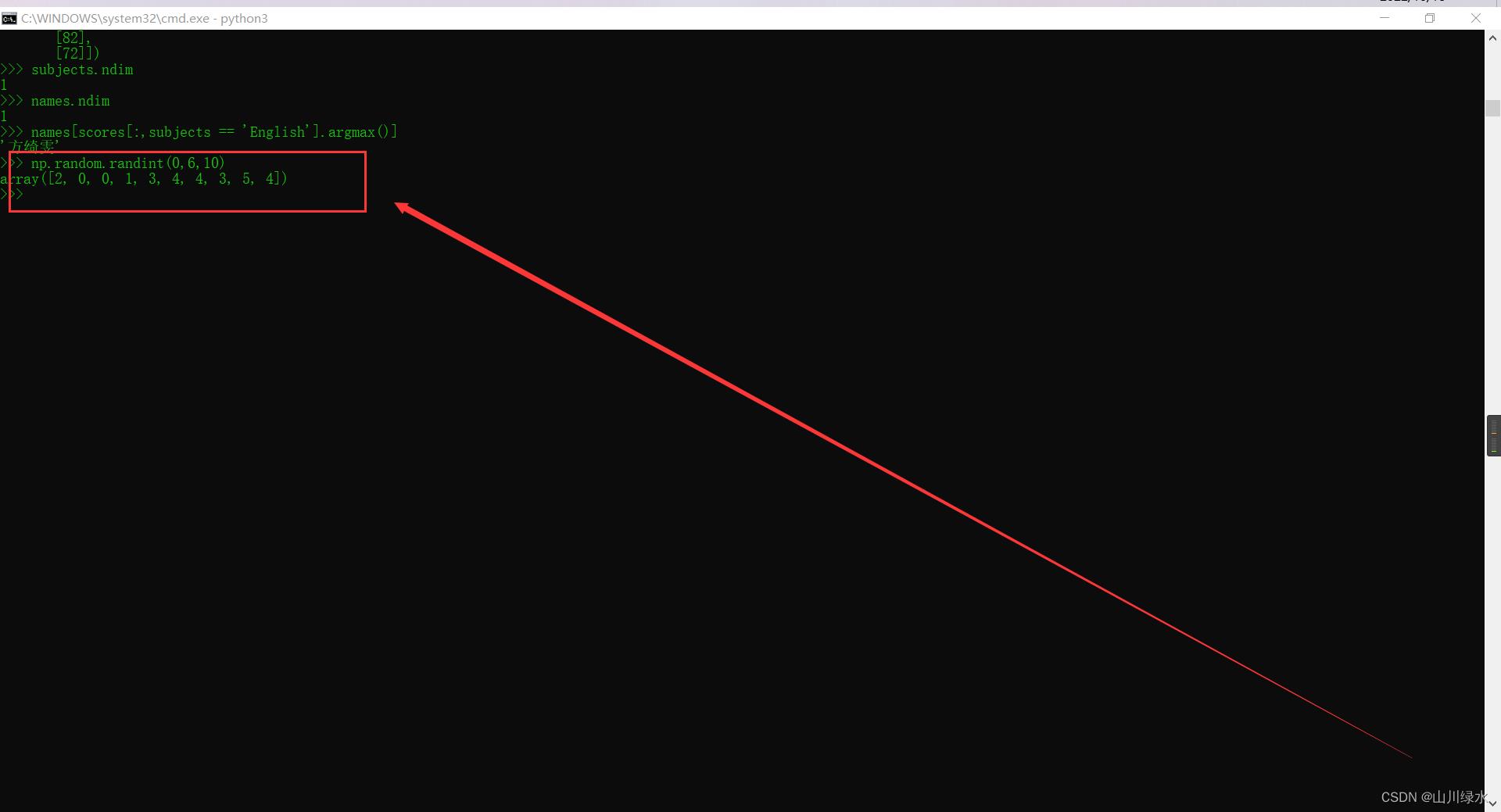
randint(start,end,size)生成元素值从start到end-1范围内的整数数组，数组的大小由参数size对应的元组给出。数组的元素值随机生成，start到end-1范围内各整数出现的概率相等。

生成5x6的二维随机整数，随机数的数值是0或1.

>>> np.random.randint(0,2,size=(5,6))
array([[0, 1, 0, 0, 1, 1],
       [1, 0, 1, 0, 1, 1],
       [1, 1, 0, 1, 0, 0],
       [0, 0, 0, 0, 0, 0],
       [0, 0, 0, 0, 0, 0]])
>>>

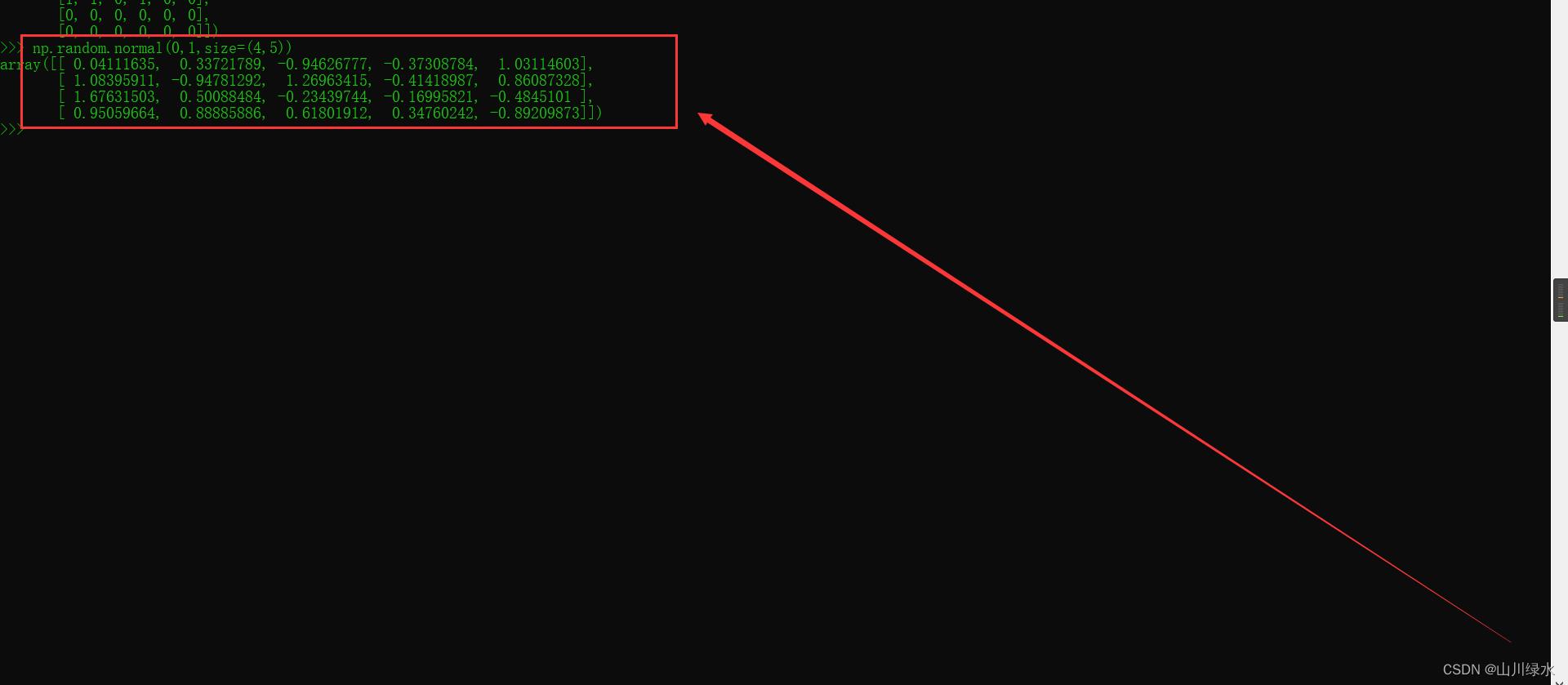
例题[2-9] 生成均值为0、方差为1服从正态分布的4 x 5二维数组。

>>> np.random.normal(0,1,size=(4,5))
array([[ 0.04111635,  0.33721789, -0.94626777, -0.37308784,  1.03114603],
       [ 1.08395911, -0.94781292,  1.26963415, -0.41418987,  0.86087328],
       [ 1.67631503,  0.50088484, -0.23439744, -0.16995821, -0.4845101 ],
       [ 0.95059664,  0.88885886,  0.61801912,  0.34760242, -0.89209873]])
>>>

思考与练习

1.将scores数组中所有学生的英语成绩减去3分并显示

>>> scores
array([[70, 85, 77, 90, 82, 84, 89],
       [60, 64, 80, 75, 80, 92, 90],
       [90, 93, 88, 87, 86, 90, 91],
       [80, 82, 91, 88, 83, 86, 80],
       [88, 72, 78, 90, 91, 73, 80]])
>>> subjects
array(['Math', 'English', 'Python', 'Chinese', 'Art', 'Database',
       'Physics'], dtype='<U8')
>>> scores[:,subjects='English']
  File "<stdin>", line 1
    scores[:,subjects='English']
                     ^
SyntaxError: invalid syntax
>>> scores[:,subjects == 'English']
array([[85],
       [64],
       [93],
       [82],
       [72]])
>>> scores[:,subjects == 'English'] - 3
array([[82],
       [61],
       [90],
       [79],
       [69]])
>>>

2.统计scores数组中每名学生所有科目的平均分并显示

>>> scores.mean(axis = 1)
array([82.42857143, 77.28571429, 89.28571429, 84.28571429, 81.71428571])
>>> x = scores.mean(axis = 1)     #按行求平均数
>>>> print(x[0])
82.42857142857143
>>> print("1",x[0])
1 82.42857142857143
>>> print(names[0],x[0])
王薇 82.42857142857143
>>> print(names[0],"平均分",x[0])
王薇 平均分 82.42857142857143
>>> names
array(['王薇', '肖良英', '方绮雯', '刘旭阳', '钱易铭'], dtype='<U3')
>>> for i in range(0,5):
... print(i)
  File "<stdin>", line 2
    print(i)
    ^
IndentationError: expected an indented block
>>> for i in range(0,5):
...     print(i)
...
0
1
2
3
4
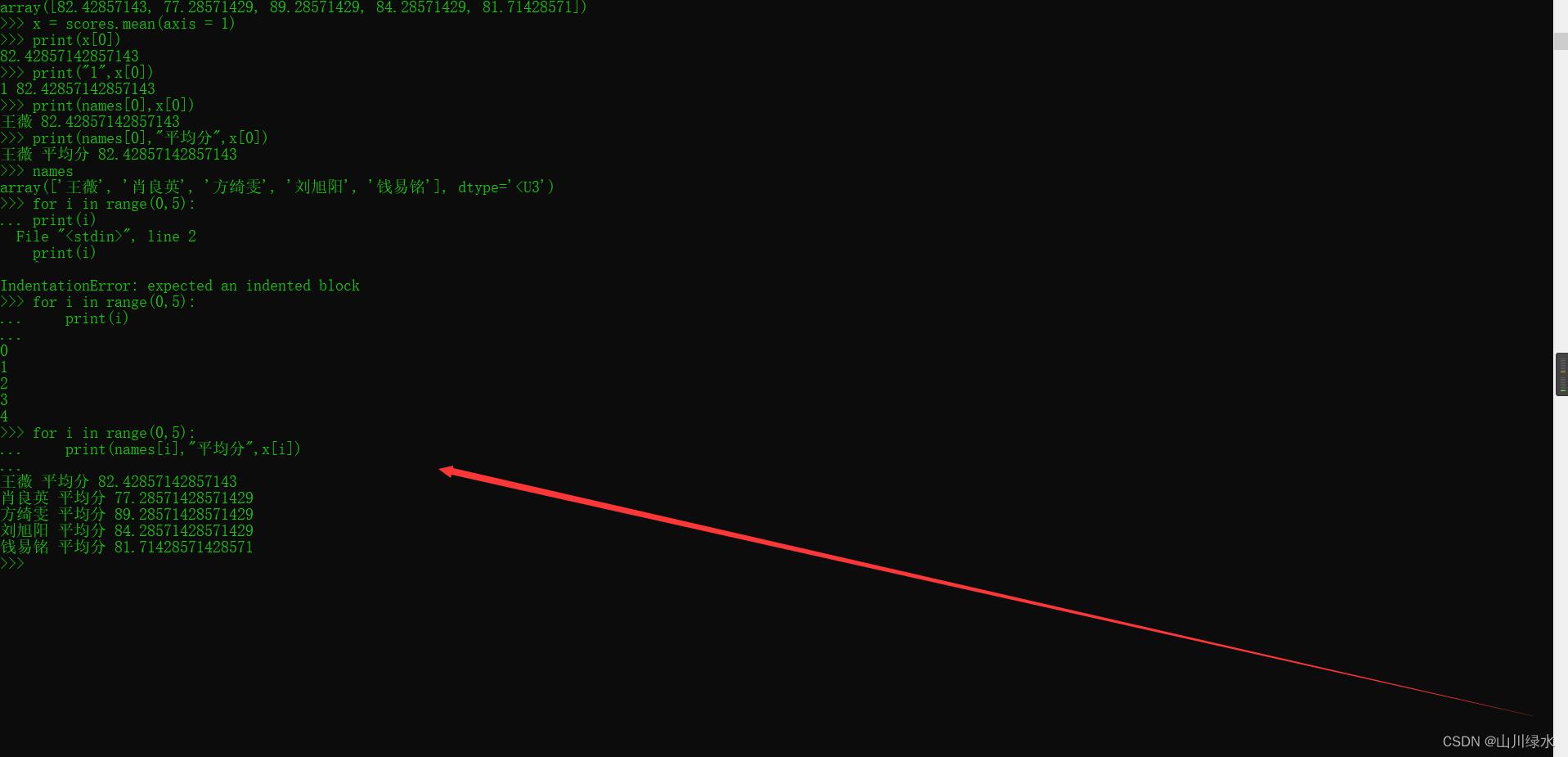
>>> for i in range(0,5):
...     print(names[i],"平均分",x[i])
...
王薇 平均分 82.42857142857143
肖良英 平均分 77.28571428571429
方绮雯 平均分 89.28571428571429
刘旭阳 平均分 84.28571428571429
钱易铭 平均分 81.71428571428571
>>>

3.使用随机函数生成[-1,1]之间服从均匀分布的3 x 4的二维数组，并计算所有元素的和

>>> temp = np.random.randint(-1,2,size=(3,4))
>>> temp
array([[ 0, -1, -1, -1],
       [-1, -1,  1, -1],
       [ 0,  0, -1,  0]])
>>> temp.sum()
-6
>>>

2.3案例：随机游走轨迹模拟

1.模拟生成每步移动方向

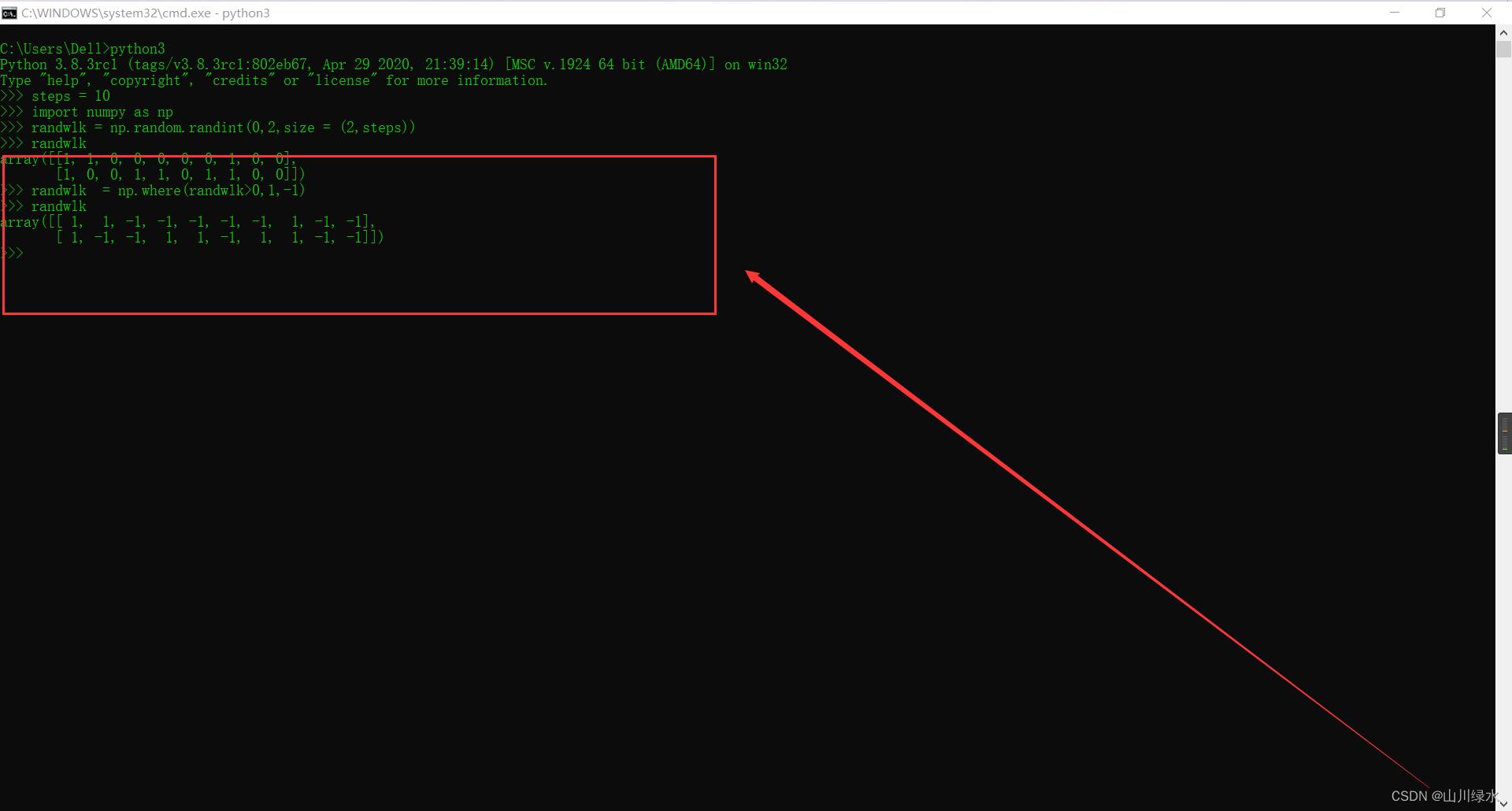
假设某次随机游走了10步，用randint()随机生成每步移动的方向，可以使用一个2 x 10的二维数组记录结果。

>>> steps = 10
>>> import numpy as np
>>> randwlk = np.random.randint(0,2,size = (2,steps))
>>> randwlk
array([[1, 1, 0, 0, 0, 0, 0, 1, 0, 0],
       [1, 0, 0, 1, 1, 0, 1, 1, 0, 0]])
>>>

Numpy提供where(condition[,x,y])实现数组元素的条件赋值，参数condition是条件表达式，如果condition结果为True，返回x，否则返回y。x、y可以是数组，也可以是标量。

>>> randwlk  = np.where(randwlk>0,1,-1)
>>> randwlk
array([[ 1,  1, -1, -1, -1, -1, -1,  1, -1, -1],
       [ 1, -1, -1,  1,  1, -1,  1,  1, -1, -1]])
>>>

2.计算每步移动后的位置

rndwlk记录了物体每步沿着x轴，y轴移动的方向，计算第i步所处的位置只需分别累计从第1步到第i步沿x轴、y轴移动的单位总和即可。使用ndarray对象的聚合函数cumsum()就可以实现此功能。

>>> position = randwlk.cumsum(axis = 1)
>>> position
array([[ 1,  2,  1,  0, -1, -2, -3, -2, -3, -4],
       [ 1,  0, -1,  0,  1,  0,  1,  2,  1,  0]])
>>>

3.计算每步移动后与原点的距离

利用算数运算符和通用函数，可以算出物体在每步移动后与原点的距离。若计算得到浮点数位数太长，则可以使用np.set_printoptions()设置现实的小数位数。

>>> dists = np.sqrt(position[0]**2 + position[1]**2)
>>> dists
array([1.41421356, 2.        , 1.41421356, 0.        , 1.41421356,
       2.        , 3.16227766, 2.82842712, 3.16227766, 4.        ])
>>> np.set_printoptions(precision = 4)
>>> dists
array([1.4142, 2.    , 1.4142, 0.    , 1.4142, 2.    , 3.1623, 2.8284,
       3.1623, 4.    ])
>>>

对数组dists统计物体与原点距离的最大值、最小值和平均值。

>>> dists.max()
4.0
>>> dists.min()
0.0
>>> dists.mean()
2.1395623132202237
>>>

统计物体随机游走过程中与原点的距离大于平均距离的次数

>>> (dists>dists.mean()).sum()
4
>>>

思考与练习

1.将随机游走的步数增加到100步，计算物体最终与原点的距离。

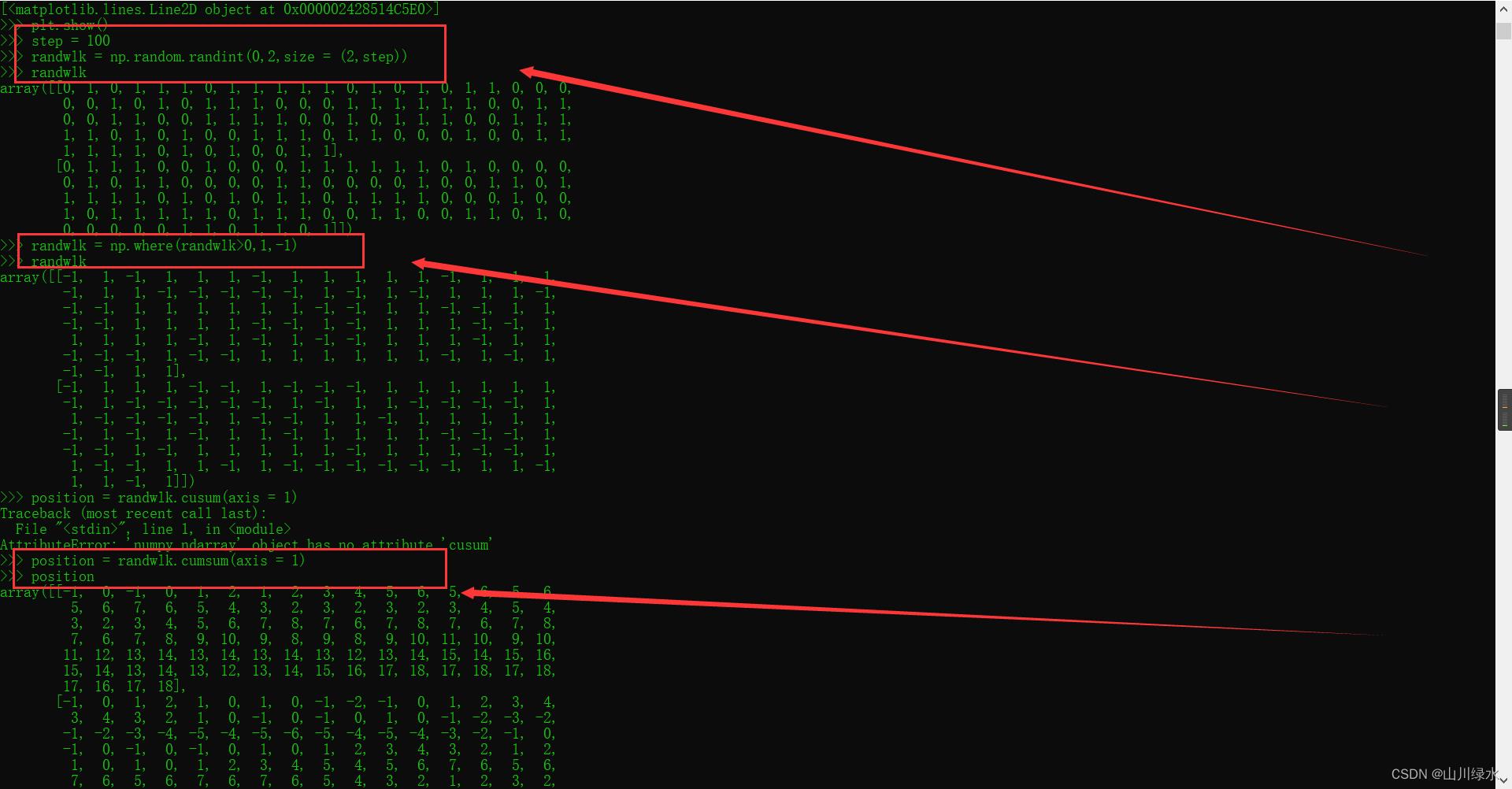
>>> step = 100
>>> randwlk = np.random.randint(0,2,size = (2,step))
>>> randwlk
array([[0, 1, 0, 1, 1, 1, 0, 1, 1, 1, 1, 1, 0, 1, 0, 1, 0, 1, 1, 0, 0, 0,
        0, 0, 1, 0, 1, 0, 1, 1, 1, 0, 0, 0, 1, 1, 1, 1, 1, 1, 0, 0, 1, 1,
        0, 0, 1, 1, 0, 0, 1, 1, 1, 1, 0, 0, 1, 0, 1, 1, 1, 0, 0, 1, 1, 1,
        1, 1, 0, 1, 0, 1, 0, 0, 1, 1, 1, 0, 1, 1, 0, 0, 0, 1, 0, 0, 1, 1,
        1, 1, 1, 1, 0, 1, 0, 1, 0, 0, 1, 1],
       [0, 1, 1, 1, 0, 0, 1, 0, 0, 0, 1, 1, 1, 1, 1, 1, 0, 1, 0, 0, 0, 0,
        0, 1, 0, 1, 1, 0, 0, 0, 0, 1, 1, 0, 0, 0, 0, 1, 0, 0, 1, 1, 0, 1,
        1, 1, 1, 1, 0, 1, 0, 1, 0, 1, 1, 0, 1, 1, 1, 1, 0, 0, 0, 1, 0, 0,
        1, 0, 1, 1, 1, 1, 1, 0, 1, 1, 1, 0, 0, 1, 1, 0, 0, 1, 1, 0, 1, 0,
        0, 0, 0, 0, 0, 1, 1, 0, 1, 1, 0, 1]])
>>> randwlk = np.where(randwlk>0,1,-1)
>>> randwlk
array([[-1,  1, -1,  1,  1,  1, -1,  1,  1,  1,  1,  1, -1,  1, -1,  1,
        -1,  1,  1, -1, -1, -1, -1, -1,  1, -1,  1, -1,  1,  1,  1, -1,
        -1, -1,  1,  1,  1,  1,  1,  1, -1, -1,  1,  1, -1, -1,  1,  1,
        -1, -1,  1,  1,  1,  1, -1, -1,  1, -1,  1,  1,  1, -1, -1,  1,
         1,  1,  1,  1, -1,  1, -1,  1, -1, -1,  1,  1,  1, -1,  1,  1,
        -1, -1, -1,  1, -1, -1,  1,  1,  1,  1,  1,  1, -1,  1, -1,  1,
        -1, -1,  1,  1],
       [-1,  1,  1,  1, -1, -1,  1, -1, -1, -1,  1,  1,  1,  1,  1,  1,
        -1,  1, -1, -1, -1, -1, -1,  1, -1,  1,  1, -1, -1, -1, -1,  1,
         1, -1, -1, -1, -1,  1, -1, -1,  1,  1, -1,  1,  1,  1,  1,  1,
        -1,  1, -1,  1, -1,  1,  1, -1,  1,  1,  1,  1, -1, -1, -1,  1,
        -1, -1,  1, -1,  1,  1,  1,  1,  1, -1,  1,  1,  1, -1, -1,  1,
         1, -1, -1,  1,  1, -1,  1, -1, -1, -1, -1, -1, -1,  1,  1, -1,
         1,  1, -1,  1]])
>>> position = randwlk.cusum(axis = 1)
Traceback (most recent call last):
  File "<stdin>", line 1, in <module>
AttributeError: 'numpy.ndarray' object has no attribute 'cusum'
>>> position = randwlk.cumsum(axis = 1)
>>> position
array([[-1,  0, -1,  0,  1,  2,  1,  2,  3,  4,  5,  6,  5,  6,  5,  6,
         5,  6,  7,  6,  5,  4,  3,  2,  3,  2,  3,  2,  3,  4,  5,  4,
         3,  2,  3,  4,  5,  6,  7,  8,  7,  6,  7,  8,  7,  6,  7,  8,
         7,  6,  7,  8,  9, 10,  9,  8,  9,  8,  9, 10, 11, 10,  9, 10,
        11, 12, 13, 14, 13, 14, 13, 14, 13, 12, 13, 14, 15, 14, 15, 16,
        15, 14, 13, 14, 13, 12, 13, 14, 15, 16, 17, 18, 17, 18, 17, 18,
        17, 16, 17, 18],
       [-1,  0,  1,  2,  1,  0,  1,  0, -1, -2, -1,  0,  1,  2,  3,  4,
         3,  4,  3,  2,  1,  0, -1,  0, -1,  0,  1,  0, -1, -2, -3, -2,
        -1, -2, -3, -4, -5, -4, -5, -6, -5, -4, -5, -4, -3, -2, -1,  0,
        -1,  0, -1,  0, -1,  0,  1,  0,  1,  2,  3,  4,  3,  2,  1,  2,
         1,  0,  1,  0,  1,  2,  3,  4,  5,  4,  5,  6,  7,  6,  5,  6,
         7,  6,  5,  6,  7,  6,  7,  6,  5,  4,  3,  2,  1,  2,  3,  2,
         3,  4,  3,  4]])
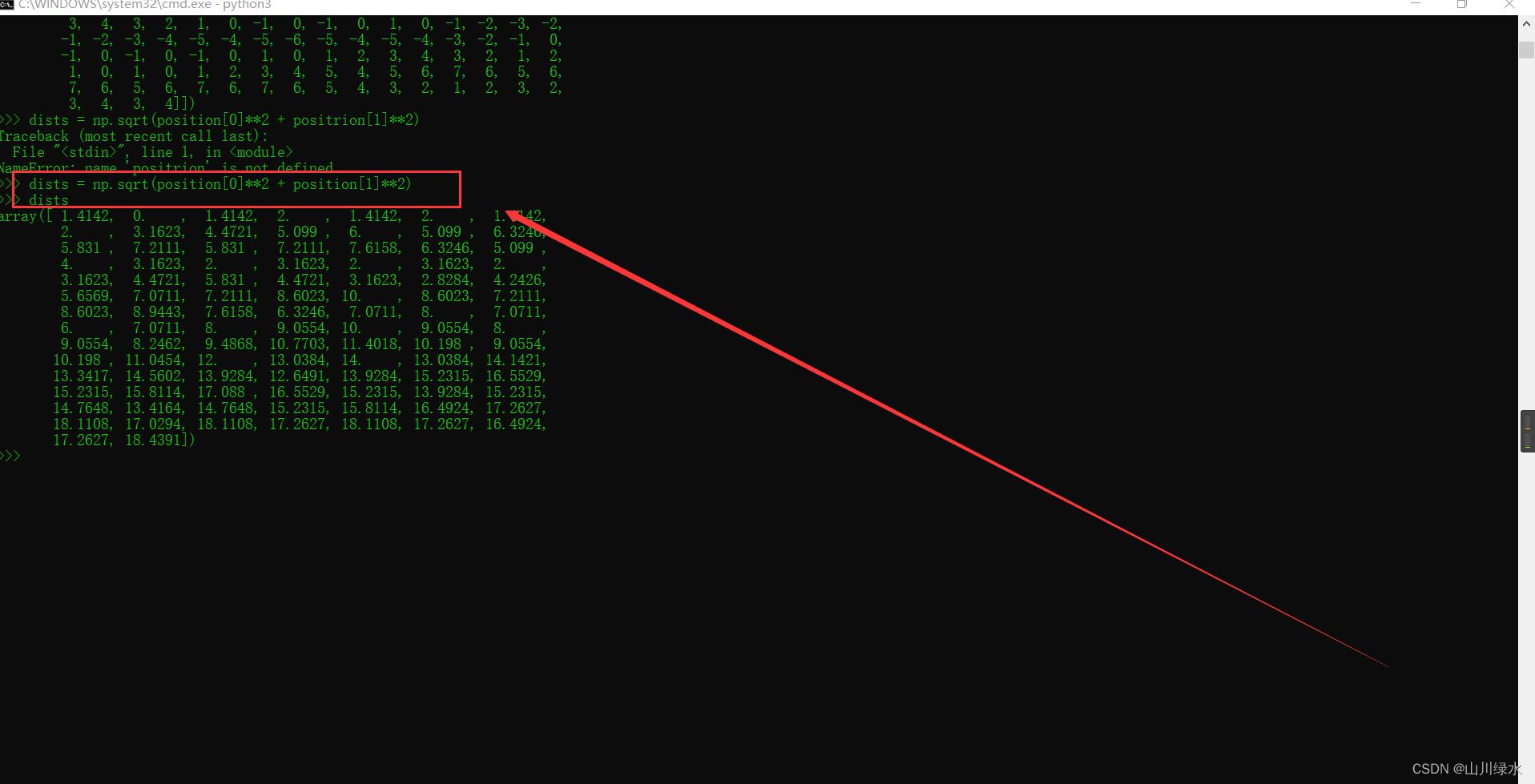
>>> dists = np.sqrt(position[0]**2 + positrion[1]**2)
Traceback (most recent call last):
  File "<stdin>", line 1, in <module>
NameError: name 'positrion' is not defined
>>> dists = np.sqrt(position[0]**2 + position[1]**2)
>>> dists
array([ 1.4142,  0.    ,  1.4142,  2.    ,  1.4142,  2.    ,  1.4142,
        2.    ,  3.1623,  4.4721,  5.099 ,  6.    ,  5.099 ,  6.3246,
        5.831 ,  7.2111,  5.831 ,  7.2111,  7.6158,  6.3246,  5.099 ,
        4.    ,  3.1623,  2.    ,  3.1623,  2.    ,  3.1623,  2.    ,
        3.1623,  4.4721,  5.831 ,  4.4721,  3.1623,  2.8284,  4.2426,
        5.6569,  7.0711,  7.2111,  8.6023, 10.    ,  8.6023,  7.2111,
        8.6023,  8.9443,  7.6158,  6.3246,  7.0711,  8.    ,  7.0711,
        6.    ,  7.0711,  8.    ,  9.0554, 10.    ,  9.0554,  8.    ,
        9.0554,  8.2462,  9.4868, 10.7703, 11.4018, 10.198 ,  9.0554,
       10.198 , 11.0454, 12.    , 13.0384, 14.    , 13.0384, 14.1421,
       13.3417, 14.5602, 13.9284, 12.6491, 13.9284, 15.2315, 16.5529,
       15.2315, 15.8114, 17.088 , 16.5529, 15.2315, 13.9284, 15.2315,
       14.7648, 13.4164, 14.7648, 15.2315, 15.8114, 16.4924, 17.2627,
       18.1108, 17.0294, 18.1108, 17.2627, 18.1108, 17.2627, 16.4924,
       17.2627, 18.4391])
>>>

综合练习题

1.大润发、沃尔玛、好德和农工商4个超市售卖苹果、梨、香蕉、橘子和芒果5种水果。使用numpy的ndarray实现以下功能。

(1)创建两个一维数组分别存储超市名称和水果名称。

>>> import numpy as np
>>> fruit = np.array(['苹果','梨','香蕉','橘子','芒果'])
>>> sup = np.array(['大润发','沃尔玛','好德','农工商'])
>>> sup
array(['大润发', '沃尔玛', '好德', '农工商'], dtype='<U3')
>>> fruit
array(['苹果', '梨', '香蕉', '橘子', '芒果'], dtype='<U2')
>>>

(2)创建4 x 5的二维数组存储不同超市的水果价格，其中价格（单位为元）由4~10范围内的随机数生成。

>>> price = np.random.randint(4,11,size = (4,5))
>>> price
array([[ 4,  7,  7,  7,  6],
       [ 4,  8,  4,  4,  4],
       [ 7,  9, 10,  7,  9],
       [ 8,  7,  5,  8,  4]])
>>>

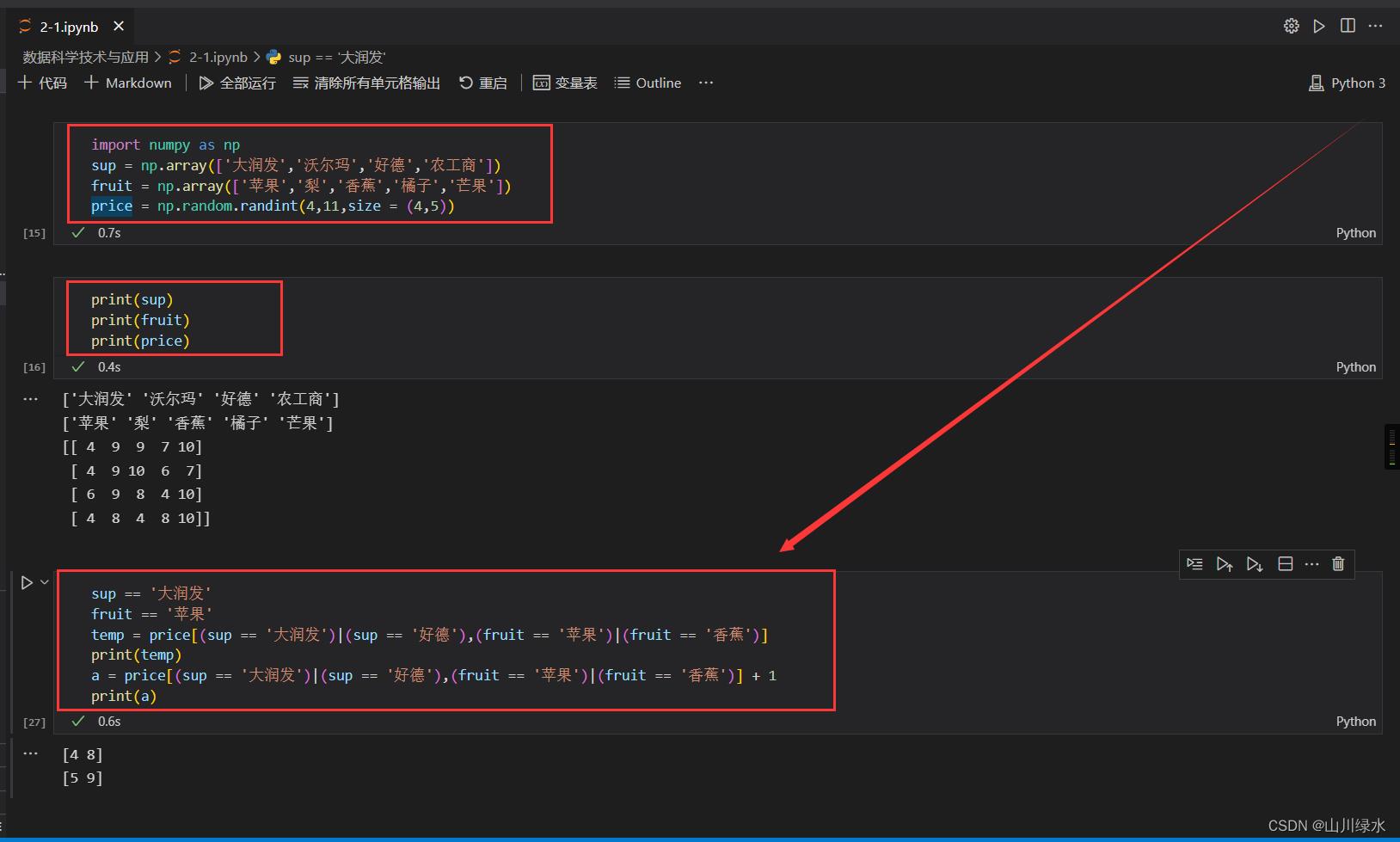
(3)选择大润发的苹果和好德的香蕉，并将价格增加1

sup == '大润发'
fruit == '苹果'
temp = price[(sup == '大润发')|(sup == '好德'),(fruit == '苹果')|(fruit == '香蕉')]
print(temp)
a = price[(sup == '大润发')|(sup == '好德'),(fruit == '苹果')|(fruit == '香蕉')] + 1
print(a)

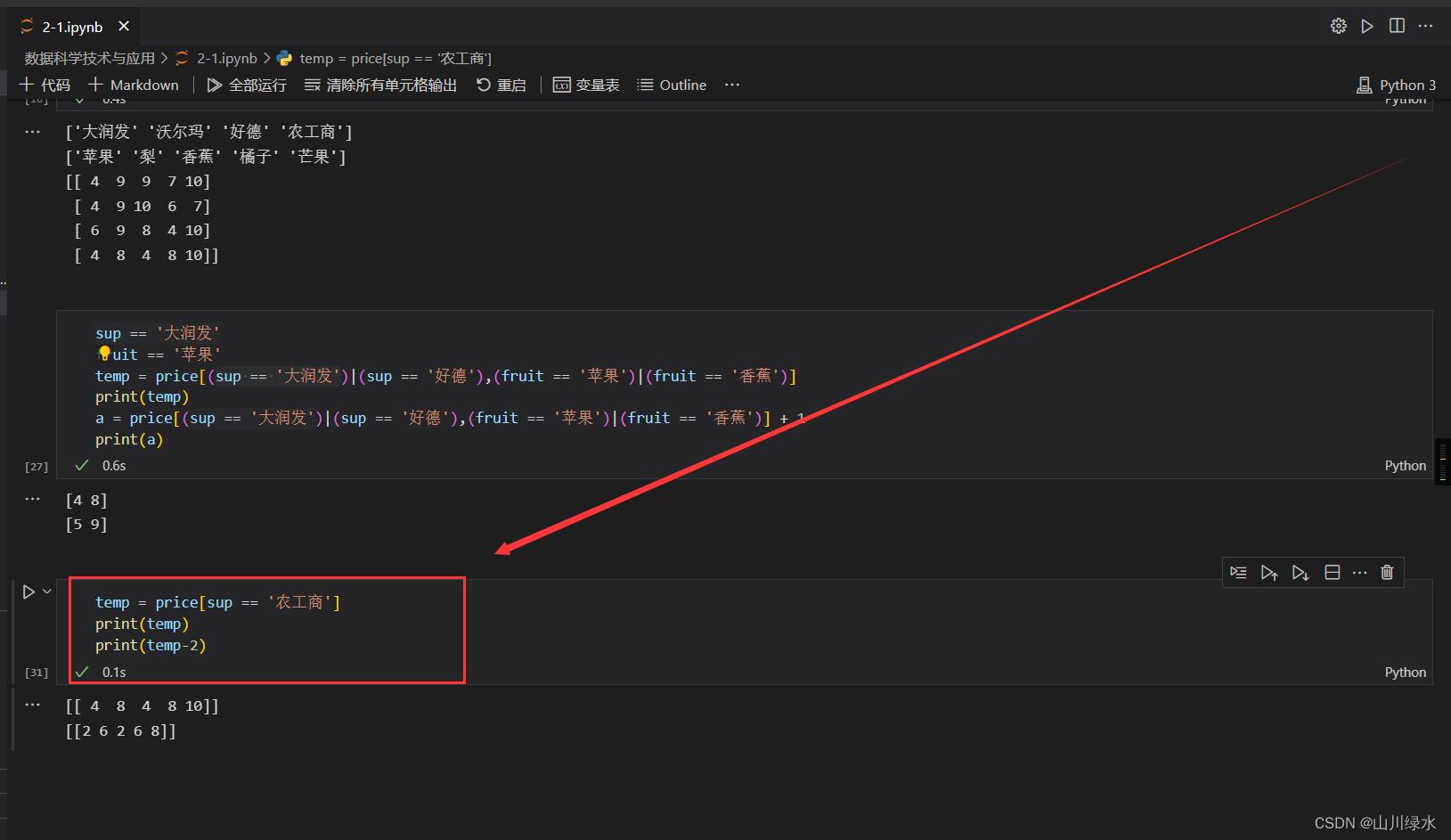
(4)农工商的水果大减价，将所有的水果价格减少2元。

temp = price[sup == '农工商']
print(temp)
print(temp-2)

(5)统计4个超市苹果和芒果的销售均价

price[sup == '大润发',fruit == '苹果']
price[sup == sup[0]]
for i in range(0,4):
      print(price[sup == sup[i],(fruit == '苹果')|(fruit == '芒果')].mean(axis=0))

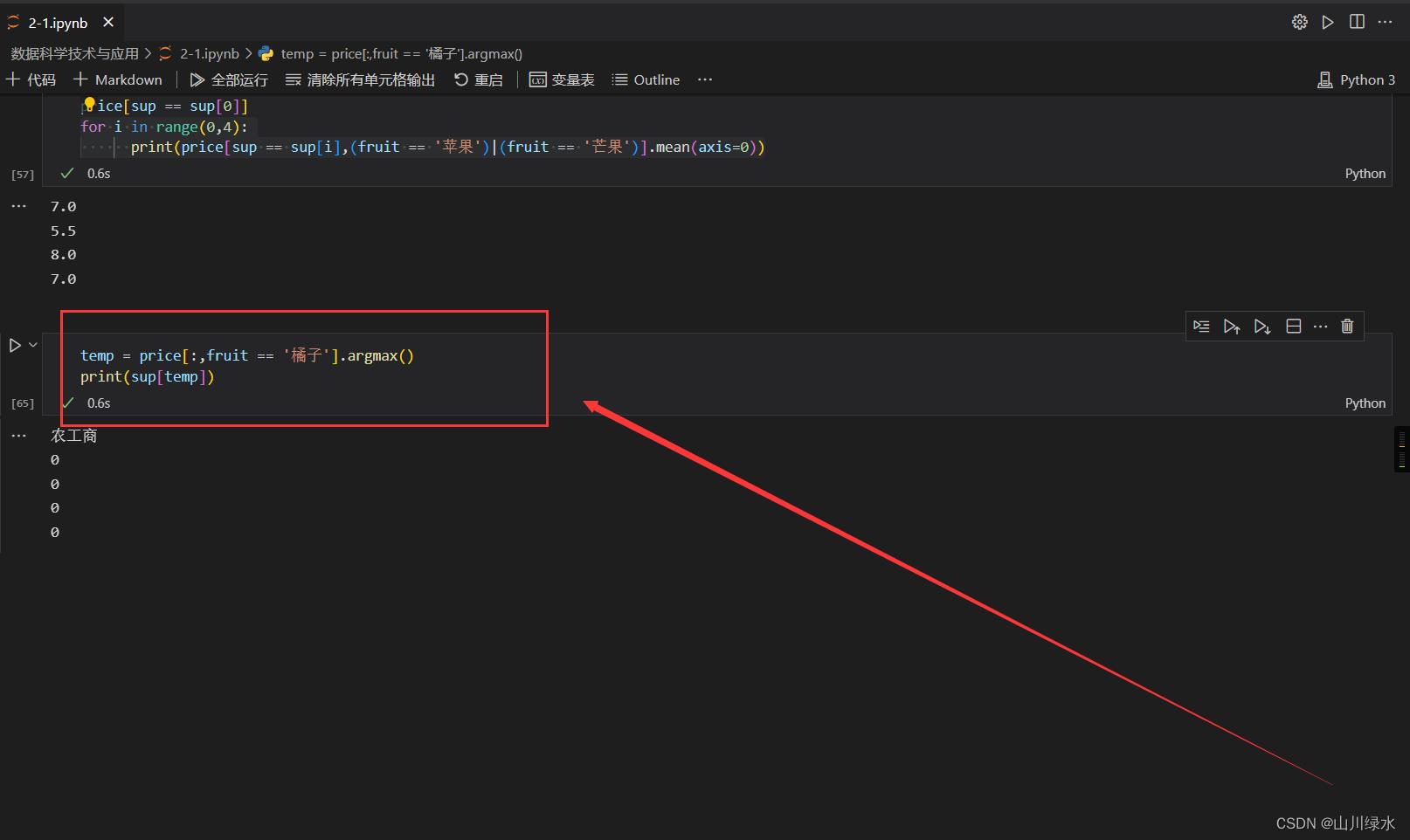
(6)找出橘子价格最贵的超市名称(不是编号)

temp = price[:,fruit == '橘子'].argmax()
print(sup[temp])

2.基于随机游走的例子，使用ndarray()和随机数生成函数模拟一个物体在三维空间游走的过程。

(1)创建3 x 10的二维数组，记录物体每步在三个轴上的移动距离。在每个轴向的移动距离服从正态分布（期望为0，方差为1）。行序0、1、2分别对应x轴，y轴、z轴。

temp = np.random.normal(0,1,size = (3,10))
temp

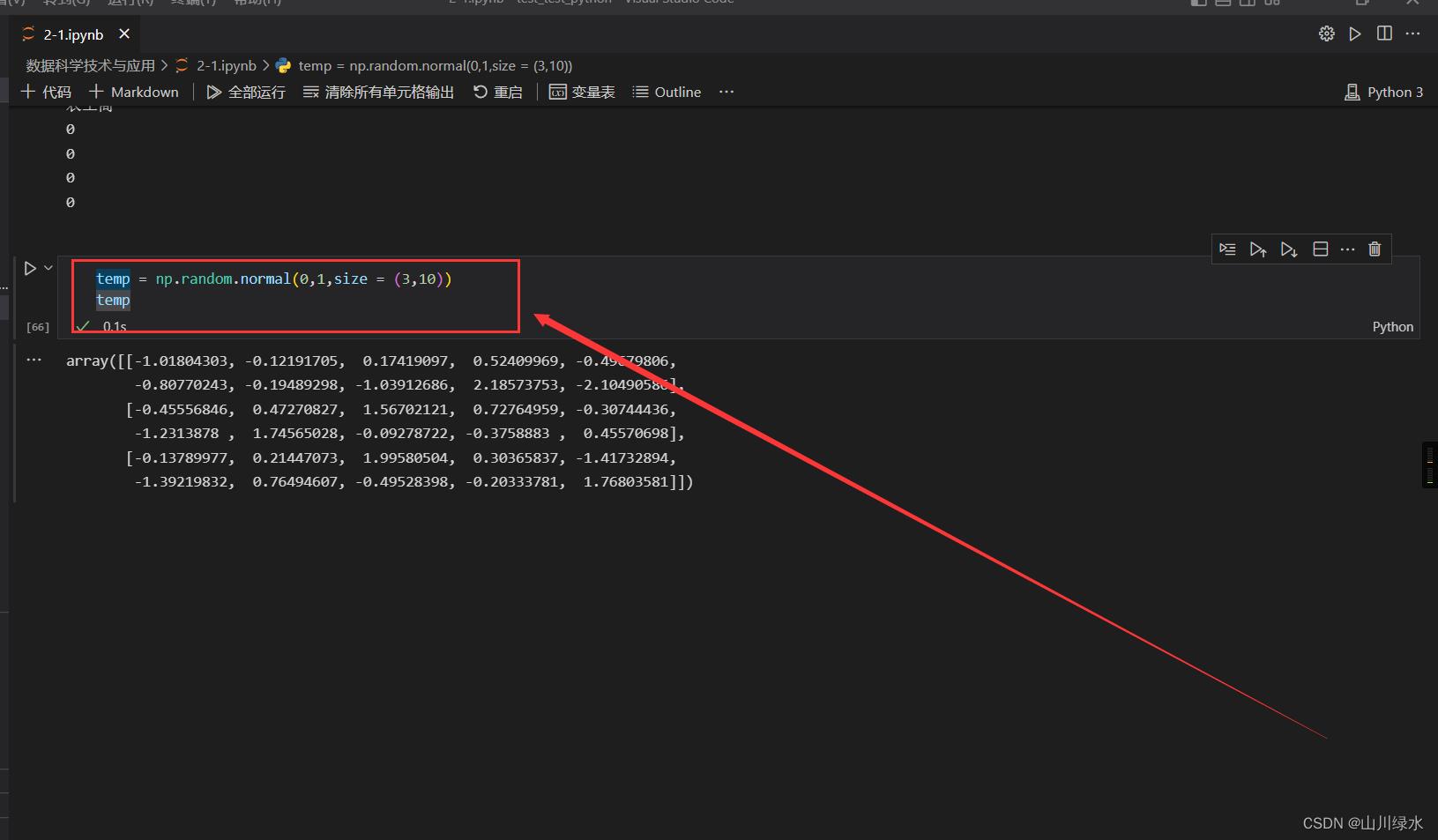
(2)计算每步走完后物体在三维空间的位置。

position = temp.cumsum(axis=1)
position

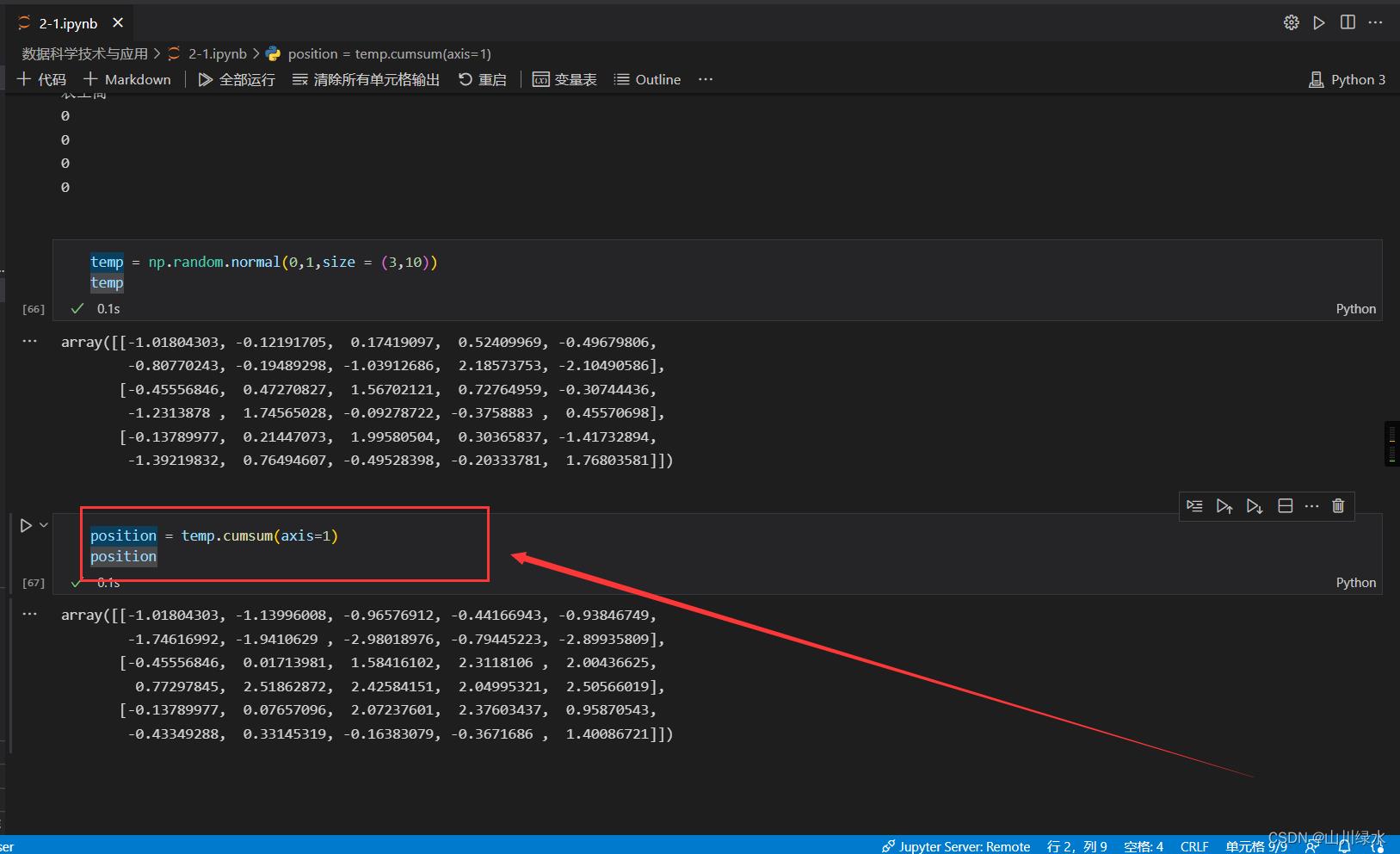
(3)计算每部走完后物体与原点的距离（只显示两位小数）

dists = np.sqrt(position[0]**2+position[1]**2+position[2]**2)
np.set_printoptions(precision=2)
dists

(4)统计物体在z轴上到达的最远距离。

max_dist = abs(position[2]).max()
max_dist

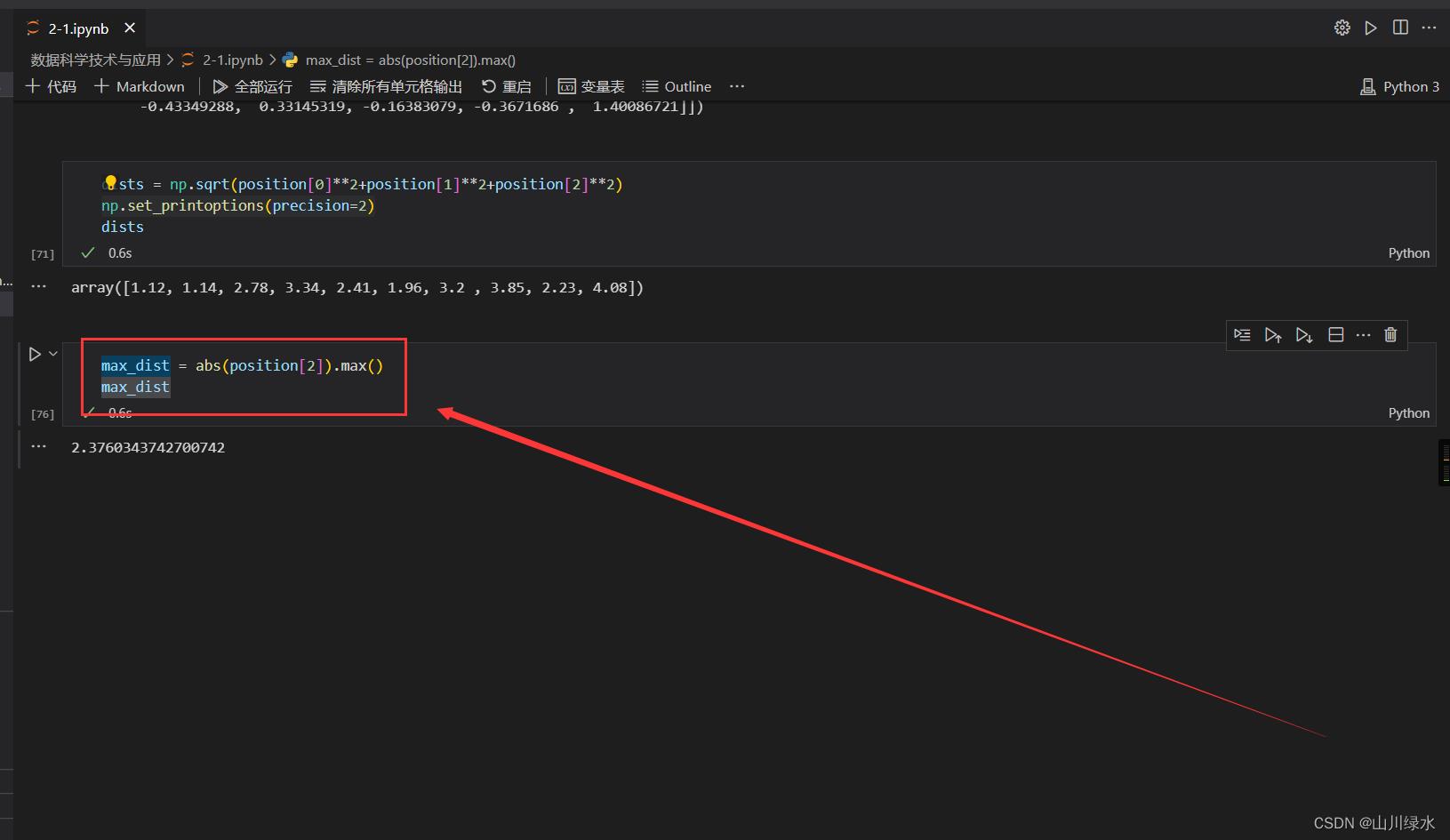
(5)统计物体在三维空间与原点距离的最近值

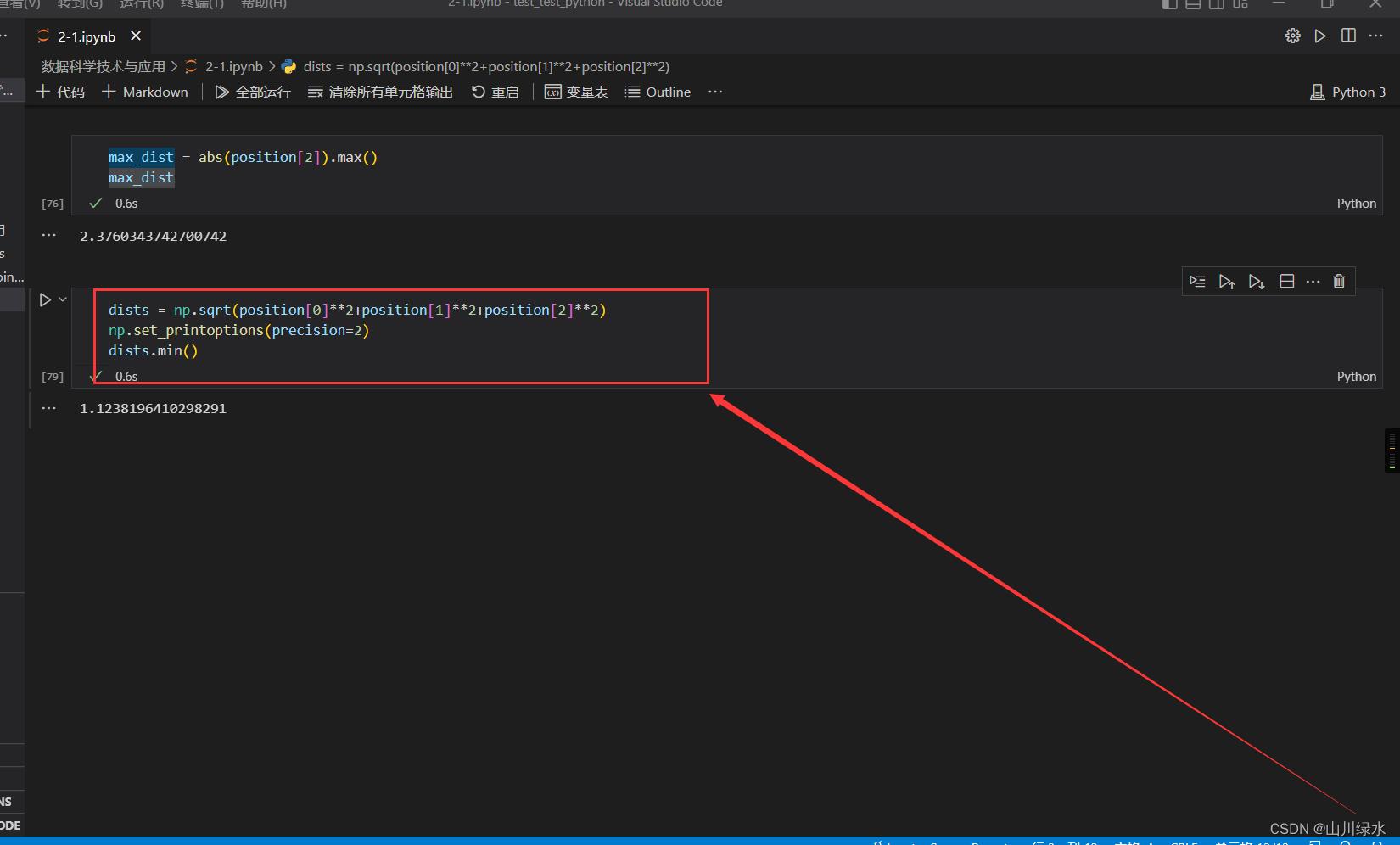
dists = np.sqrt(position[0]**2+position[1]**2+position[2]**2)
np.set_printoptions(precision=2)
dists.min()

以上是关于多维数据结构与运算的主要内容，如果未能解决你的问题，请参考以下文章

数据挖掘概念与技术--多维数据模型

UE4解决大地图问题（未完待续）

OpenCV学习笔记 008基于形态学运算的图像变换

python之numpy多维数组

形态学相关算子

数字图像处理图像开运算与闭运算

多维数据结构与运算

数据科学技术与应用——第2章 多维数据结构与运算

2.1 多维数据对象

例题如下

例题[2-1] 创建两个一维数组风别保存学生姓名和考试科目，访问数组元素。学业水平考试涉及多门课程和多名学生，虽然课程名称、姓名的数据类型都是字符串，但是对应的现实概念却不同，需存放两个一位数组中。

[例题2-2] 创建二维数组scores,记录names中每名学生对应subjects各门课程的考试成绩。

思考练习

1.一维数组访问

2.二维数组访问

3.生成有整数10~19组成的2 x 5的二维数组。

2.2 多维数组运算

例题如下

例题[2-3] 为所有学生的所有课程成绩增加5分

例题[2-4] 首先创建一维数组存放不同科目增加分数，然后将其和scores相加。

例题[2-5]将学生的考试成绩转换为整数形式的十分制分数

例题[2-6] 使用subtract()给每个学生的分数减去3分

例题[2-7] 按照分析目标使用聚合函数进行统计。

例题[2-8] 生成由10个随机整数组成的一维数组，整数的取值范围为0~5

思考与练习

1.将scores数组中所有学生的英语成绩减去3分并显示

2.统计scores数组中每名学生所有科目的平均分并显示

3.使用随机函数生成[-1,1]之间服从均匀分布的3 x 4的二维数组，并计算所有元素的和

2.3案例：随机游走轨迹模拟

1.模拟生成每步移动方向

2.计算每步移动后的位置

3.计算每步移动后与原点的距离

思考与练习

1.将随机游走的步数增加到100步，计算物体最终与原点的距离。

综合练习题

1.大润发、沃尔玛、好德和农工商4个超市售卖苹果、梨、香蕉、橘子和芒果5种水果。使用numpy的ndarray实现以下功能。

2.基于随机游走的例子，使用ndarray()和随机数生成函数模拟一个物体在三维空间游走的过程。

数据科学技术与应用——第2章多维数据结构与运算