七大排序扩展篇——Java
Posted 王嘻嘻-
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了七大排序扩展篇——Java相关的知识,希望对你有一定的参考价值。
目录
双向选择排序
思路:
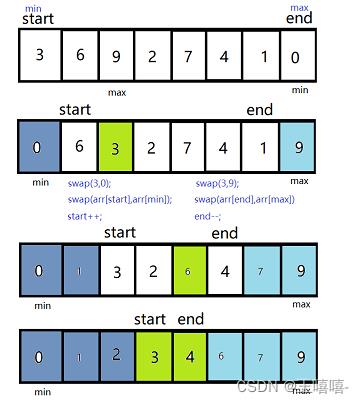
- 先定义min为首元素,max为尾元素,遍历数组;
- 如果遍历到的元素大于max,更新max;若元素小于min,更新min;
- 遍历一遍数组后,找到了最大值最小值下标;
- 将最小值与首部元素交换,最大值与尾部元素交换;
- 若最大值就是首部元素,在先将最小值与首部元素交换位置后,首部的最大值就被移动到最小值处,更新max=min,在进行与尾部元素交换。
源代码:
/**
* 双向选择排序
* 每趟同时保存最大和最小下标,设首位为最小,末尾为最大,从两头往中间不断对比交换,一趟就能够将两个数据归位。
**/
public class doubleSelectionSort
public void DoubleSelection(int[] arr, int start, int end)
while (start < end)
int min = start;
int max = end;
for (int i = start; i <= end; i++)
// 有大于 max 的数,更新 max
if (arr[max] < arr[i]) max = i;
// 有小于 min 的数,更新 min
if (arr[min] > arr[i]) min = i;
// 此时找到了最大值,最小值下标,交换最小值至首部,交换最大值至末尾
swap(arr, arr[start], arr[min]);
// 如果首部元素为最大值,首部元素先与最小值交换,首部最大值元素被交换到最小值,更新最大值下标
if (start == max) max = min;
swap(arr, arr[max], arr[end]);
++start;
--end;
// 交换
private void swap(int[] arr, int left, int right)
int temp = arr[left];
arr[left] = arr[right];
arr[right] = temp;
Quick Sort2 —— 二路快排
当数组中存在大量重复元素时,我们的快速排序又退化为了O(n^2)。之前的快速排序没有讨论等于arr[l]的情况,其中等于arr[l]的包含在大于等于中。
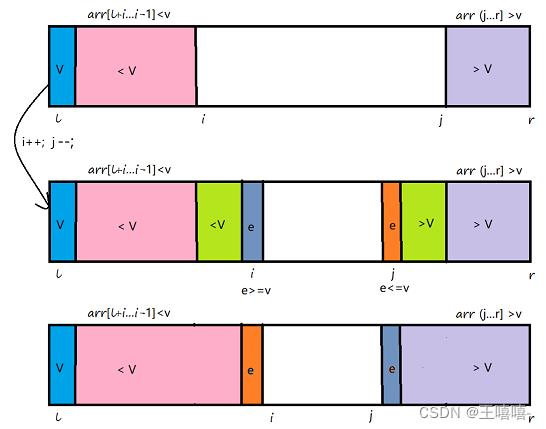
和单路快排不同的是 将数组中小于v和大于v的元素放在数组的两端,那么将引用新的索引 j 的记录大于v的边界位置
思路:
- 在数组中随机找一个元素 v ,将元素与首元素换位置,此时随机元素位于数组首部;
- 定义两个变量,i 指向首元素下一个位置,j 指向尾元素。i++, j-- 遍历数组;
- 当 i 的元素小于 v 时,i++,直到碰到了某个元素 >= v。j同理,直到碰到某个元素 <= v;
- 交换ij位置上的元素,继续i++,j-- 遍历数组;
- 将l和 j元素交换,此时j左边的元素都不大于j,右边的元素都不小于j;
- 此时就分别对j左边和j右边的元素进行二路快排。
源代码:
public class quickSortInternal2
public void quickSort(int[] arr, int n)
quickSort2(arr, 0 , n - 1);
// 二路快排
private void quickSort2(int[] arr, int l , int r)
if (l >= r) return;
int p = partition2(arr, l , r);
quickSort2(arr, l ,p - 1);
quickSort2(arr, p + 1, r);
// 维护两个索引i,j,分别从前往后,从后往前进行排序,交换
private static int partition2(int[] array, int l, int r)
// 随机选取待排序数组中的任意一个元素
int randomIndex = (int) (Math.random() * (r-l+1) + l);
// int randomIndex = (Math.abs(new Random().nextInt())%(r-l+1))+l;
swap(array, l , randomIndex);
int v = array[l];
int i = l + 1;
int j = r;
while (true)
while (i <= r && array[i] < v) i++;
while (j >= l + 1 && array[j] > v) j--;
if (i > j) break;
swap(array, i , j);
i++;
j--;
// 循环结束,j 下标为分区点位置
swap(array, l , j);
return j;
private static void swap(int[] array, int left, int right)
int temp = array[left];
array[left] = array[right];
array[right] = temp;
Quick Sort3 —— 三路快排
三路快排则是将数组分成了小于v,等于v,大于v的三个部分,当递归处理的时候,遇到等于v的元素不用管,只需要处理小于v,大于v的元素就好了。
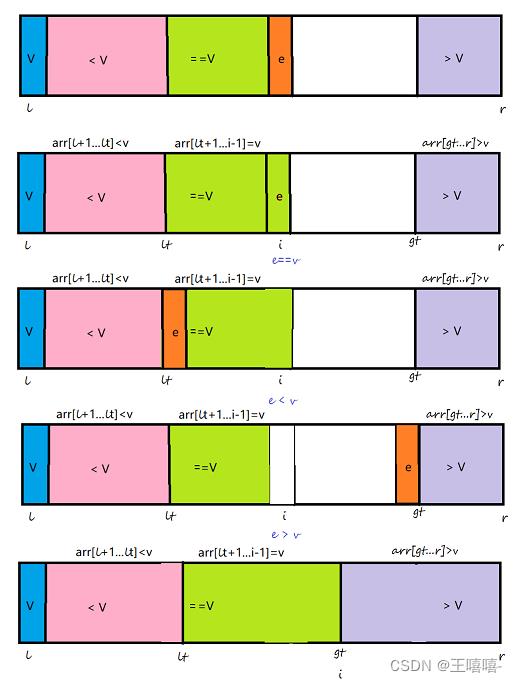
思路:
- 在数组中随机找一个元素 v ,将元素与首元素换位置,此时随机元素位于数组首部;
- 定义下标,i为首元素下一个位置,lt为首元素,gt为尾元素下一个;
- 遍历数组,e<v时,把当前元素e和==v部分的第一个元素进行交换,此时e这个元素就是<v部分最后一个元素,相应的lt这个索引需要向后移动一位。然后i++;
- "e>v",只需要把元素"e"和“gt-1”位置上的元素进行交换,相应的gt--。但是索引i不需要移动,依然指向一个没有被处理的元素,这个没有被处理过的元素是刚才从"gt-1"位置换过来的;
- 遍历完,将l的元素和lt交换即为分区点。分别对分区点左边和右边的元素排序。
源代码:
public class quickSortInternal3
private void quickSort3(int[] arr, int l, int r)
if (l >= r) return;
// 随机选取待排序数组中的任意⼀一个元素
int randomIndex = (int) (Math.random() * (r - l + 1) + l);
swap(arr, l ,randomIndex);
int v = arr[l];
// 定义并初始化下标索引,使得三部分区间为空
// arr[l+1...lt] < v
int lt = l;
// arr[lt+1,i] == v
int i = l + 1;
// arr[gt...r] > v
int gt = r + 1;
while (i < gt)
if (arr[i] < v)
swap(arr, i , lt + 1);
i++;
lt++;
else if (arr[i] > v)
swap(arr, i , gt - 1);
gt--;
else //arr[i] == v
i++;
// 循环走完只需要将l的元素和lt交换即为分区点
swap(arr, l , lt);
// 继续对 <v 部分进行快速排序
quickSort3(arr, l , lt - 1);
// 继续对 >v 部分进行快速排序
quickSort3(arr, gt , r);
// 交换
private void swap(int[] arr, int left, int right)
int temp = arr[left];
arr[left] = arr[right];
arr[right] = temp;
剑指offer 51、数组中的逆序对
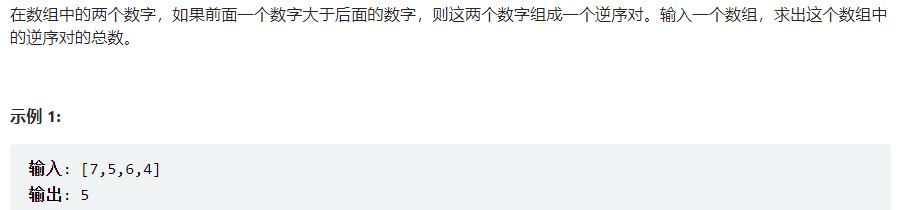
思路:
利用归并排序思想,先分成小分,合并的时候,i遍历比较左区间与右区间元素的值的大小。左区间的元素 < 右区间元素,不构成逆序对;右区间的元素 < 左区间的元素,构成逆序对,此时逆序对的个数 = mid - i + 1。
源代码:
class Solution
public int reversePairs(int[] nums)
return reversePairsHelper(nums,0,nums.length - 1);
/**
* 传入一个数组nums,就可以求出在nums[l,r]上的逆序对
* @param nums
* @param l
* @param r
* @return 此时nums[l,r]逆序对的个数
*/
private int reversePairsHelper(int[] nums, int l, int r)
if (l >= r)
return 0;
int mid = l + ((r - l) >> 1);
//先求出左区间的逆序对的个数
int left = reversePairsHelper(nums,l,mid);
//在求出右区间的逆序对的个数
int right = reversePairsHelper(nums,mid + 1,r);
if (nums[mid] > nums[mid + 1])
//排序好的左右区间还存在逆序对
return merge(nums,l,mid,r) + left + right;
return left + right;
/**
* 合并nums两个有序区间[l,mid] [mid + 1,r]
* 返回合并过程中逆序对的个数
* @param nums
* @param l
* @param mid
* @param r
* @return
*/
private int merge(int[] nums, int l, int mid, int r)
int[] aux = new int[r - l + 1];
// 合并过程中产生的逆序对个数
int ret = 0;
for (int i = 0; i < aux.length; i++)
aux[i] = nums[i + l];
int i = l;
int j = mid + 1;
for (int k = l; k <= r; k++)
if (i > mid)
// 左区间已经合并完毕,放入右区间元素
nums[k] = aux[j - l];
j ++;
else if (j > r)
// 右区间已经合并完毕,放入左区间元素
nums[k] = aux[i - l];
i ++;
else if (aux[i - l] <= aux[j - l])
// 左区间的元素 < 右区间元素,不构成逆序对
nums[k] = aux[i - l];
i ++;
else
// 右区间的元素 < 左区间的元素,构成逆序对
// 此时逆序对的个数 = mid - i + 1
ret += (mid - i) + 1;
nums[k] = aux[j - l];
j ++;
return ret;
以上是关于七大排序扩展篇——Java的主要内容,如果未能解决你的问题,请参考以下文章