2021-04-11

Posted 2022-11-14 差不多女生

文章目录

• 图像到图像的映射原理
• 一、单应性变换
• 二、仿射变换（affine）
• • 1.图像扭曲
  • 2.图中图
• 总结

---

图像到图像的映射原理

一、单应性变换

单应性变换（Homography）：单应性变换是将一个平面内的点映射到另一个平面内的二维投影变换。
公式1：

点的齐次坐标依赖于其尺度定义，因此单应性矩阵 H也仅依赖尺度定义，所以，单应性矩阵具有8个独立的自由度。

单应性矩阵可以由两幅图像中对应点计算出来。然后我们再得到坐标的变换公式。
将式1展开，用第三行除前两行，得到如下的式子：

得到：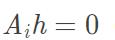
因为

所以由未知变量的个数可知，求解出H至少需要4对匹配点。通常情况下为了得到更稳定的结果，会用到多于4对的特征匹配。所以，这个方程会变成超定的，可以将最小二乘解作为最后的解。

二、仿射变换（affine）

仿射变换是计算机图形学中经常碰到的基本概念，它其实是线性变换和平移变换的叠加，可用于图像扭曲变形和图像配准
仿射变换保持了二维图形的“平直性”（直线经仿射变换后依然为直线）和“平行性”（直线之间的相对位置关系保持不变，平行线经仿射变换后依然为平行线，且直线上点的位置顺序不会发生变化）。非共线的三对对应点确定一个唯一的仿射变换。
仿射变换是线性变换后进行平移变换（其实也是齐次空间的线性变换），使用齐次坐标使得仿射变换可以以统一的矩阵形式进行表示。

仿射变换的数学表达形式为：
在这里插入图片描述其中 c1、c2控制平移，a1、a2、b1、b2控制旋转、缩放和剪切

因为单应性变换有8个自由度，仿射有6个自由度
仿射变换具有6个自由度，因此我们需要三个对应点来估计矩阵，通过将最后两个元素设置为0，即h7=h8=0，仿射变换可以用DLT算法估计得出。

1.图像扭曲

from array import array
from statistics import mean

from matplotlib._layoutbox import vstack
from numpy import *
from matplotlib.pyplot import *
from numpy import diag, dot, concatenate, zeros
from numpy.core import ones, std
from scipy import ndimage, linalg
from PIL import Image

im = array(Image.open('1.jpg').convert('L'))
H = array([[1.4,0.05,-100],[0.05,1.5,-100],[0,0,1]])
im2 = ndimage.affine_transform(im, H[:2,:2],(H[0,2],H[1,2]))

gray()
subplot(121)
imshow(im)
axis('off')
subplot(122)
imshow(im2)
axis('off')
show()

原图：

扭曲效果:

2.图中图

from array import array
from statistics import mean

from matplotlib._layoutbox import vstack
from numpy import *
from matplotlib.pyplot import *
from numpy import diag, dot, concatenate, zeros
from numpy.core import ones, std
from scipy import ndimage, linalg
from PIL import Image



def Haffine_from_points(fp, tp):
    """计算H仿射变换，使得tp是fp经过仿射变换H得到的"""

    if fp.shape != tp.shape:
        raise RuntimeError('number of points do not match')

    # 对点进行归一化（对数值计算很重要）
    # --- 映射起始点 ---
    m = mean(fp[:2], axis=1)
    maxstd = max(std(fp[:2], axis=1)) + 1e-9
    C1 = diag([1 / maxstd, 1 / maxstd, 1])
    C1[0][2] = -m[0] / maxstd
    C1[1][2] = -m[1] / maxstd
    fp_cond = dot(C1, fp)

    # --- 映射对应点 ---
    m = mean(tp[:2], axis=1)
    C2 = C1.copy()  # 两个点集，必须都进行相同的缩放
    C2[0][2] = -m[0] / maxstd
    C2[1][2] = -m[1] / maxstd
    tp_cond = dot(C2, tp)

    # 因为归一化后点的均值为0，所以平移量为0
    A = concatenate((fp_cond[:2], tp_cond[:2]), axis=0)
    U, S, V = linalg.svd(A.T)

    # 如Hartley和Zisserman著的Multiplr View Geometry In Computer,Scond Edition所示，
    # 创建矩阵B和C
    tmp = V[:2].T
    B = tmp[:2]
    C = tmp[2:4]

    tmp2 = concatenate((dot(C, linalg.pinv(B)), zeros((2, 1))), axis=1)
    H = vstack((tmp2, [0, 0, 1]))

    # 反归一化
    H = dot(linalg.inv(C2), dot(H, C1))

    return H / H[2, 2]

def image_in_image(im1, im2, tp):
    """使用仿射变换将im1放置在im2上，使im1图像的角和tp尽可能的靠近
        tp是齐次表示的，并且是按照从左上角逆时针计算的"""

    # 扭曲的点
    m, n = im1.shape[:2]
    fp = array([[0, m, m, 0], [0, 0, n, n], [1, 1, 1, 1]])

    # 计算仿射变换，并且将其应用于图像im1中
    H = Haffine_from_points(tp, fp)
    im1_t = ndimage.affine_transform(im1, H[:2, :2],
                                     (H[0, 2], H[1, 2]), im2.shape[:2])
    alpha = (im1_t > 0)

    return (1 - alpha) * im2 + alpha * im1_t

im1 = array(Image.open('2.jpg').convert('L'))
im2 = array(Image.open('1.jpg').convert('L'))

gray()
subplot(131)
imshow(im1)
axis('equal')
axis('off')
subplot(132)
imshow(im2)
axis('equal')
axis('off')

# 选定一些目标点
tp = array([[164, 338, 580, 364], [60, 26, 505, 405], [1, 1, 1, 1]])

im3 = image_in_image(im1, im2, tp)
subplot(133)
imshow(im3)
axis('equal')
axis('off')
show()

原图：


效果图：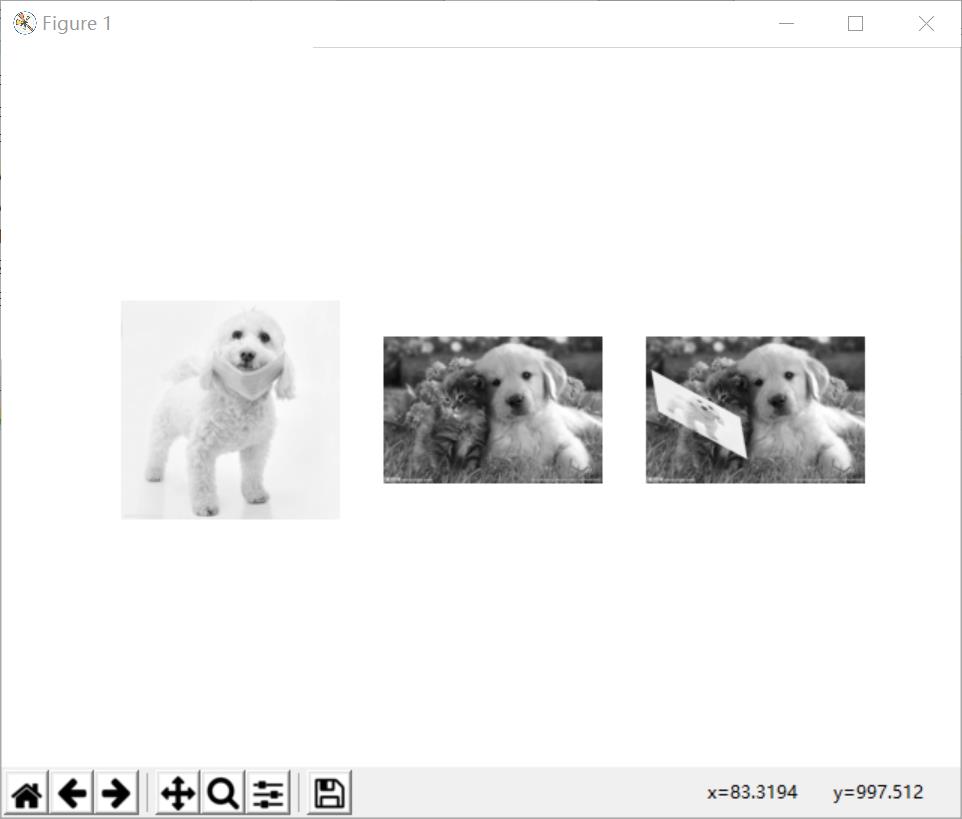

总结

本次实验中通过学习单应性变换，知道了单应性矩阵主要解决两个问题：
1.表述真实世界中一个平面与对应它图像的透视变换
2.从通过透视变换实现图像从一种视图变换到另外一种视图
仿射变换它可以通过一系列原子变换的复合来实现，其中包括:平移
(Translation)、缩放(Scale)、旋转(Rotation)、翻转(Flip)和错切(Shear)五种。不共线的三对对应点决定了-一个唯一 一的仿射变换。 仿射变换保持了二维图形的“平直性”（直线经仿射变换后依然为直线）和“平行性”（直线之间的相对位置关系保持不变，平行线经仿射变换后依然为平行线，且直线上点的位置顺序不会发生变化）。