arkworks零知识证明库学习资料

Posted 2022-11-13 Anyanyamy

零知识证明基础

一、基础概念

1. 椭圆曲线

【参考】

https://andrea.corbellini.name/2015/05/17/elliptic-curve-cryptography-a-gentle-introduction/

实数域上的椭圆曲线的定义：

  

 群Group：满足以下特性：

1. closure：a,b属于G，则a+b属于G

2. associativity：(a+b)+c = a+(b+c)

3. identity element：存在单位元0，使得a+0=0+a=a

4. 每个元素存在逆元inverse：使得a+b=0

群额外还有性质：1. 单位元唯一 2. 逆元唯一

如果还满足5. a+b=b+a，则称为abelian group阿贝尔群。

整数集合Z就是阿贝尔群。

The group law for elliptic curves 定义椭圆曲线上的群

1. 群中元素即椭圆曲线上的点

2. 单位元是无穷远点0

3. 点P的逆元是关于x轴对称的点

4. 加法：三个一条线上的非0点之和为0

     

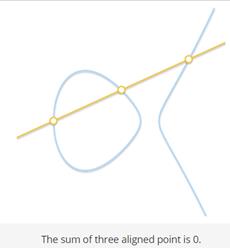
  这样就可以在椭圆曲线上完成加法操作，可以想象成打点操作

2. 有限域下的椭圆曲线

【参考】

https://andrea.corbellini.name/2015/05/23/elliptic-curve-cryptography-finite-fields-and-discrete-logarithms/

The field of integers modulo p 模p的有限域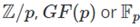  

p为prime素数，其中定义了模p的加法和乘法，包含的元素从0,1, … p-1

除法操作等同于乘以元素的逆元

定义在有限域上的椭圆曲线公式如下，a, b也是Fp中的元素，操作也都要mod p

  图中的点的x，y都是mod p的值，关于y=p/2对称，这些点仍构成阿贝尔群。

这时的加法在超出边界后会从对面继续穿出来。

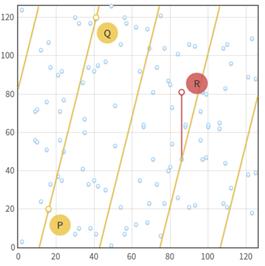
 The order of an elliptic curve group定义在有限域上的椭圆曲线所包含点的数目称为阶。

点P的阶是满足nP=0的最小正数n，并且这个n是大群的阶的因子。

the order of P is the smallest positive integer n such that nP=0.

the order of a subgroup is a divisor of the order of the parent group.

二、BLS12-381

1. 基本介绍

BLS12-381是一种Zcash中所使用的新型zk-SNARK椭圆曲线加密算法，隶属于Bellman库，由Rust语言所实现，它的特点是小巧易用，能快速验证，同时兼备加密时延和快速可验证两个特性。可缩小算术电路的大小，降低密钥的大小，以及简化协议。

BLS12-381的一些参数：

① 嵌入度embedding degree：12

 ② number of bits needed to represent coordinates on the curve: the field modulus, q：381，

即有限域Fq的q的位数是381位

③ 安全级别：约等于128位

④ group order 群的阶：约等于2^256，不是质数

it is not a prime, you have generators of different orders (which all divide the curve order)

⑤ 私钥：Fq上的一个值x，其长度为381 bit。

【参考】https://blog.csdn.net/mutourend/article/details/92784689?utm_medium=distribute.pc_relevant.none-task-blog-2%7Edefault%7EBlogCommendFromMachineLearnPai2%7Edefault-4.control&depth_1-utm_source=distribute.pc_relevant.none-task-blog-2%7Edefault%7EBlogCommendFromMachineLearnPai2%7Edefault-4.control

实际上用了两条曲线，这里先介绍简单的一条G1

【参考】 https://tools.ietf.org/id/draft-yonezawa-pairing-friendly-curves-02.html#rfc.section.4.2.2

x：用于计算p, r，需要满足一些条件，目前 

 p：有限域的参数，即椭圆曲线上的点坐标都要mod p，是381位的

r：子群G1的阶，即点的总个数

G：base point（BP），是群的生成元。

h: A subgroup’s cofactor is the ratio of the size of the whole group to the size of the subgroup.

大群的阶/子群的阶

a, b：方程的系数

2. 具体参数

 

另一条复杂曲线G2的参数如下：

 

 

 

其实BLS12-381使用了两条曲线，第一条就是上面介绍的比较简单的G1。第二条是拓展的曲线G2，可以想象成复数域上的。可以映射到GT，用于后面的双线性映射

 

 

 

BLS12-381中的第一条椭圆曲线G1中的点为P，第二条椭圆曲线G2中的点为Q。

双线性映射e: G1 ×  G2 -> GT。

【参考】 https://hackmd.io/@benjaminion/bls12-381

【参考】https://crates.io/crates/bls12_381

三、arkworks库解读

1. Fp, Fq, Fr

ark-bls12-381 中定义第一条椭圆曲线G1使用的有限域

Fr是有限域的别名，Fp256是个结构体，其中使用泛型，里面的结构体类型为FrParameters

结构体FrParameters实现了3个trait：Fp256Parameters, FftParameters和FpParameters

MODULUS是G1的阶r

在ark-ff中实现了Fp256结构体的定义与Fp256Parameters这个trait的定义。可以用4Byte的BigInteger来实现Fp256的有限域。类似的也定义了Fp384和Fp384Parameters。

 

 

 

  

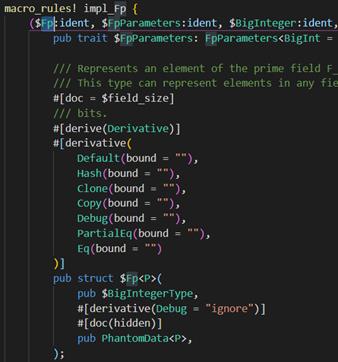
定义FftParameters这个trait，定义了用于FFT的参数

 

 

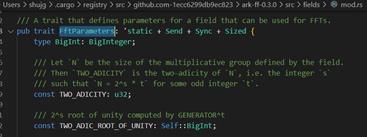
定义FpParameters这个trait，定义了素数域的参数

 

 

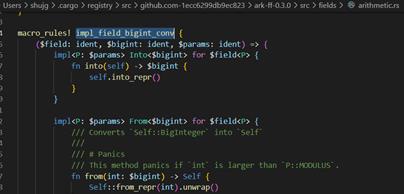
实现BigInteger和field的转换，即BigInteger256可以利用Fp256Parameters转到Fp256中

 g1.rs中定义了G1的参数，包括cofactor等，定义椭圆曲线上的点

 定义第二条椭圆曲线G2使用的有限域Fq，类似的可以把Fq看作一个有限域的结构体

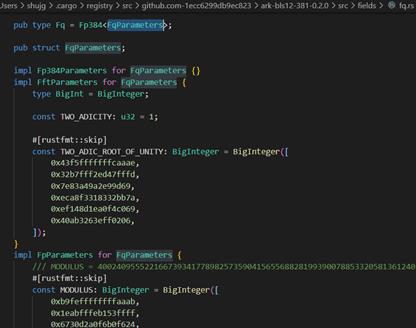
类似的，g2.rs中定义了G2的参数，包括cofactor等，定义的是椭圆曲线上的点

2. 变量分配

ark-r1cs-std中

AllocatedFp<F>结构体：在约束系统中表示域中元素的变量

FpVar<F>枚举类型：在有限域F中的变量，可以是约束系统CS中的常量，也可以是CS中分配的变量。两个类型都实现了AllocVar trait，这个trait提供三种CS里的分配方式。

 

 

   

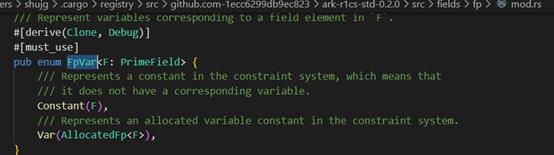
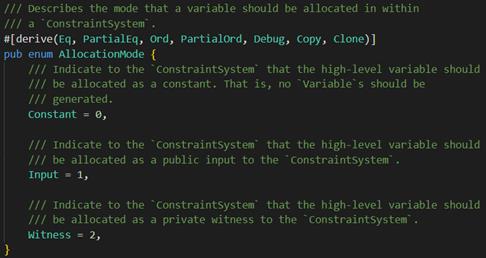
AllocVar这个trait中定义了三种CS中分配的形式：

Constant：在CS中不创建变量

Input：公开输入，Prover和Verifier都知道

Witness：私密输入，只有Prover知道

 

 

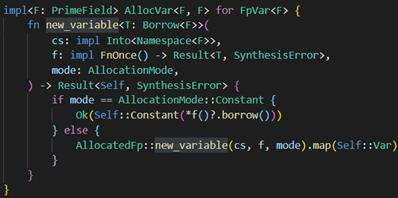
i64的数据首先通过into转到Fp有限域中，可以是Fp256，也可以是Fp384；

然后通过FpVar<F>的函数转到CS中。

 实际上调用的还是AllocatedFp::new_variable

 

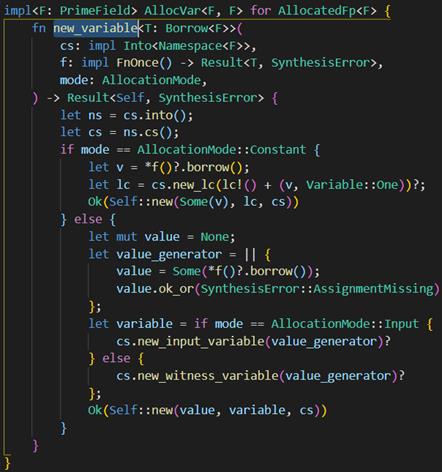
再往下调用的是约束系统CS的创建函数

所有用于零知识证明的结构体都需要实现ContraintSynthesizer这个trait，即手动实现generate_contraints函数

 ConstraintSystem结构体：用来描述R1CS，在分配变量时本质上调用的是这里的函数。

Constant调用的是new_lc，本质上调用了Variable::SymbolicLc

Input调用的是new_input_variable，本质上调用了Variable::Instance

Witness调用的是new_witness_variable，本质上调用了Variable::Witness

 

  

 

 

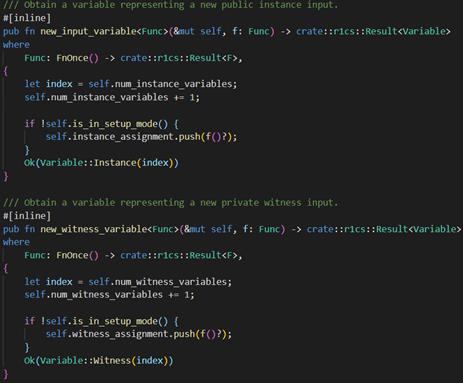
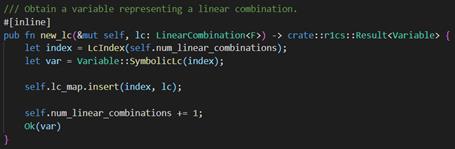
再看Variable其实是枚举类型，所以分配变量最终是创建了三种类型的Variable

 

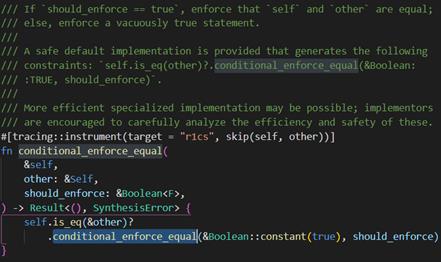
在创建完变量后进行约束：

enforce_equal，但这个函数似乎可有可无