统计学上的几个概念

Posted 2022-11-09 1501220038

总是隔一段时间就忘，还是记下来。

均值：一组数求平均。可以是正数、负数或0

方差(差的平方求均值)：各数与均值之间差的平方，求和除以元素个数（注意excel中的方差和标准差函数均分为总体和样本两种，区别是除以n还是n-1）。方差一定是正数或者0。

标准差：方差开平方，取正平方根。

协方差：用于表示两组数的相关性——A组数的各个元素和其均值的差乘以B组数的各个元素和其均值的差，求和后再除以元素个数。是两组数计算后得到一个数。这个数为正数表示趋向正相关，为负数趋向于负相关。为0是不相关。
其原理是：如果A组数的元素1大于其均值，而B组数的元素1也大于其均值，那么相乘结果>0；同理如果都小于均值，相乘结果也>0。如果一个大于一个小于，相乘结果就<0。类似元素2，元素3…元素n都是如此。那么如果同时大于均值或者小于均值的情况比较多，乘出来的正数就比较多，最后取和的结果也倾向于正数。如果一个大于均值一个小于均值的情况比较多，乘出来的负数就比较多，最后取和的结果也倾向于负数。

协方差矩阵：协方差只能表示两组数据的关系，如果是在多组数据中找关系，就需要两两组合的去算协方差。这样最后就组成一个协方差矩阵。所以矩阵对角线上就是各组数据的方差（自己与自己的协方差就是这组数的方差）；而且协方差矩阵一定是依对角线对称（因为A与B的协方差等于B与A的协方差）。
协方差矩阵算法除了上面说的两两计算协方差后填入数据。还可以这样计算：每组数的各个元素均减去本组的均值（即使每组数的均值都为0），得到一个中心化的新矩阵，用这个矩阵乘以它的转置，再除以元素个数。

相关系数：因为协方差是一个数，而且可大可小。但是因为和元素本身的数值大小有关系，所以并不能直观体现相关的程度。所以在协方差基础上再除以两组数各自标准差的乘积，得到的就是皮尔逊相关系数。相关系数的取值范围在-1到1之间。这样观察和比较相关性就直观多了。

相关系数矩阵：同样的，相关系数矩阵也是两两计算而来。矩阵对角线上总是1（自己与自己完全正相关）

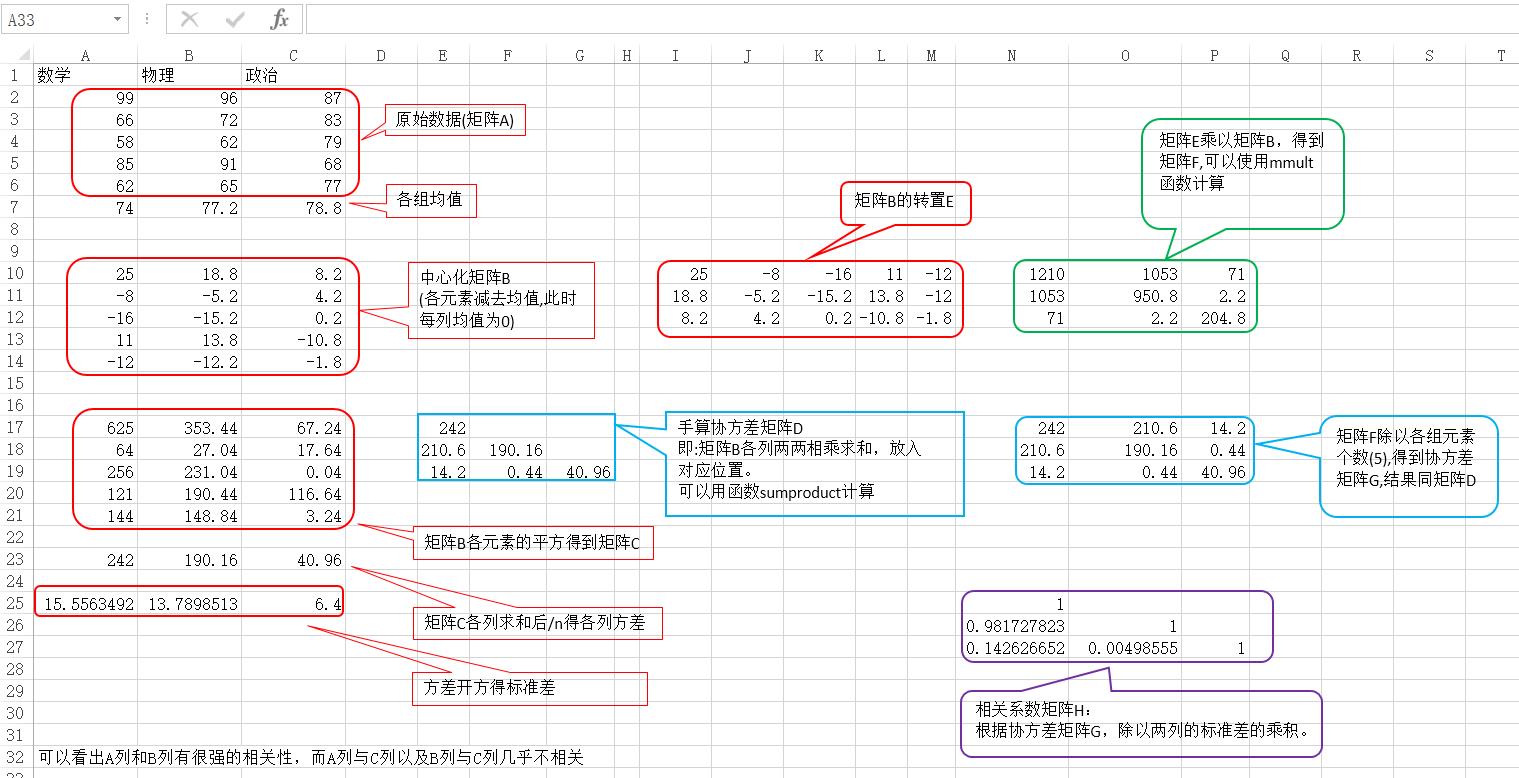
excel2010版之后提供数据分析功能，启用此功能在选项-加载项-转到-勾选。数据分析里包含了相关计算，结果是等同的。

t检验：待续