理解编辑距离算法

Posted 2022-11-05 言成言成啊

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了理解编辑距离算法相关的知识，希望对你有一定的参考价值。

一、理解

1.1 场景

当百度搜索错误时，下方会有提示，你要找的是不是xxx？

这样的一个功能是怎么实现的呢？

从最简单的思路出发，维护一套关键词词库，当搜索时，去与词库比较，哪一个最相似即可。

关键就在于最相似，如何实现？这就需要编辑算法了。

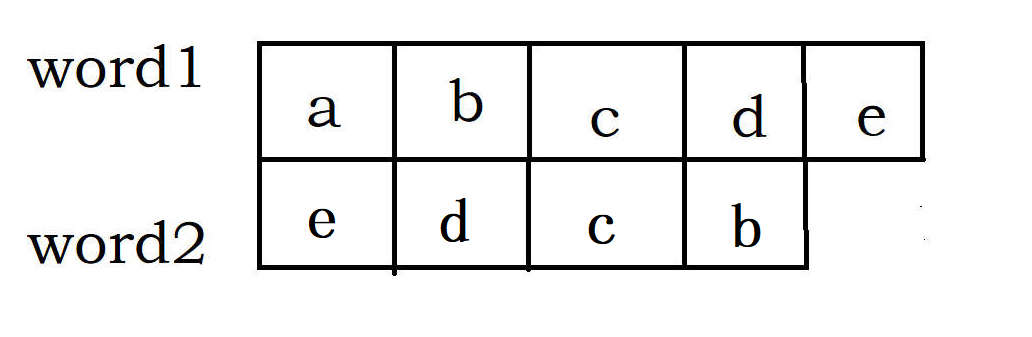
每步只能执行如下3个操作中的一个，

插入一个字符
删除一个字符
替换一个字符

将如图的word1换成word2最少需要几步。这就是编辑算法。

1.2 递归解法

求word1转换成word2最少步骤的基本思路

若word1[m]==word2[n]，则继续比较word1[0…m-1]与word[0…n-1]的结果。
若word1[m]!=word2[n]，则选择下面三个选项中最小的那个加1(表示进行了一次替换)
- 对word1尾部执行插入相同字符操作，work1与word2尾部抵消掉，比较word1[0…m]与word2[0…n-1]
- 对word1尾部执行删除字符操作，比较word1[0…m-1]与word2[0…n]
- 对word1尾部执行替换成word2相同字符操作，抵消掉，比较word1[0…m-1]与word[0…n-1]

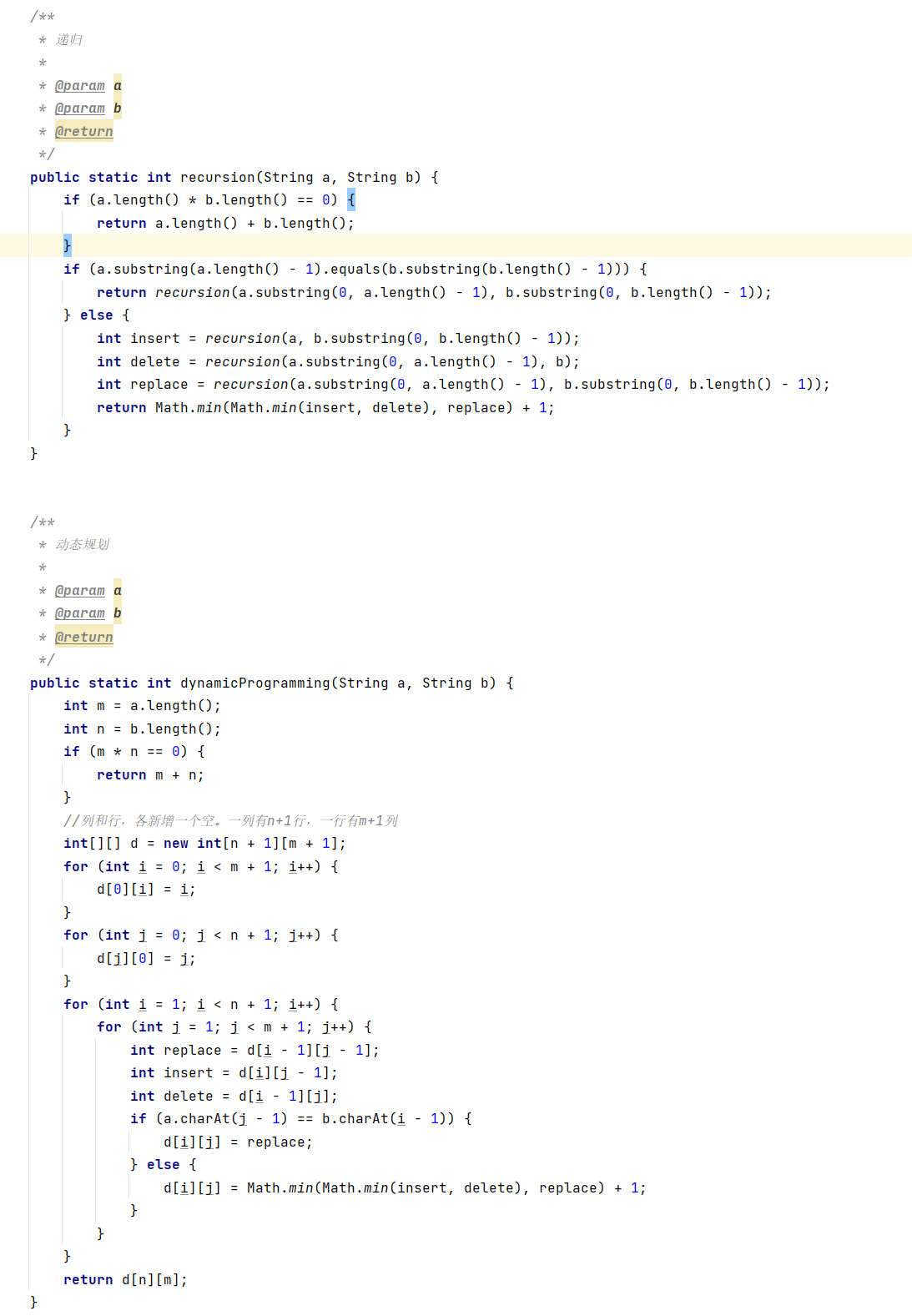
下面是递归实现

/**
 * 递归
 *
 * @param a
 * @param b
 * @return
 */
public static int recursion(String a, String b) 
    if (a.length() * b.length() == 0) 
        return a.length() + b.length();
    
    if (a.substring(a.length() - 1).equals(b.substring(b.length() - 1))) 
        return recursion(a.substring(0, a.length() - 1), b.substring(0, b.length() - 1));
     else 
        int insert = recursion(a, b.substring(0, b.length() - 1));
        int delete = recursion(a.substring(0, a.length() - 1), b);
        int replace = recursion(a.substring(0, a.length() - 1), b.substring(0, b.length() - 1));
        return Math.min(Math.min(insert, delete), replace) + 1;

需要理解，一旦涉及子问题，可以使用自顶向下的递归，或者，自底向上的动态规划。

1.3 动态规划解法

想要使用动态规划，先要抽象出状态转移方程。

word1与word2是两个对应的状态，所以一定是二维状态数组。

抽象出状态转移方程

如果word1[i]==word2[j]，那么dp[i][j]=dp[i-1][j-1]
否则，dp[i][j]=1+min(dp[i][j-1], dp[i-1][j], dp[i-1][j-1])

dp表示dynamicProgramming

动态规划实现如下

/**
 * 动态规划
 *
 * @param a
 * @param b
 * @return
 */
public static int dynamicProgramming(String a, String b) 
    int m = a.length();
    int n = b.length();
    if (m * n == 0) 
        return m + n;
    
    //列和行，各新增一个空。一列有n+1行，一行有m+1列
    int[][] d = new int[n + 1][m + 1];
    for (int i = 0; i < m + 1; i++) 
        d[0][i] = i;
    
    for (int j = 0; j < n + 1; j++) 
        d[j][0] = j;
    
    for (int i = 1; i < n + 1; i++) 
        for (int j = 1; j < m + 1; j++) 
            int replace = d[i - 1][j - 1];
            int insert = d[i][j - 1];
            int delete = d[i - 1][j];
            if (a.charAt(j - 1) == b.charAt(i - 1)) 
                d[i][j] = replace;
             else 
                d[i][j] = Math.min(Math.min(insert, delete), replace) + 1;
            
        
    
    return d[n][m];