悟透Qt—求解画布经任意中心点旋转后相对旋转前坐标系的坐标

Posted 2022-11-04 itzyjr

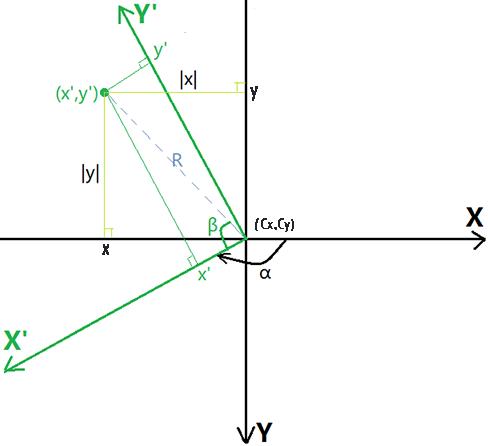
黑色坐标系是旋转前的画布坐标，画布以中心点(Cx,Cy)顺时针旋转 α 角度后，就变换成了绿色坐标系。
在经旋转后的绿色坐标坐中任取一点(x’,y’)，现求出(x’,y’)在旋转前黑色坐标系中的坐标值。

|x| = R * cos(π*3/2 - α - β) = -R * cos(α + β)
|y| = R * sin(π*3/2 - α - β) = -R * sin(α + β)
 x' = R * cos(β)
 y' = R * sin(β)
 
|x| / x' = -cos(α + β) / cos(β)
|y| / y' = -sin(α + β) / sin(β)

|x| / x' = -cos(α) + sin(α) * tan(β) = -cos(α) + sin(α) * y'/x';
|y| / y' = -sin(α) * cot(β) - cos(α) = -sin(α) * x'/y' - cos(α)

|x| = -cos(α) * x' + sin(α) * y'
|y| = -sin(α) * x' - cos(α) * y'

➊旋转中心点(Cx,Cy)=(0,0)
由于|x|在黑色坐标系中心点左侧、|y|在黑色坐标系中心点上侧，所以它们都是向值减小的方向(负方向)，取负值，即：

x = cos(α) * x' - sin(α) * y'
y = sin(α) * x' + cos(α) * y'

同时，也可以得出：
x' =  cos(α) * x + sin(α) * y = cos(-α) * x - sin(-α) * y
y' = -sin(α) * x + cos(α) * y = sin(-α) * x + cos(-α) * y

即，顺时针(因Y轴朝下)旋转 α 角，就从(x',y')旋转到(x,y)；反之，逆时针旋转 α 角(顺时针旋转 -α 角)，就是从(x,y)旋转到(x',y')。

用矩阵表示为：（绕Z轴顺时针(因为Y轴向下)旋转α度的2x2旋转矩阵）
$$\left(\begin{array}{l}x\\ y\end{array}\right)=\left[\begin{array}{ll}cos\alpha & -sin\alpha \\ sin\alpha & cos\alpha \end{array}\right]\times \left(\begin{array}{l}{x}^{\prime }\\ y^{\prime }\end{array}\right)$$
即，画布经顺时针(因为Y轴向下)旋转 α 角度后在新的坐标系下的坐标(x’,y’)，它在旋转前的坐标系下的坐标：(x,y)=[旋转矩阵]●(x’,y’)。

用Qt代码验证一下：

    float angle = 90 或 180;// 这两个值最容易在脑海中去验证
    float radians = qDegreesToRadians(angle);
    float rotElems[] =  qCos(radians), -qSin(radians),// in row-major order
                         qSin(radians), qCos(radians) ;
    QMatrix2x2 rotMat(rotElems);
//    rotMatrix(0, 0) = qCos(radians);
//    rotMatrix(0, 1) = -qSin(radians);
//    rotMatrix(1, 0) = qSin(radians);
//    rotMatrix(1, 1) = qCos(radians);
    float pointxy[] = 12.34, 67.89;
    QGenericMatrix<1, 2, float> pointMat(pointxy);
    auto rotPoint = rotMat * pointMat;// 矩阵乘法
    qDebug() << rotPoint;

当angle=90时，公式满足(x,y)=(-y’,x’)，打印结果是QGenericMatrix<1, 2, float>(-67.89 12.34)，验证通过。
当angle=180时，公式满足(x,y)=(-x’,-y’)，打印结果是QGenericMatrix<1, 2, float>(-12.34 -67.89)，验证通过。
其中，脑海中相像一下黑色坐标系旋转90°、180°的情况，很容易知道是什么轴和什么轴方向互换或者反向了。实际上，使用其他任何角度值，也都能通过验证。

➋旋转中心点(Cx,Cy)为任意值时的旋转矩阵
前面已经推导出：

|x| = -cos(α) * x' + sin(α) * y'
|y| = -sin(α) * x' - cos(α) * y'
那么：
x = Cx - |x| = (cos(α) * x' - sin(α) * y') + Cx
y = Cy - |y| = (sin(α) * x' + cos(α) * y') + Cy

可以看到，就是经过一次平移变换，这时在矩阵上加上平移变换，就不能是2x2矩阵了，得是3x3矩阵，如下：
$$\left[\begin{array}{lll}cos\alpha & -sin\alpha & Cx\\ sin\alpha & cos\alpha & Cy\\ 0& 0& 1\end{array}\right]$$
$$\left(\begin{array}{l}x\\ y\\ 1\end{array}\right)=\left[\begin{array}{lll}cos\alpha & -sin\alpha & Cx\\ sin\alpha & cos\alpha & Cy\\ 0& 0& 1\end{array}\right]\times \left(\begin{array}{l}{x}^{\prime }\\ y^{\prime }\\ 1\end{array}\right)$$
➌旋转中心点(Cx,Cy)不是画布的中心点而是任意点时的旋转矩阵

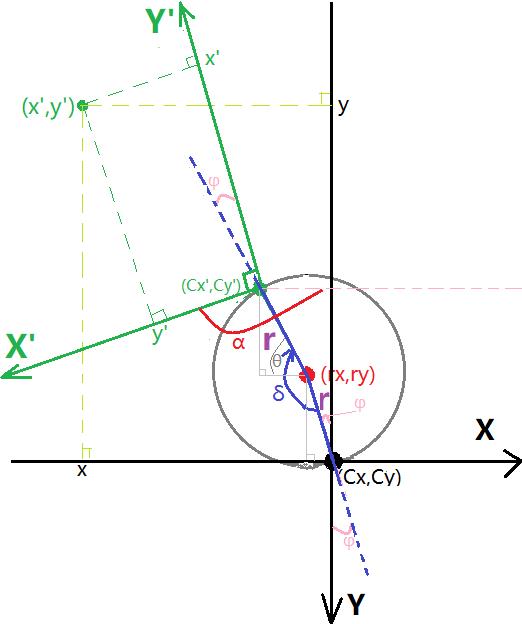
看似更复杂了，其实就是在之前的基础上作了个位移而已：
将以(Cx,Cy)为中心旋转 α 角度后的绿坐标系，平移至现在的旋转中心点(rx,ry)，然后继续沿着半径平移至点(Cx’,Cy’)就形成了上图的坐标位置关系。

之前以(Cx,Cy)为中心旋转的旋转矩阵：
$$\left[\begin{array}{lll}cos\alpha & -sin\alpha & Cx\\ sin\alpha & cos\alpha & Cy\\ 0& 0& 1\end{array}\right]$$
其中，平移分量(dx0,dy0) = (Cx,Cy)
进行两次平移：
1.从(Cx,Cy)平移距离 r 至点(rx,ry)；2.再次平移距离 r 到达以(rx,ry)为中心点旋转的最终位置(Cx’,Cy’)。

第1次平移：(dx1, dy1) = (rx - Cx, ry - Cy)
第2次平移：
φ = atan((Cx - rx) / (Cy - ry))
θ = δ - φ - π / 2
r = √((rx - Cx)² + (ry - Cy)²)
(dx2, dy2) = (-cosθ * r, -sinθ * r)
合总的平移，得到总偏移量：
(dx, dy) = (dx0 + dx1 + dx2, dy0 + dy1 + dy2) = f([Cx,Cy], [rx,ry], δ) 
即：(dx, dy)的值只与画布坐标点(Cx,Cy)、旋转中心点(rx,ry)，以及旋转角度 δ 这3个参数有关。

最后，我们需要计算出 α 角，就是X轴旋转到X'轴的偏移角度，这样才能直接套用之前计算出来的矩阵（保持参数一致性）：
其实，α == φ，因为绕中心点(rx,ry)旋转的角度与X轴偏移角度是一模一样的。不过，下面可以验证一下：
α = π - (π / 2 - φ) + θ，代入 θ 角，即得 α == φ

将以上旋转矩阵的中心点(Cx,Cy)替换刚计算出来的(dx,dy)，即得到绕任意中心点(rx,ry)顺时针(因Y轴向下)旋转任意角度 δ(也即α) 的旋转矩阵：
$$\left[\begin{array}{lll}cos\delta & -sin\delta & f([Cx,Cy],[rx,ry],\delta {)}_x\\ sin\delta & cos\delta & f([Cx,Cy],[rx,ry],\delta {)}_y\\ 0& 0& 1\end{array}\right]$$
最后要说的是，坐标系进行了平移，那么承载这个坐标系的画布的全部元素都进行了平移，所以前面计算逻辑是没有任何问题的，并且整个过程使用的都是随机的一种情况进行计算的，所以最终得出的旋转矩阵没有问题。