图解字符串匹配算法：从Brute-Force到KMP，一下子就整明白了

Posted 2022-09-25 流楚丶格念

文章目录

• Brute-Force算法
• • 算法思想
  • 步骤图解
  • 代码实现
  • 复杂度分析
• KMP算法
• • 算法思想
  • • 部分匹配值产生过程
  • 步骤图解
  • 代码实现

Brute-Force算法

算法思想

Brute-Force算法是一种简单、直观的模式匹配算法。

其实现方式是：
设 s 是主串， t 为模式串； i 为主串当前比较字符的下标；j 为模式串当前比较字符的下标。令 i 的初值为 start，j 的初值为 0 。
从主串的第 start 个字符 ( i = start ) 起和模式串的第一个字符 ( j = 0 )比较,若相等,则继续逐个比较后续字符 ( i++，j++)；

否则从主串的第二个字符起重新和模式串比较( i 返回到原位置加 1， j 返回到 0 )依此类推，直至模式串t中的每一个字符依次和主串 s 的一个连续的字符序列相等，则称匹配成功，函数返回模式串 t 的第一个字符在主串 s 中的位置;否则称匹配失败，函数返回 -1。

步骤图解

主串 s 为“ababcabdabcabca”,模式串 t 为“abcabc”,匹配过程如下：

代码实现

代码如下：

package com.yyl.algorithm.questions;

public class StringMatchDemo 
    public static void main(String[] args) 
        String s = "ababcabdabcabca";
        String t = "abcabc";
        StringMatchDemo bruteforce = new StringMatchDemo();
        int index = getIndex(s, t);
        System.out.println("对应相同字符在原字符串的第" + index + "位开始到" + (index + t.length() - 1) + "位");
    

    public static int getIndex(String s, String t) 
        //主串比模式串长时开始比较
        if (s != null && t != null && t.length() > 0 && s.length() >= t.length()) 
            int sLen = s.length(), tLen = t.length();
            // i j 分别是原字符串 与 目标串下标
            int i = 0, j = 0;
            while ((i < sLen) && (j < tLen)) 
                if (s.charAt(i) == t.charAt(j)) 
                    i++;
                    j++;              //当主串字符与模式串字符相同时，查找成功，主串和模式串同时往后开始遍历匹配
                 else 
                    i = i - j + 1;
                    j = 0;          //主串字符与模式串字符不相同时，查找失败，i 返回到原来位置加 1 ，j 返回到0
                
            
            if (j >= t.length())     // 匹配成功，返回子串的序号
                return i - tLen;
             else                   // 匹配失败，返回-1
                return -1;
            
        
        return -1;
    

运行结果：

复杂度分析

Brute Force模式匹配算法简单且易于理解，但在一些情况下 ,时间效率非常低，其原因是主串 s 和模式串 t 中已有多个字符比较相等时，只要后面遇到一个字符比较不相等，就需将主串的比较位置 i 回退。

假设主串的长度为 n ,子串的长度为 m ,则模式匹配的BF算法在最好情况下的时间复杂度为O(m)，即主串的前 m 个字符刚好等于模式串的 m 个字符。

BF算法在最坏情况下的时间复杂度为O(nm)，分析如下：假设模式串的前 m-1 个字符序列和主串的相应字符序列比较总是相等，而模式串的第 m 个字符和主串的相应字符比较总是不相等，此时，模式串的 m 个字符序列必须和主串的相应字符序列块一共比较 n-m+1次，每次比较 m 个字符，总共需比较m×(n- m+1)次，因此，其时间复杂度为O(nm)。

KMP算法

算法思想

KMP是一个解决模式串在文本串中是否出现过，如果出现过，最早出现的位置的经典算法

KMP算法常用于在一个文本串S中查找一个模式串P的出现位置，这个算法在1977年由Donald Knuth、Vaughan Pratt、James H.Morris三人发表

KMP算法利用之前判断过信息，通过一个next数组，保存模式串中前后最长公共子序列的长度，每次回溯时，通过next数组找到，前面匹配过的位置，省去了大量的计算时间

KMP算法的时间复杂度O(m+n)

部分匹配值产生过程

首先我们要了解字符串的前缀后缀，例如bread这个词

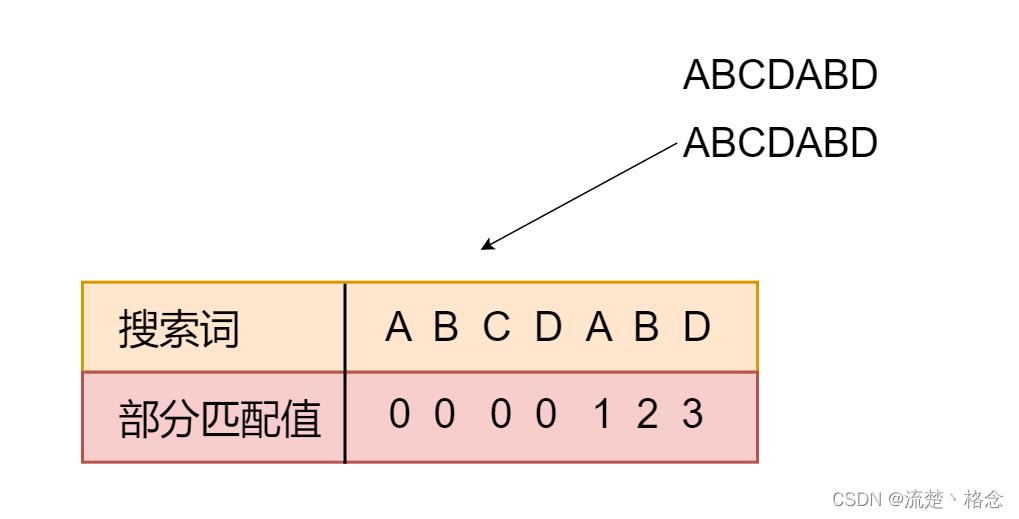
部分匹配值就是前缀和后缀的最长的共有元素的长度，以“ABCDABD为例”

“A”的前缀和后缀都为空集，共有元素的长度为0
“AB”的前缀为A，后缀为B，共有元素为0
“ABC”的前缀为A，AB后缀为BC，C共有元素的长度为0
“ABCDA”的前缀为A，AB,ABC,ABCD，后缀为BCDA,CDA,DA,A共有元素为A，长度为1

我们可以这样理解，对于一个字符的匹配值判断，就看他和前面的第几个字符相等

比如ABCDABD，ABCD的匹配值均为0，但是A与前缀ABCD中的A相同，故匹配值为1，AB与前缀ABCD中的AB相同，故B的匹配值为2，ABD没有与之相同的前缀，故D为0

步骤图解

举个例子：

字符串：str1=“BBC ABCDAB ABCDABCDABDE”，
子串：str2=“ABCDABD”

利用KMP算法判断str1第一次在str2中出现的位置

1.首先，用str1的第一个字符和str2的第一个字符去比较，不符合，关键词向后移动一位

2.重复第一步，还是不符合，再后移

3.一直重复，直到str1有一个字符与str2的第一个字符符合为止

4.接着比较字符串和搜索词的下一个字符，还是符合

5.遇到str1有一个字符与str2对应的字符不符合

6.这时候按照传统算法，我们会继续便利str1的下一个字符，重复第一步，但是这样我们会做很多无用的工作，比如BCD我们已经判断过，已经不用再次进行判断，当空格与D不匹配时，你其实知道前面6个字符是“ABCDAB”。

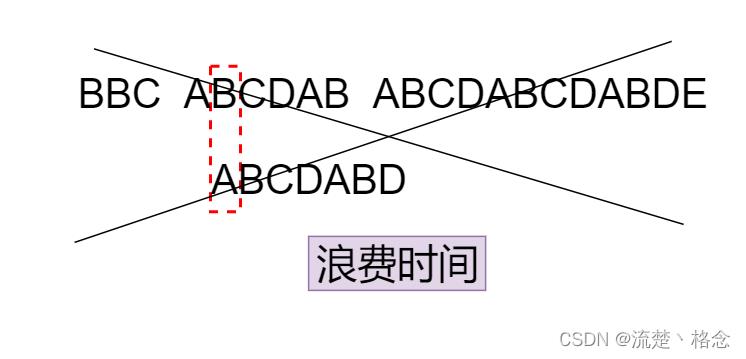
KMP算法的想法是：设法利用这个已知信息，不要把搜索位置移回已经比较过的位置，而是继续将他向后移，这样就提高了效率

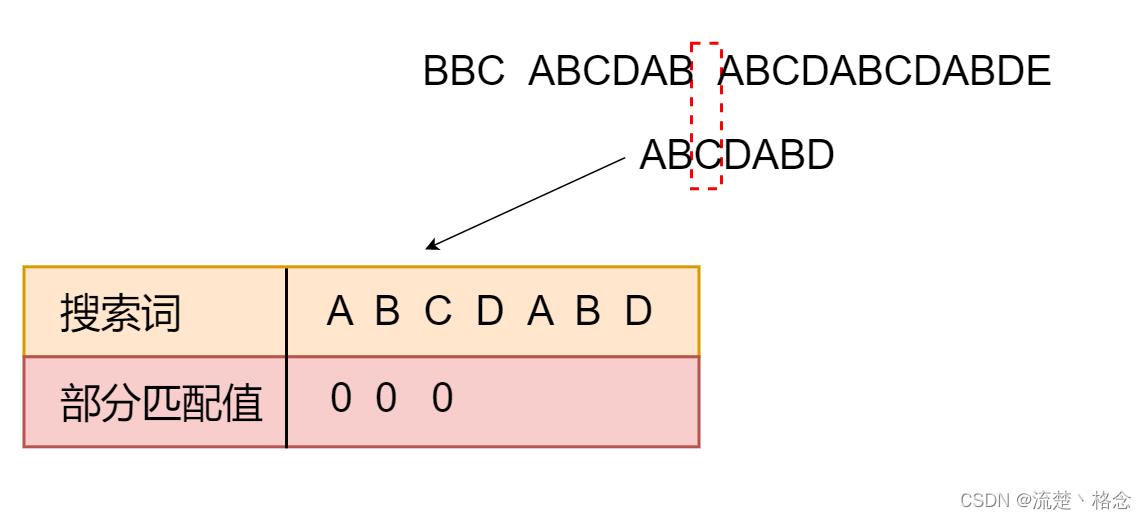
7.我们可以对str2计算出一张部分匹配表如下：

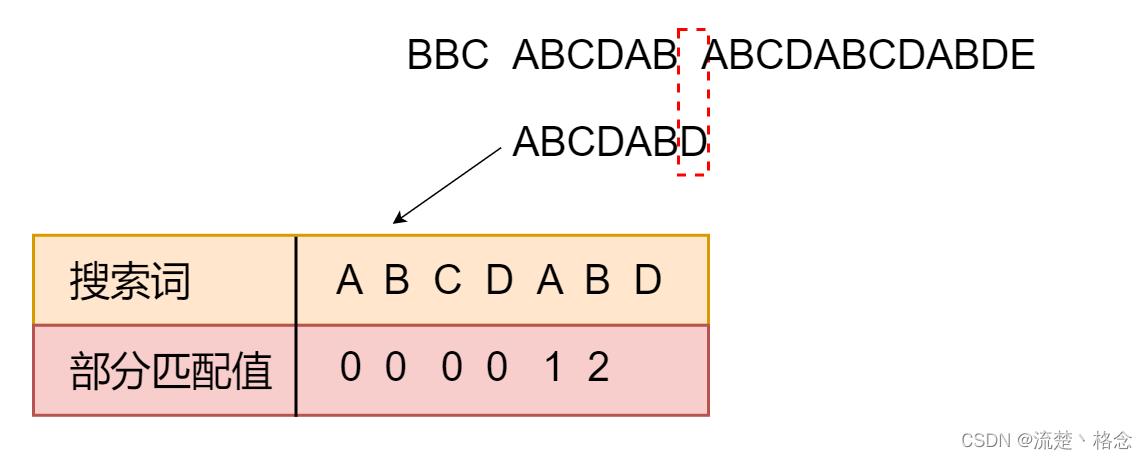
8.已知空格与0不匹配时，前面六个字符“ABCDAB”是匹配的，查表可知，最后一个匹配字符B对应的部分匹配值为2，因此按照下面的公式算出向后移动的位数：

移动位数=已匹配字符数-对应的部分匹配值

因为6-2等于4，所以将搜索词向后移动4位

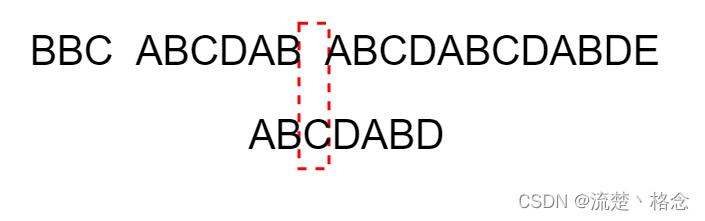
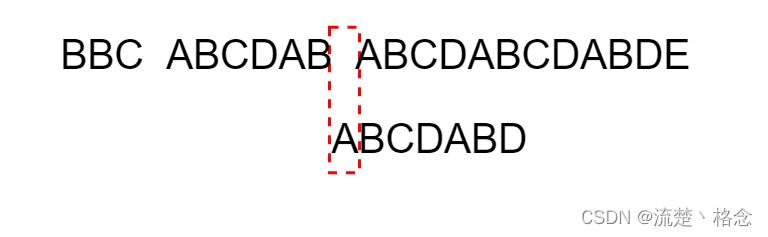
9.因为空格与C不匹配，搜索词继续向后移动，这时，已匹配的字符数为2（“AB”）对应的部分匹配值为0

所以移动为数=2-0，结果为2，于是将搜索词向后移2位

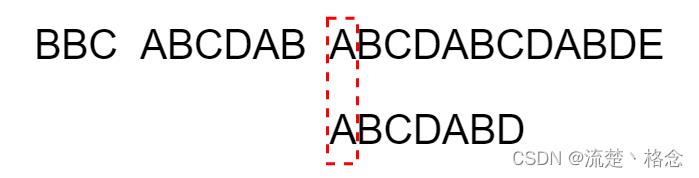
10.因为空格与A不匹配，继续向后移一位

11.逐位比较，直到发现C与D不匹配

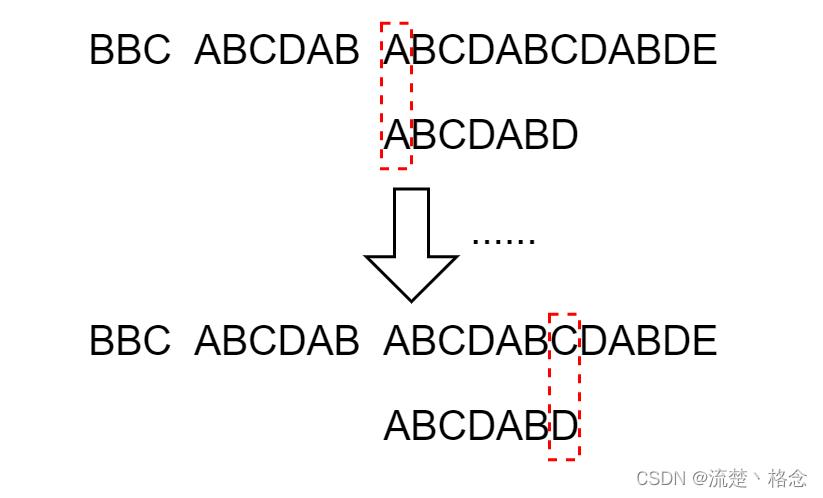
于是，移动为数=6-2，继续向后移动4位

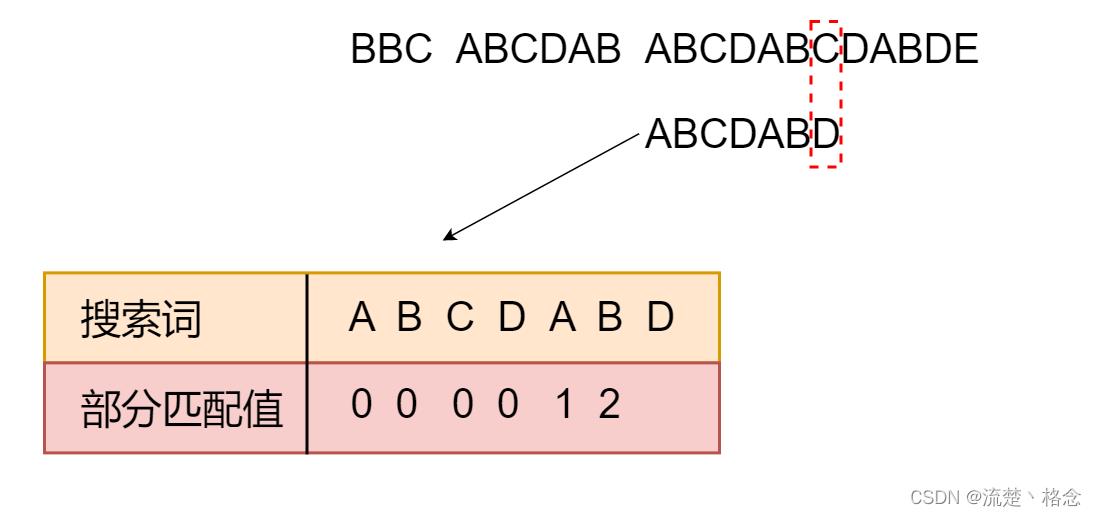
移动完后

12.逐位比较，直到搜索词的最后一位，发现完全匹配，于是搜索完成，如果还要继续搜索（即找出全部匹配），移动位数=7-0，再将搜索词向后移动7位

代码实现

代码如下：

package com.yyl.algorithm.questions;

import java.util.Arrays;

public class StringMatchDemo 
    public static void main(String[] args) 
        String str1 = "BBC ABCDAB ABCDABCDABDE";
        String str2 = "ABCDABD";

        int index2 = strStr(str1, str2);
        System.out.println("KMP算法：对应相同字符在原字符串的第" + index2 + "位开始到" + (index2 + str2.length() - 1) + "位");
    

    /**
     * KMP算法
     *
     * @param source
     * @param target
     * @return
     */
    public static int strStr(String source, String target) 
        if (target.length() == 0) 
            return 0;
        
        // 记录前缀
        int[] next = new int[target.length()];
        getNext(next, target);
        System.out.println(Arrays.toString(next));

        // i 原字符串遍历的下标  j 目标字符串遍历的下标
        for (int i = 0, j = 0; i < source.length(); i++) 
            // 如果不相等就要一直等于前缀
            /*
            因为j表示当前遍历到的目标串的下标，都不一样了，按照常理是j=0直接从头查，但是可能有重复前缀
            那么只能移动到上一个元素的前缀里了就OK了
            
            比到这样的时候
            BBC ABCDAB ABCDABCDABDE
                ABCDABD
                0000122
            不用到下一个再比一下，直接看D的上一个还一样的值的前缀，前缀是2
            BBC ABCDAB ABCDABCDABDE
                    ABCDABD
                    0000122
            那么j再比的时候就直接从 2开始比  也就是比C和空格
            此时 i 就是空格的位置     
            还是在  while (j > 0 && source.charAt(i) != target.charAt(j)) 此时发现还是不同
            j就等于前缀0了  j不大于0了 跳出while，然后i++，再继续比        
             */
            while (j > 0 && source.charAt(i) != target.charAt(j)) 
                j = next[j - 1];
            
            if (source.charAt(i) == target.charAt(j)) 
                j++;
            
            if (j == target.length()) 
                return i - j + 1;
            
        
        return -1;
    

    private static void getNext(int[] next, String target) 
        int len = target.length();
        next[0] = 0;
        //ABCDABD
        for (int i = 1, j = 0; i < len; i++) 
            while (j > 0 && target.charAt(i) != target.charAt(j)) 
                // 如果不同  当前的包含元素的前缀就和前一个一样
                j = next[j - 1];
            
            if (target.charAt(i) == target.charAt(j)) 
                j++;
            
            next[i] = j;
        
    

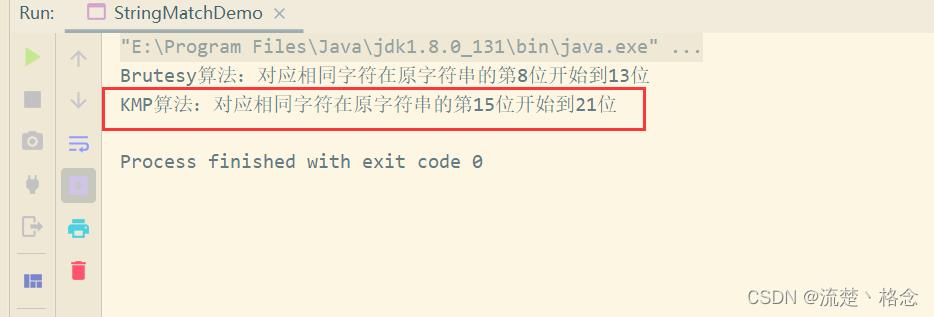
运行结果：