重温基础算法内部排序之桶排序法

Posted 2022-09-24 顧棟

内部排序之桶排序法

桶排序是计数排序的升级版，主要将它利用了函数的映射关系，高效与否的关键就在于这个映射函数的确定。为了使桶排序更加高效，我们需要做到这两点：

1. 在额外空间充足的情况下，尽量增大桶的数量
2. 使用的映射函数能够将输入的 N 个数据均匀的分配到 K 个桶中

同时，对于桶中元素的排序，选择何种比较排序算法对于性能的影响至关重要。

主要思想

1. 准备K个桶，对桶进行编号
2. 遍历待排序系列，将元素放到合理的桶中
3. 对每个桶内的元素进行桶内排序
4. 从第一个桶开始，依次从桶内获取元素，最终形成的序列就是排序完成的序列

过程演示

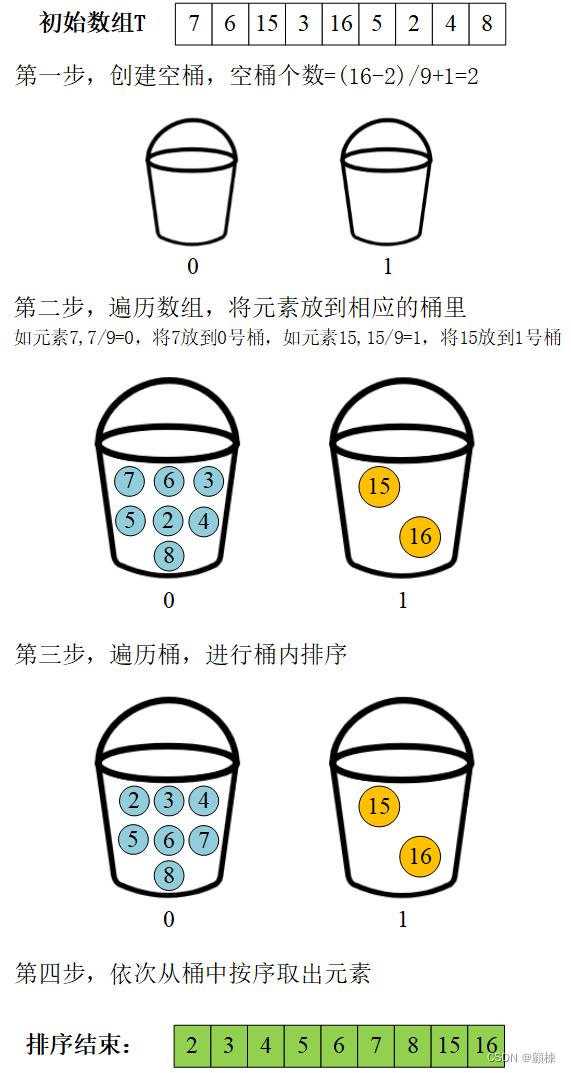
java实现

package sort;

import java.util.Arrays;

public class BucketSort 
    public static void main(String[] args) 
        int[] o = 7, 6, 15, 3, 16, 5, 2, 4, 8;
        System.out.print("排序前: ");
        for (int t : o) 
            System.out.print(t);
            System.out.print(" ");
        
        System.out.println();

        // 算法部分
        // 计算桶的个数，桶的个数多少合适呢？
        int maxValue = o[0];
        int minValue = o[0];
        for (int v : o) 
            if (v < minValue) 
                minValue = v;
             else if (v > maxValue) 
                maxValue = v;
            
        
        // 待排数组中的最大最小差值/单个桶的元素最大个数后再加1
        int bucketCount = (maxValue - minValue) / o.length + 1;
        System.out.println("桶的个数: " + bucketCount);
        int[][] buckets = new int[bucketCount][0];

        for (int j : o) 
            // 计算元素该在哪个桶里/单个桶的元素最大个数
            int index = (j - minValue) / o.length;
            buckets[index] = arrAppend(buckets[index], j);
        

        int arrIndex = 0;
        // 依次遍历桶
        int count = 1;
        for (int[] bucket : buckets) 
            // 排除空桶
            if (bucket.length <= 0) 
                continue;
            
            // 对每个桶进行排序，这里使用了插入排序
            insertSort(bucket);
            System.out.print("第" + count + "个桶排序后: ");
            for (int value : bucket) 
                o[arrIndex++] = value;
                System.out.print(value);
                System.out.print(" ");
            
            System.out.println();
            count++;
        

        System.out.print("排序后: ");
        for (int t : o) 
            System.out.print(t);
            System.out.print(" ");
        
        System.out.println();

    

    /**
     * 扩容数组
     */
    private static int[] arrAppend(int[] arr, int value) 
        arr = Arrays.copyOf(arr, arr.length + 1);
        arr[arr.length - 1] = value;
        return arr;
    

    private static void insertSort(int[] o) 
        for (int i = 1; i < o.length; i++) 
            int temp = o[i];
            for (int j = i; j > 0; j--) 
                if (temp < o[j - 1]) 
                    o[j] = o[j - 1];
                    o[j - 1] = temp;
                 else 
                    break;
                
            
        
    

结果

排序前: 7 6 15 3 16 5 2 4 8 
桶的个数: 2
第1个桶排序后: 2 3 4 5 6 7 8 
第2个桶排序后: 15 16 
排序后: 2 3 4 5 6 7 8 15 16 

算法分析

时间复杂度

与桶的内部采用的排序算法有关

若有$n$个元素，$m$个桶，桶内采用的是快速排序。那么平均情况下每个桶内的元素个数就是$k=\frac{n}{m}$，其时间复杂度就是$klo{g}_2^k$。$m$个桶，当$m$无限接近$n$时，其复杂度就是$O(n)$，当$m=1$时，复杂度就是$O(nlo{g}_2^n)$。

空间复杂度

与桶的内部采用的排序算法有关

若有$n$个元素，$m$个桶，桶内采用的是快速排序。那么平均情况下每个桶内的元素个数就是$k=\frac{n}{m}$，桶内排序需要$lo{g}_2^k$个空间。$m$个桶，当$m$无限接近$n$时，其复杂度就是$O(n)$，当$m=1$时，复杂度就是$O(lo{g}_2^n)$。