IEEE754标准以及非常规划定义，double的二进制转换工具类

Posted 2022-09-21 黑马程序员官方

IEEE754标准

​ 今天我们要讨论的问题是在Java中：double pi = 3.14; 在内存中第10位上是0还是1？

​ 这个问题需要我们了解Java中double类型在内存中是如何存储的。那么你知道Java是如何存储double类型变量的吗？有小伙伴说“内存中当然是存二进制了！”没错，但具体是如何存储了呢？

​ 今天我们就来聊一聊Java中浮点数存储的标准，它叫IEEE754。当你看完本篇文章后，你就可以知道3.14在内存中每一位上是0还是1了。茶语饭后与同行们闲谈时，相信十人中有九人不知道啥是IEEE754，那么让我们开始吧。

我们分为如下三步骤来学习，分别是：

1、 数学中的小数十进制与二进制的转换方法

2、 小数的科学记数法格式

3、 IEEE754标准

一、数学中的小数十进制与二进制的转换方法

1.1 十进制小数转换为二进制

​ 如果你已经对小数的进制转换很熟悉了，那么可以跳过本节，直接看科学记数法格式小节。

​ 我们以(121.375)₁₀为例，把它转换成二进制。

​ 首先我们把它拆分成整数与小数两个部分，因为整数与小数的转换方式是不同的。我们先来看整数部分的转换公式。

• 整数部分转换为二进制：除以2，倒序取余

• 小数部分转换为二进制：乘以2，正序取整

所以十进制小数121.375转换为二进制为：1111001.011

小伙伴们要注意了，这只是数学层面上的转换，并不是Java内存中保存的样子。想要了解Java内存中double类型的样子必须学习IEEE754才能知道。

1.2 二进制转换为十进制

• 整数部分转十进制：按权展开求和

  例如：

  假如二进制为：0000 0001，结果就可以表示为：1 * 2º = 1
  
  假如二进制为：0000 0010，结果就可以表示为：1 * 2¹ = 2
  
  假如二进制为：0000 0100，结果就可以表示为：1 * 2² = 4
  
  所以，如果二进制为：0000 0111，结果就可以表示为：
  
     1 * 2² + 1 * 2¹ + 1 * 2º  
  
   = 4 + 2 + 1
  
   = 7
  

  针对此例，整数部分二进制：1111001，就可以表示为：

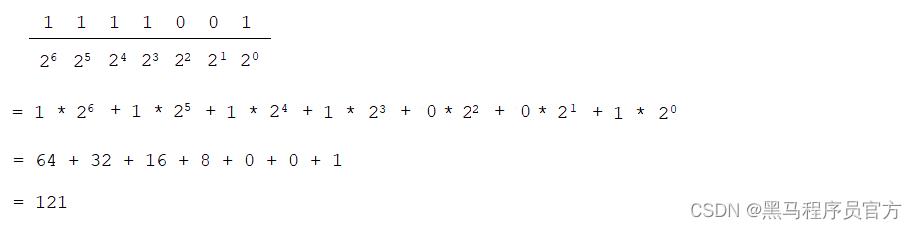
• 小数部分转十进制：按权展开求和

  针对此例，小数部分二进制：0.011，就可以表示为：

二、科学记数法

2.1 什么是科学计数法

​ 科学记数法是一种记数的方法。把一个十进制数表示成a与10的n次幂相乘的形式（1≤|a|<10，a不为分数形式，n为整数），这种记数法叫做科学记数法。

​ 例如：数字：98024.25，用科学计数法可以表示为：9.802425 * 10⁴，也可以表示为：9.802425E4

​ 数字：0.00325，用科学计数法可以表示为：3.25 * 10^-3，也可以表示为：3.25E-3

其中：

1. 其中9.8024和3.25就是a：它一定是1 ≤ |a| < 10的，也就是：a的绝对值要大于等于1，并且小于10.所以它一定是一个一位数，不能是两位数。

2. 10为底数：因为是十进制的科学计数法，所以这里是10.

3. 4和-3为指数n：它一定是个整数。

​ 使用科学计数法记数的一个好处是：在表示一个较大的数，或者较小的数时，可以节省空间和时间。

三、IEEE754标准

​ 我们已经了解了二进制与十进制之间的转换，以及小数的科学记数法。现在我们学习一下IEEE754规范中小数在是如何在内存中存储的。

3.1 64位划分成三个区

​ 通过上面的学习相信你已经了解了科学记数法了。那么IEEE754标准是怎样的呢？我们已经知道double类型是8个字节，也就是64位。其实IEEE754标准把这64位分成了三个区域，分别对应科学记数法的符号、底数、指数。只不过略有一些特殊性而已，下面我们来看一张图。

这个64位的二进制表示的浮点数到底是多少呢？我们本节都会使用这个例子来做演示。

下面先来看一个公式，然后我们通过这个公式展开讲解。

​ 浮点数＝s(±1) ×(1.f)₂ ×2^e-1023

​ 现在你可能还不能理解这个公式，不急，我们先来看二进制图。

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-YmGtguPL-1663670616951)(T1-IEEE754标准/1655143937684.png)]

​ 图中说明第一个区域是符号区，只有一位就是第63位。为0表示正；为1表示负。这个很好理解。上例中符号区为0，所以可以理解为s=1；当符号区为1时，可以理解为s=-1。

第二个区域是阶码区，范围是第52位到第62位，共有11位。阶码区与指数有关。

最后一个区域是尾数区，范围是第0位到第61位，共有52位。尾数区与底数有关。

我们大致了解了一下double的64位分的三个区，下面我们详细来聊一聊阶码区与尾数区。

3.1.1 符号区

符号区很好理解，它只占一位（最后一位）。通常我们用字母S来表示，如果为0表示正数，那么就是s=1；如果为1表示负数，那么就是s=-1。

3.1.2 阶码区

​ 阶码区中11位二进制范围是00000000000 ~ 11111111111，对应的十进制范围是0 ~ 4096。但它并不能表示最小指数是0最大指数是4096。因为还要表示负的指数，所以IEEE754规定阶码区的值减去1023才是最终的指数。

指数*=阶码区-1023*

当阶码区的值为1000时，再减去1023，那么最终指数就是-23了。通过这种方式就可以有负的指数了。

例如阶码区为10000000101时，那么指数等于什么呢？我们先把它转换成十进制为1029，再减去1023，结果为1029-1023=6。

s(±1)×1.f×2⁶

3.1.3 尾数区

​ 我们已经了解了符号区与阶码区，下面我们聊一聊尾数区。尾数区共52位，从第0位到第51位。我们需要在这52位的尾数前面添加“1.”就是底数了。例如尾数区为

1110010110000000000000000000000000000000000000000000，

那么底数就是：**1.**1110010110000000000000000000000000000000000000000000

IEEE754隐藏了“1.”，一定要记住这一特性，不然会计算出错的。

现在尾数区与底数之间的关系已经明白了，那么计算起来也就不难了。我们把上面二进制底数中无用的零去除：1.111001011。

让这个数乘以×2⁶，也就是(1.111001011)₂×(2⁶)₁₀，等同于把小数点向右移动6位。即：(1.111001011)₂×(2⁶)₁₀ = (1111001.011)₂

转换成十进制后的结果为：121.375

四、IEEE754中非常规化定义

​ 上面已经了解了IEEE754中规范化的定义，但IEEE754中还存在一些非规范的定义，以及本节中还要讨论为什么double类型的范围是±1.79×10³⁰⁸；double类型的非零最小绝对值是多少？为什么？

4.1 表示"零"(非常规)

​ 在I浮点数中不能精确的表示0，只能以很小的数近似的表示0。所以IEEE754标准表示0时，直接将阶码与尾数全部设置为0。IEEE754中，可以表示“+0"和"-0"：

1、零（非常规）：当阶码与尾数都是全0时，表示0。符号为0表示正0；符号为1表示负0
   0 00000000000 0000000000000000000000000000000000000000000000000000

4.2 表示"无穷"(非常规)

​ 根据IEEE754标准，当要存储的数大于规格数取值范围的最大值时, 就会被记做+infinity，当要存储的数小于规格数取值范围的最小值时, 就会被记做-infinity。

​ 例如，对于以下代码：

double d1 = 1.8 * Math.pow(10, 308);//超出double的存储范围
double d2 = -1.8 * Math.pow(10, 308);//超出double的存储范围
System.out.println(d1);//Infinity
System.out.println(d2);//-Infinity

​ 再例如，以下代码：

System.out.println(10.0 / 0);//Infinity

​ IEEE754中，无穷(Infinity)被表示为：

2、无穷（非常规）：当阶码区为11个1，并且尾数52个0时，表示无穷。符号为0表示正无穷；符号为1表示负无穷
   0 11111111111 0000000000000000000000000000000000000000000000000000

4.3 表示"NaN"(非常规)：

​ 在IEEE754中，如果计算出来的不是一个数值，则结果为：NaN

​ 例如，对于以下代码：

System.out.println(0.0 / 0);//NaN

​ 在IEEE754中，NaN被表示为：

3、NaN（非常规）：当阶码区为11个1，并且尾数为是0时，表示NaN(非数字)。
   0 11111111111 1000000000000000000000000000000000000000000000000000

​ 注意：NaN没有+NaN或-NaN的说法，全部被统称为：NaN

4.4 表示"最大值"（常规化）

​ double的最大值为：1.79E308，IEEE754标准中，最大值存储方式为：

4、最大值（常规化）：当阶码区为11111111110，并且尾数区是52个1时，表示最大值。1.79E308
    0 11111111110 1111111111111111111111111111111111111111111111111111
    * 指数：11111111110转换为十进制为2046，减去1023等于1023
    * 底数：1.1111111111111111111111111111111111111111111111111111
    * 运算：等于pow(2, 1024)-1，但如果使用Math.pow(2, 1024)会出现无穷大。可以计算       
           Math.pow(2,1023.9999)

4.5最小绝对值（非常规）

5、最小绝对值（非常规）：当阶码为11个零时，并且尾数区是51个0 + 1个1时，表示正数的最小值。4.9E-324
    * 0 00000000000 0000000000000000000000000000000000000000000000000001
    * 当指数为0，并且尾数不为0时，尾数隐藏固定值不再是“1.”，而是“0.”，同时指数偏移量不再是1023，而是1022
    * 指数：00000000000转换为十进制0，减去1022等于-1022。
      > 0.0000000000000000000000000000000000000000000000000001
      > 上面的数值1在小数点后第52位，再把小数点左移1022个位，即1074
      > pow(2, -1074)的结果是4.9E-324

五、double的二进制转换工具类

​ 将一个double的十进制小数转换为IEEE754标准的二进制表示比较困难，所以我在下面为大家提供了一个工具类，可以很好的完成这个工作。

public class IEEE754 
    public static void main(String[] args) 
        DoubleBinary db = new DoubleBinary(3.14);
        System.out.println(db);
    
	

class DoubleBinary 
    private Double d;//数值本身
    private String binary;//double类型转换后的完整二进制字符串
    private String sign;//二进制字符串的符号位(表示有无符号)
    private String exponent;//指数段(exponent-1023等于指数)
    private String fraction;//底数段(在fraction前面添加“1.”就是底数)

    // 使用double变量构造本类对象
    public DoubleBinary(double d) 
        this.d = d;
        this.init();
    

    // 使用二进制字符串构造本类对象
    public DoubleBinary(String binary) 
        this.binary = binary;
        this.init();
    

    /*
    初始化方法，构造器都会调用本方法
     */
    private void init() 
        if(binary == null) // 如果binary为null，说明当前使用的是doubel的构造器
            binary = doubleToBinary(d);//把double对象转换成二进制字符串，赋给binary
         else // 如果binary不为null，说明当前使用的是String的构造器
            this.d = binaryToDouble(binary);//把binary转换成double变量，赋给d
        
        // 分解binary到三个区中
        this.sign = binary.substring(0, 1);
        this.exponent = binary.substring(1, 12);
        this.fraction = binary.substring(12);
    

    public String getSign() 
        return this.sign;
    

    public String getExponent() 
        return this.exponent;
    

    public String getFraction() 
        return this.fraction;
    

    public String getBinary() 
        return binary;
    

    public double getDouble() 
        return this.d;
    

    // 格式化输出，在三个区中间添加“-”
    public String toString() 
        return sign + "-" + exponent + "-" + fraction;
    

    // 将二进制字符串转换成double类型
    public static double binaryToDouble(String binary) 
        long l = Long.valueOf(binary, 2);// 把字符串转换成long类型
        return Double.longBitsToDouble(l);// 把long类型的二进制转换成double变量
    

    // 将double类型转换成二进制字符串
    public static String doubleToBinary(double d) 
        return longToBinary(Double.doubleToLongBits(d));// 先把double转换成long类型，再把long类型转换成二进制字符串
    

    // 将long型转换成二进制字符串
    // Long类中提供了把long类型转换成二进制字符串的方法，但会去除前导0，所以没有使用
    public static String longToBinary(long l) 
        long x = 1L;//创建63个0 + 1个1的变量，用来与指定long类型变量进行“&”运算
        StringBuilder sb = new StringBuilder();//用来装载二进制字符串
        /*
        循环64次，每次让指定long型变量与x进行按位与运算。然后再把x左移一位
        运算结果不等于0，说明当前位的值是1，否则为0
         */
        for(int i = 0; i < 64; i++) 
            long xx = l & x;//让参数l与x进行&运算，当x的1在哪一位上，哪一位的值就会保留下来，其他位清零
            if(xx != 0) sb.insert(0, 1);//如果当前位是1，那么结果就不会等于零
            else sb.insert(0, 0);//如果当前位是0，说明所有位都是0，那么结果就是0
            x <<= 1;//移动1的位置，对下一位进行判断
        
        return sb.toString();
    

5.1 代码说明

​ 上面的代码可以将一个double值(例如：3.14)，转换为二进制"符号位-阶码区-尾数区"的字符串表示(例如：0-10000000000-1001000111101011100001010001111010111000010100011111)。接下来我们对主要的工具类：DoubleBinary类做个简要说明：

• 这个类的五个成员属性：

  • Double d：存储要转换的double值。这个值通过构造方法初始化。
  • String binary：存储转换后的完整的二进制字符串。
  • String sign：存储转换后的二进制字符串中："符号位"部分。
  • String exponent：存储转换后的二进制字符串中："阶码"部分。
  • String fraction：存储转换后的二进制字符串中："尾数"部分。

• 两个构造方法：

  • public DoubleBinary(double d)：double参数的构造方法。参数用于初始化成员属性：d

  • public DoubleBinary(String s)：String参数的构造方法。用于接收一个String表示的二进制，例如：“0100000000001001000111101011100001010001111010111000010100011111”。参数用于初始化成员属性：binary。

    这两个构造方法保证了对于两个成员属性d和binary初始化其中一个。

• 在两个构造方法中，进行初始化后，都调用了init()方法：

  • 在init()方法中首先判断了对成员属性binary进行了初始化，还是对成员属性d进行了初始化：

    • 代码：if(binary == null)说明对成员属性d进行了初始化，这时调用本类的另一个方法doubleToBinary(d)将double值转换为二进制。
    • 代码：else说明对成员属性binary进行了初始化，这时调用本类的另一个方法binaryToDouble(binary)将字符串转换为double值。

  • 这个if判断后，保证了两个成员属性d和binary全部被初始化。

  • 后面对binary字符串进行截取，分别取出：符号位、阶码区、尾数区，并初始化三个成员属性：

    ​ this.sign = binary.substring(0, 1);
    ​ this.exponent = binary.substring(1, 12);
    ​ this.fraction = binary.substring(12);

• public static String doubleToBinary(double d)方法：用于将一个double值转换为String表示的二进制。这里的转换思路是：

  • 代码：Double.doubleToLongBits(d)：将这个double值的二进制转换为一个long整数值。

  • 代码：longToBinary(…)：再获取这个long整数值的二进制表示。

  • 方法：longToBinary()：在Java类库的Long类中提供了把long类型转换成二进制字符串的方法，但会去除前导0，所以没有使用，所以这里我们自己定义了一个方法，将一个long值的每一位准确的取出。这个方法的具体工作流程是：

    • 接收一个long类型值，例如：3598，

    • 然后定义一个long类型的变量：long x = 1L;它的二进制是：(0000…1)

    • 接着定义一个StringBuilder，用于封装结果。

    • 然后一个64次的循环，用x和参数3598的每位进行&运算，取出每一位的值。&运算是：两位都为1结果为1，否则为0。

      例如：

      第一次循环：

    ​ 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0001

    & 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 1110 0000 1110

    ---

    ​ 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000(结果:0)

    ​ 然后：x << 1，左移1位，进行第二次循环：

    ​ 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0010

    & 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 1110 0000 1110

    ---

    ​ 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0010(结果:!=0)

    ​ …

    • 代码：if(xx != 0)也就是"结果!=0"说明二进制位为1，所以向StringBuilder中插入：1，否则，向StirngBuilder中插入：0，最后StringBuilder中就是这个long值的二进制表示。

• 我们再看public static double binaryToDouble(String binary)方法：用于将一个String的二进制转换为double值。

  • 这个方法中首先long l = Long.valueOf(binary, 2);是将二进制转换为一个long值。
  • 代码：return Double.longBitsToDouble(l);将这个long值的二进制转换为double值。

  这个方法在本例中并不是主要的方法，为了此工具类的完整性所以提供了此方法，转换后的double值可以通过本类的getDouble()来获取。

六、结束语

​ 到这里我们就把IEEE754标准的基本内容都讲完了，希望大家能对IEEE754标准有一个深入的了解，在将来的面试以及编码中，更能够对double的底层存储机制进行更深入的理解和熟练的掌握。

​

我们再看public static double binaryToDouble(String binary)方法：用于将一个String的二进制转换为double值。

• 这个方法中首先long l = Long.valueOf(binary, 2);是将二进制转换为一个long值。
• 代码：return Double.longBitsToDouble(l);将这个long值的二进制转换为double值。

这个方法在本例中并不是主要的方法，为了此工具类的完整性所以提供了此方法，转换后的double值可以通过本类的getDouble()来获取。

六、结束语

​ 到这里我们就把IEEE754标准的基本内容都讲完了，希望大家能对IEEE754标准有一个深入的了解，在将来的面试以及编码中，更能够对double的底层存储机制进行更深入的理解和熟练的掌握。

​