依据象限搜索及混合预计耗费的A*改进算法，包含8邻域及24邻域的改进

Posted 2022-09-20 slandarer

注： 以下改进皆为在传统 A* 算法基础下的改进，请先了解传统 A* 算法后再对本文进行了解。

1 邻域改进

当终点相对于当前点在不同象限时，采取不同的搜索邻域能够减小检验节点数量。

首先要确定终点相对于当前节点象限，我们定义向量：
$$V=[\frac{goal.x-cur.x}{2}，\frac{goal.y-cur.y}{2}]$$
其中$goal$为目标结点，$cur$为当前节点，则：
$$\{\begin{array}{ll}V(1)\ge 0,V(2)\ge 0& 第一象限\\ V(1)\le 0,V(2)\ge 0& 第二象限\\ V(1)\le 0,V(2)\le 0& 第三象限\\ V(1)\ge 0,V(2)\le 0& 第四象限\end{array}$$

依据象限不同我们对搜索邻域做如下改进

1.1 [8]邻域改进

对于不同象限，将传统的8邻域改为5邻域：
如图所示黑色方块代表当前点，蓝色方块表示依据象限搜索的邻域：

1.2 [24]邻域改进

对于不同象限，将24邻域改为13邻域：
如图所示黑色方块代表当前点，蓝色方块表示依据象限搜索的邻域：

2 混合预计耗费估计

2.1 欧几里德距离

当前节点与目标点间无障碍时
采取欧几里德距离x10作为预计耗费 ：
$$H=10\ast \sqrt{(g_x-c_x{)}^2+(g_y-c_y{)}^2}$$

2.2 半圆周距离

如图所示，当起点终点连线穿过障碍物，但至少有一个以当前点和终点的中点为圆心的半圆弧能够无障碍的连接当前点和终点，则采用圆弧长度x10作为预计耗费:

若$\overline{AC}=2R$，则$H=10\pi R$

2.3 弧+半径距离

若起点终点间有障碍，且过以中心点为圆心得圆弧两侧都有障碍，则考虑以终点为圆心，当前点及终点距离为半径做圆，若存在圆弧可连接当前点及终点，则考虑(圆弧+半径距离)x10为预计耗费：

若$\overline{AC}=2R$，则$H=10(2\theta R+2R)$

2.4 曼哈顿距离

在以上任意一种类型路径上均存在障碍物，则采用曼哈顿距离：
$$H=10\ast (|g_x-c_x|+|g_y-c_y|)$$

3 结果展示

3.1 [5]邻域及[13]邻域效果

5邻域：

13邻域：

3.2 [13]邻域与传统A*对比一

可以看出改进后的算法搜索范围对比传统方法小了很多
13邻域(左)，传统8邻域(右)

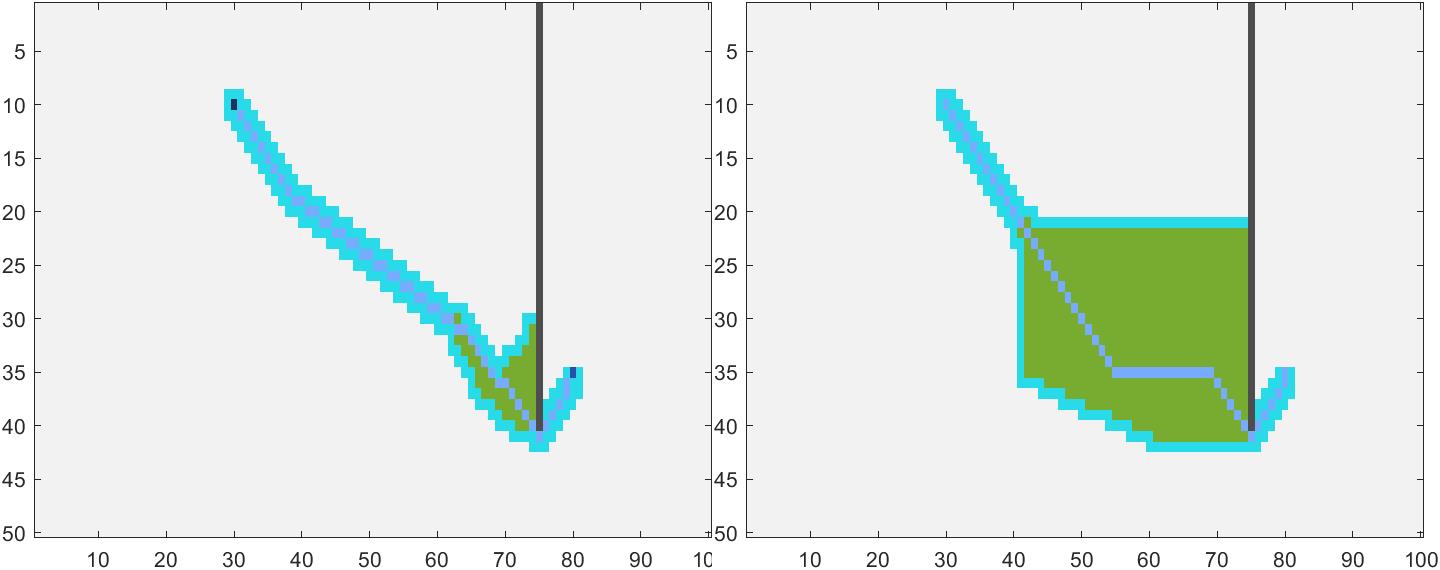
3.2 [13]邻域与传统A*对比二

13邻域(左)，传统8邻域(右)

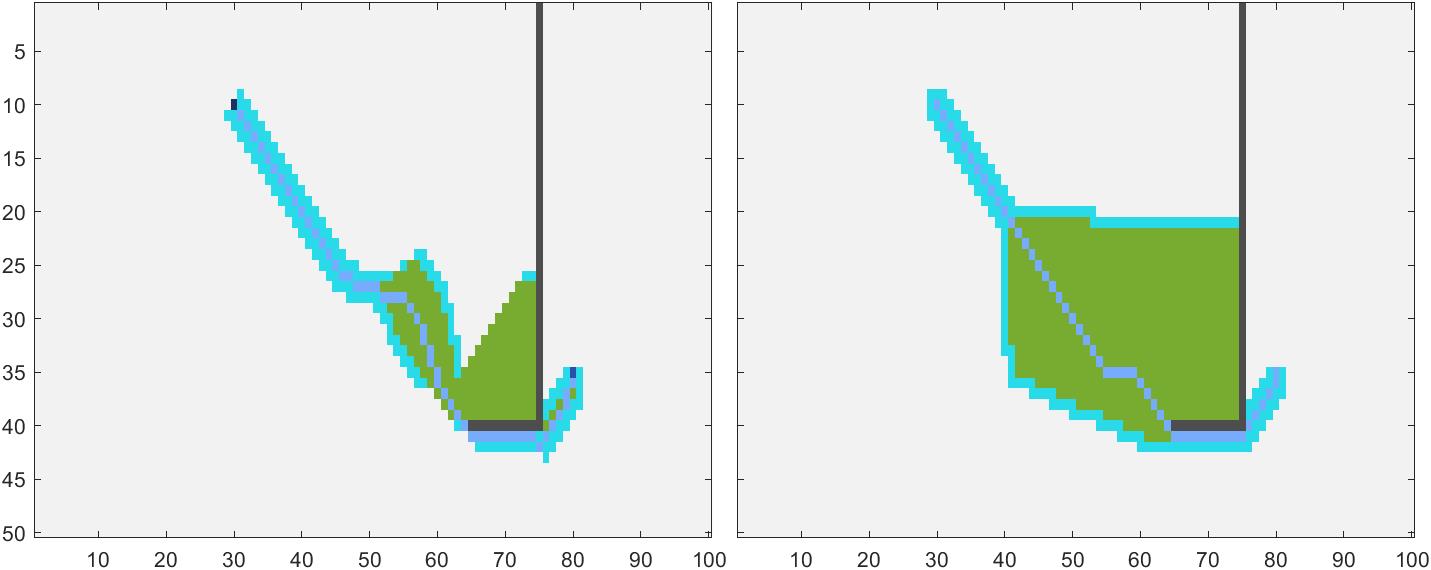
4 主要部分代码

4.1 预计耗费部分代码

function H=getH(pnt1,pnt2,obstacle)
%pnt1,pnt2,obstacle


% =========================================================================
% 情况一，起始点和终点之间无障碍物
flag1=false;

% 先删除明显离直线过远或者垂直点不在起点终点之间的点
tempSet=obstacle;
tempSet(tempSet(:,1)<min(pnt1(1),pnt2(1)),:)=[];
tempSet(tempSet(:,1)>max(pnt1(1),pnt2(1)),:)=[];
tempSet(tempSet(:,2)<min(pnt1(2),pnt2(2)),:)=[];
tempSet(tempSet(:,2)>max(pnt1(2),pnt2(2)),:)=[];

% 找到垂直于起始终止点之间单位向量
tempV=pnt2-pnt1;
tempV=[tempV(2),-tempV(1)]./norm(tempV);

% 障碍点到直线距离
dis_L=(tempSet-pnt1)*tempV';
tempSet(abs(dis_L)>sqrt(2)/2,:)=[];
dis_L(abs(dis_L)>sqrt(2)/2)=[];

if any(abs(dis_L)<0.5) % 如果有距离小于0.5的点，则一定挡住路径
    flag1=true;
else % 如果没有距离小于0.5则检测是否过经过角点    
    extend1=(tempSet+[.5,.5]-pnt1)*tempV';
    extend2=(tempSet+[-.5,.5]-pnt1)*tempV';
    extend3=(tempSet+[.5,-.5]-pnt1)*tempV';
    extend4=(tempSet+[-.5,-.5]-pnt1)*tempV';
    extend=[extend1,extend2,extend3,extend4];
    extend=abs(extend)<=1e-10;
    if any(sum(extend,2)<1)
        flag1=true;
    end
end

if ~flag1
    H=sqrt((pnt1-pnt2)*(pnt1-pnt2)')*10;
    return
end


% =========================================================================
% 情况二，起始点和终点之间有障碍物，弧ABC无阻挡
flag2=false;

R1=sqrt((pnt1-pnt2)*(pnt1-pnt2)')/2; % 圆半径
O1=(pnt1+pnt2)./2;                   % 圆中心

% 找到在圆周上的障碍物
dis_O1=sqrt(sum((obstacle-O1).^2,2));
bool_O1=(dis_O1<(R1+1/2))&(dis_O1>(R1-1/2));
tempSet=obstacle(bool_O1,:);

% dis_L1为点到起点终点连线距离
% dis_L1有正有负才说明两个圆弧都被堵
dis_L1=(tempSet-pnt1)*tempV';
if any(dis_L1>0)&&any(dis_L1<0)
    flag2=true;
end

if ~flag2
    H=pi*R1*10;
    return
end


% =========================================================================
% 情况三，起始点和终点之间有障碍物，弧ABC有遮挡，弧AD无遮挡
flag3=false;
R2=sqrt((pnt1-pnt2)*(pnt1-pnt2)'); % 圆半径

% 找到在圆周上的障碍物
dis_O2=sqrt(sum((obstacle-pnt2).^2,2));
bool_O2=(dis_O2<(R2+1/2))&(dis_O2>(R2-1/2));
tempSet=obstacle
以上是关于依据象限搜索及混合预计耗费的A*改进算法，包含8邻域及24邻域的改进的主要内容，如果未能解决你的问题，请参考以下文章
 
 四叉树平面分割算法--快速图元搜索
 matlab改进大规模邻域搜索算法求解路径优化
 matlab改进大规模邻域搜索算法求解路径优化
 matlab改进大规模邻域搜索算法求解路径优化
 基于Tent映射改进的混合灰狼算法matlab代码
 单目标优化求解基于matlab混合正弦余弦算法和Lévy飞行改进麻雀算法求解单目标优化问题含Matlab源码 1653期