计算机图形学-纹理映射计算重心坐标UV插值双线性插值MipMap

Posted 2022-09-20 点燃火柴

纹理映射

• 1 纹理映射
• • 1.1 什么是纹理映射
  • 1.2 纹理的UV坐标
  • 1.3 读取纹理
• 2 重心坐标
• • 2.1 计算重心坐标
  • 2.2 使用重心坐标做插值运算
• 3 纹理映射常见问题
• • 3.1 纹理太小
  • • 3.1.1 产生原因
    • 3.1.2 解决办法
  • 3.2 纹理太大
  • • 3.2.1 纹理太大的影响
    • 3.2.2 走样产生原因
    • 3.2.3 解决办法
    • • 3.2.3.1 超采样（MSAA）
      • 3.2.3.2 MipMap
      • 3.2.3.3 MipMap的限制

1 纹理映射

1.1 什么是纹理映射

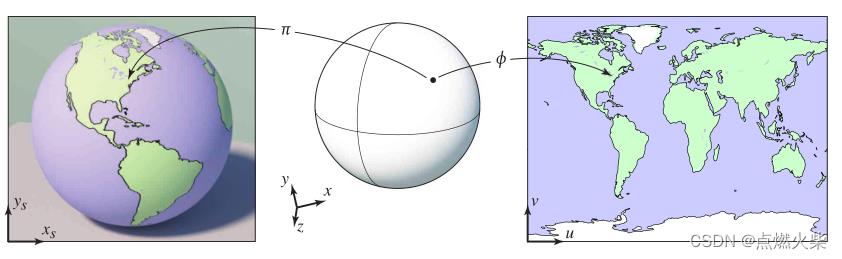
如上图球的表面贴上一张绘制了地图的二维图片，就变成了地球仪，这张二维的图片就是纹理，
把这个图贴到球表面伴随着这纹理的放大缩小以及将纹理中的某个点和球上的某个点对应起来，这个过程就是纹理映射

纹理映射的过程通常是这样的，建模人员给开发人员的模型中通常会有与顶点一一对应的uv坐标，同时提供一张纹理贴图，比如说要对模型的某个顶点着色，这时获取到这个顶点对应的uv坐标，拿着这个坐标从纹理贴图中取色，取到后把值赋给存储顶点颜色的变量

1.2 纹理的UV坐标

如上图左侧是个白模，右侧是使用贴图后的效果，如何准确找到纹理与模型的贴合点，这个就需要用到UV坐标，一张纹理通常会有自己的纹理坐标，如下图，纹理坐标系以左下角为原点，向右为u正方向，向上为v正方向，不论贴图时正方向还是长方形，u和v的取值范围都是[0,1]

1.3 读取纹理

上文中提到着色时，可以获取到每一个顶点对应的纹理坐标，然后从纹理中取色，这样只是为了说明使用纹理的过程，例如处理一个三角形的纹理映射，我只知道三个顶点的坐标和纹理坐标，如何计算三角形内任意一点的纹理坐标呢，答案是做插值，做插值时需要用到重心坐标

2 重心坐标

三角形ABC，该三角形所在平面内任意一点(x,y)可以用该三角形三个顶点坐标的线性组合表示，此时(α，β，γ )所表示的点就是该点的中心坐标
例如三个顶点的中心坐标分别是 A：(1,0,0) 、B：(0,1,0)、C：(0,0,1)
注意：
1.α+β+γ = 1 是将所求的点限定在三角形所在的平面内
2. α、β、γ 的取值必须都大于0，满足都大于0可以将所求的点限定在三角形内

2.1 计算重心坐标

通过面积计算
如下图α的值为A点对面的三角形AA除以三角形总面积；β的值为B点对面的三角形BB除以三角形总面积；γ 的值为C点对面的三角形CC除以三角形总面积

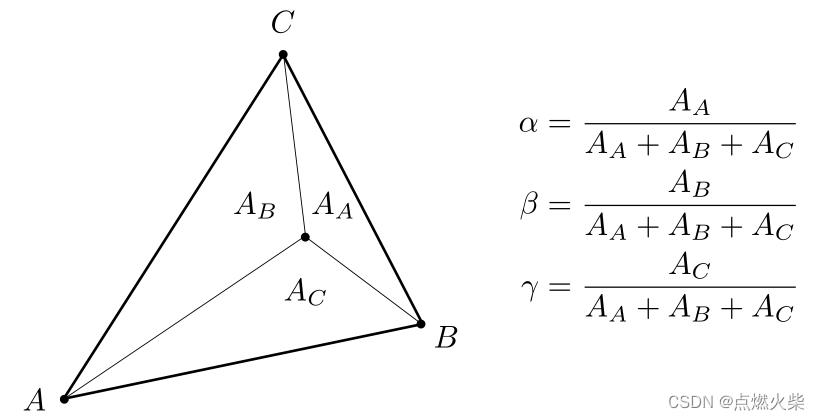
三角形的面积可以通过叉乘的方式获得，这里给出一个已经推导出来的公式，可直接通过该公式来计算重心坐标

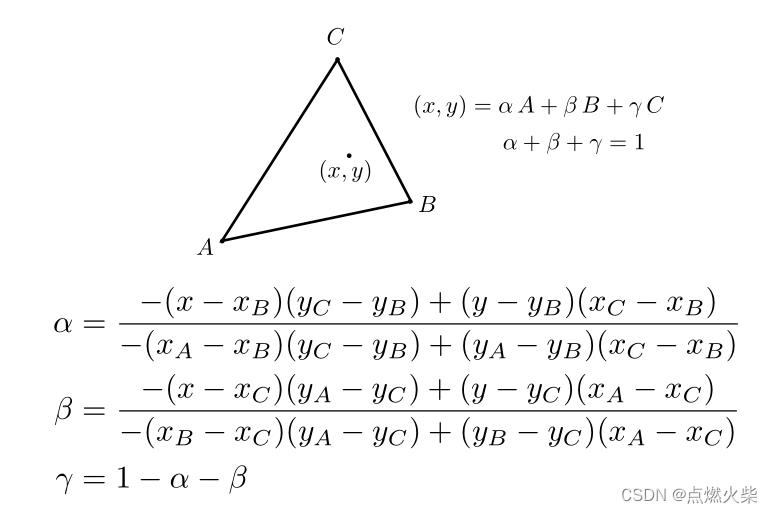
2.2 使用重心坐标做插值运算

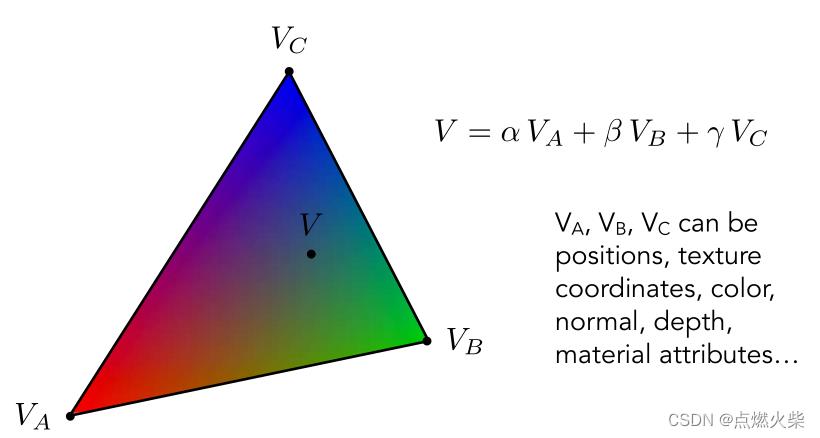
假设三角形中V点的重心坐标为(α,β,γ),一直三角形的三个顶点的坐标，这时可以通公式V=αA + βB + γ*C来得到V点的坐标
以上是以顶点为例通过插值的方式获取到三角形内任意一点的坐标，还有一些属性同样可以利用重心坐标插值计算获取三角形内任一点的属性值，比如颜色、法线、纹理坐标、深度(z-index)以及自定义的一些材质相关属性

注意：
投影变换前利用重心坐标插值和投影变换后插值结果是不一样的，插值运算是在三维空间中进行的，已经投影到屏幕上的坐标如何变回去？答案是利用投影矩阵的逆矩阵进行逆变换

建议：三维空间的属性需在三维空间中完成插值，然后在映射到二维中去

3 纹理映射常见问题

3.1 纹理太小

3.1.1 产生原因

例如要渲染一面墙，它的分辨率1024*1024，但与它对应的纹理大小是256x256，显然纹理相比于墙面过小了，当以墙面上一点去查询纹理时，可能查询到不准确的值，先来说说为什么会查询出不准确的值：
1.墙面的最小单位是像素(pixel)，纹理的最小单位为纹素(texel)
2.由于纹理过小，会存在多个像素查询纹理时返回同一个纹素
3.墙面渲染时每个像素取到的纹素不是连续变化的，渲染出来的墙面感觉像是一个个非常细小的格子组成，看上去不自然

3.1.2 解决办法

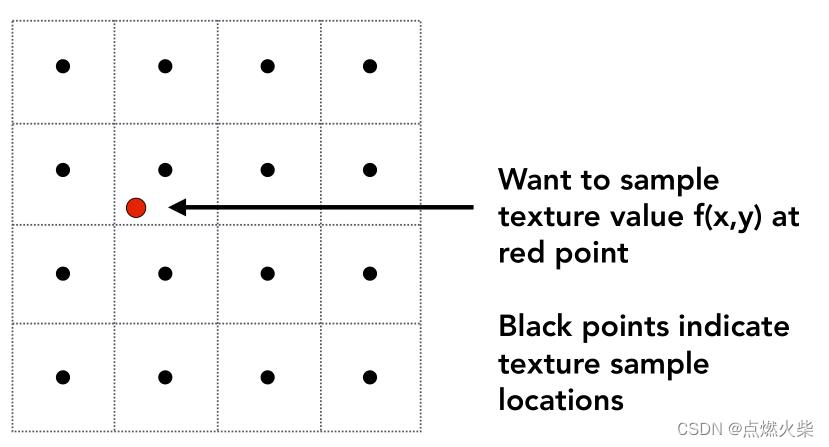
如上图，红点代表一个像素的中心点的位置，这个4*4的格子代表一个纹理，每个格子中心的黑点表示纹素的中心
一个像素映射到纹理的位置是红点的位置时如何查找出准确的值，正确的方式是使用双线性插值(Bilinear)，接下来说说双线性插值的处理过程：

1. 在纹理上找到与该像素映射位置临近的四个纹素u00、u01、u10、u11
   
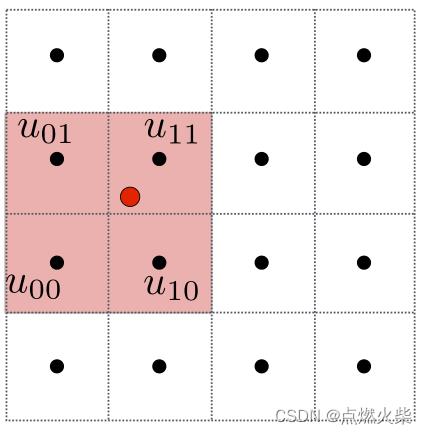
   2.以这四个点创建新的纹理坐标系，以u00到u10方向为u方向，u00到u01为v方向，这时可以指定在该坐标系中红点的位置是(s,t)
   
2. 第一次线性插值 (水平方向)，线性插值的公式如下
   
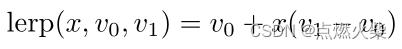
   这次的插值为了得到两个插值结果u0和u1，u0以s为当前值从u00和u10之间插值，u1以s为当前值从u01和u11之间插值
   
3. 第二次线性插值 (竖直方向)，有了上一步得到的结果u0和u1，在竖直方向以t为当前值从u0和u1之间插值，得到的结果就是我们要求的结果
   

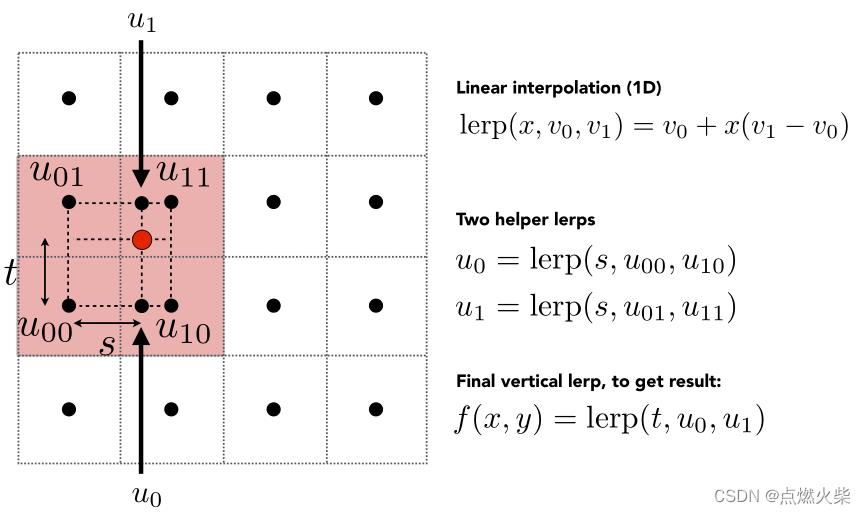
我们在水平方向做一次插值，在竖直方向做一次插值，因此这个方法叫双线性插值，这样就可以得到任意映射点的准确值,

纹理过小使用双线性插值的办法外，还有精度更高的处理办法叫双三次插值算法(Bicubic) 过程与双线性插值类似，但取的是周围16个texel，同样做竖直的和水平的插值，只不过每次用4个做三次的插值，而非线性的插值，运算量大一些，效果更好，通常高质量伴随高开销，实际双线性插值可以满足大多数需求

3.2 纹理太大

3.2.1 纹理太大的影响

通常纹理过大会引发更严重的问题，例如渲染一个格栅状地面，纹理是一个小格子，在地面的两个方向上重复平铺，远处的一个像素需要装进来更多的纹素，如果按照之前插值的方式处理，渲染出来的结果是远处出现摩尔纹，近处出现锯齿

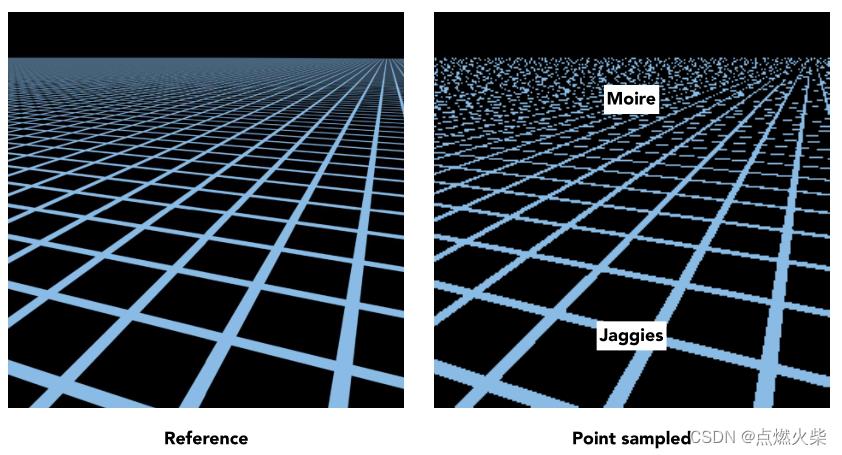
3.2.2 走样产生原因

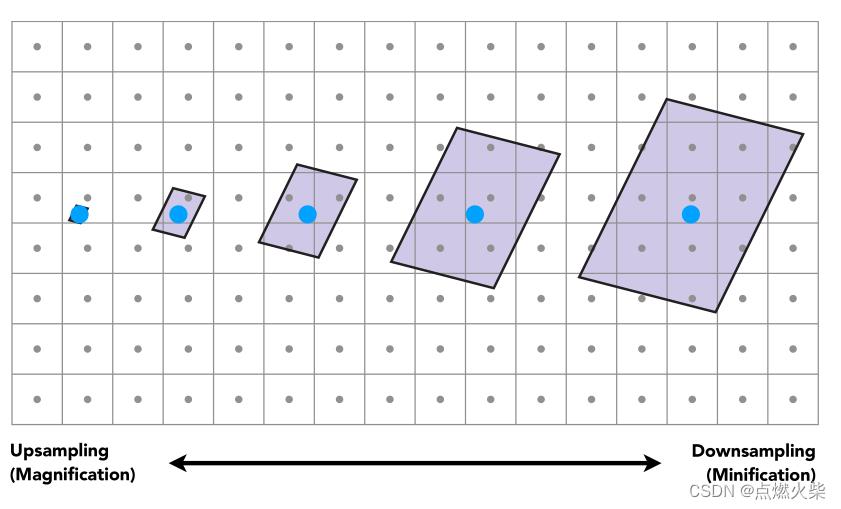
如上图，从左到右表示场景中与相机的距离由近到远，当比较近的时候屏幕上一个像素覆盖的面积大概是一个纹素的大小，随着与相机距离的变大，屏幕上一个像素所覆盖的纹理上的面积越来越大，通常每个纹素有自己的颜色，最远距离中覆盖了多个纹素，但只会进行一次采样，采样的结果自然不能代表原理那么多纹素的颜色，所以会出现走样现象

3.2.3 解决办法

3.2.3.1 超采样（MSAA）

例如把采样点增加到512，效果很不错，但是开销太大

3.2.3.2 MipMap

说MipMap前先阐述两个概念点查询和范围查询
点查询：以点为单位去纹理中查询对应位置的值，使用的双线性插值都是点查询
范围查询（Range Query）：不需要采样，给你任何一个区域，你立刻可以得到它内部的平均值；这就是范围查询，有很多种类，这里是查询平均值，也有查询范围内的最大值和最小值的范围查询
注意：MipMap 做范围查询时只有近似正方向的范围查询才是准确的
什么是MipMap，如下图，把一张纹理分成若干层，原始纹理为第0层，比如大小为128*128，每增加一层纹理分辨率缩小一半，直到缩小到只剩一个像素，那层数就是log2（纹理的长或宽）

相比原始图片的存储量，MipMap只增加了1/3的存储量
通常MipMap是在渲染前通过预计算完成的，生成对应层级的纹理，经过计算后MipMap变成如下图的结构，称为图像金字塔

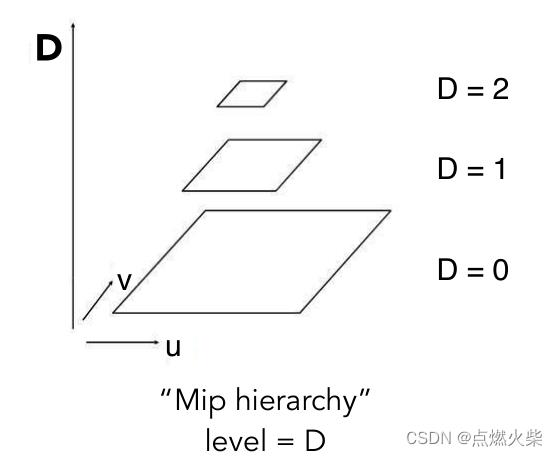
MipMap需要在方形区域内做范围查询，如何确定需要查询的区域呢

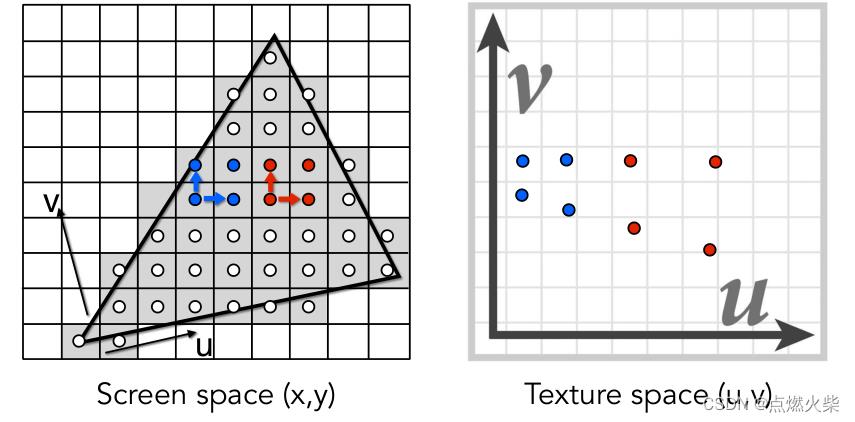
如上图，三角形覆盖了一些采样点，以红色点和蓝色点为例，它们会投影到纹理空间上，可以观察到它们围成的区域不在是正方形了

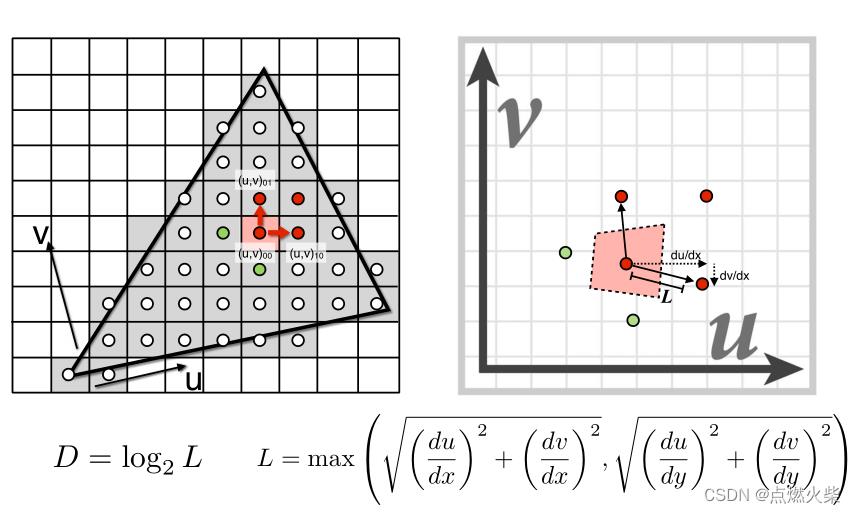
如上图，例如我们要确定红色点左下角的采样点(粉色区域)在纹理坐标上查询范围的大小，在纹理空间中以这个点为中心，连接上面和右面的采样点，求出距离，并取最大值，假设最大的长度是L

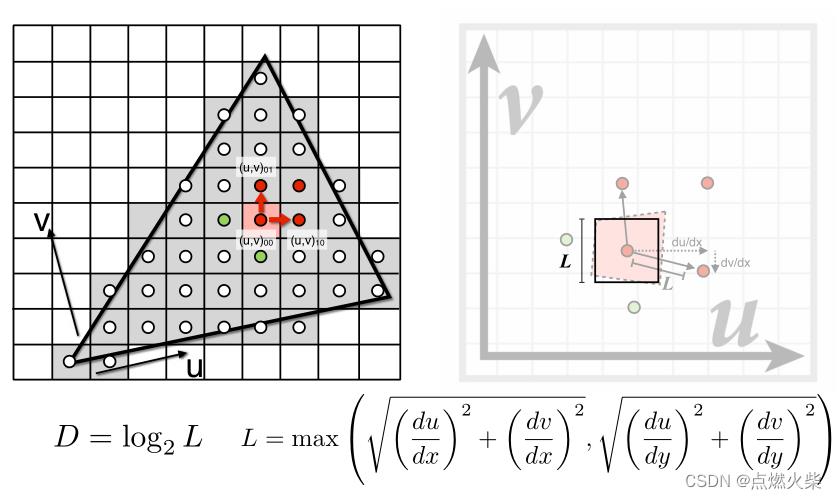
如上图，求出的长度L基本近似采样点（粉红色区域）映射在纹理上的正方向的长度
有了正方向的长度就可以通过公式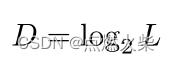来确定去那一层查询

直接利用层级去MinMap中查询出来的结果，会发现层级之间过渡非常生硬，不是平滑过渡，如下图（不同颜色代表不同层级）

这有什么好办法吗，答案是肯定的，还是插值，例如你需要查询1.3层，那先查询1层和2层，然后拿两个结果在做一次插值

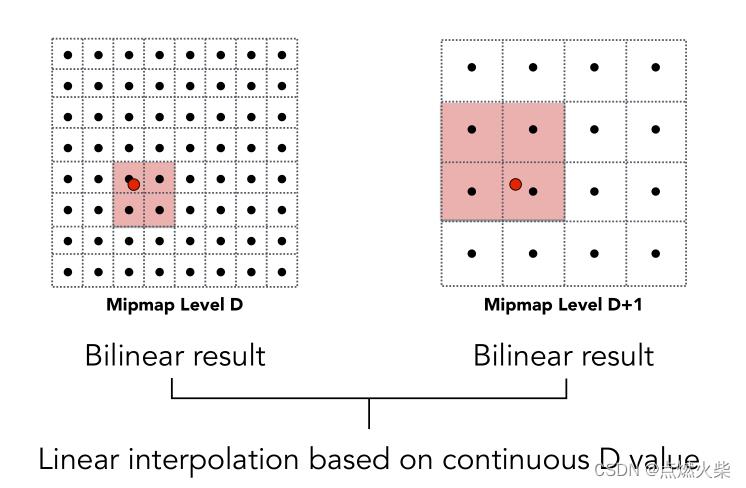
首先在D层使用双线性插值查询该点的值，然后继续使用双线性插值查询出D+1层的值，最后层与层之间做一次插值，我们把这种方法称为三线性插值

三线性插值需要做两次查询，一次插值，开销很小，并且效果也非常好如下图

3.2.3.3 MipMap的限制

如上图，使用MipMap处理的结果中会发现远处的细节全部都模糊掉了，这种现象称为模糊过度，问题出在哪了，在处理过程中，它只能查询方块区域，而我们查询的方块是近似得到的，所以是不完全准确的，既然问题出现如何解决，答案是使用各项异性过滤(Anisotropic Filtering)

各向异性过滤也就是RipMap，它和MipMap的不同之处就是它可以支持矩形区域的查询，生成出来的纹理如下

上图中， 沿着对角线上的图，水平方向和竖直方向上各缩小一半，称为各项同性，其实也就是MipMap
其余的有的只在水平方向发生压缩，有的只在竖直方向发生压缩，也有的在水平和竖直方向同时发生压缩且压缩比例可能会不一样，像这样在不同方向上它的表现各不相同称为各项异性。各向异性额外的开销是原本的三倍，造成较大的显存开销，能解决部分问题，只能满足矩形区域的范围查询，针对斜着的矩形区域（下图右侧中类似平行四边形）的查询也无能为力

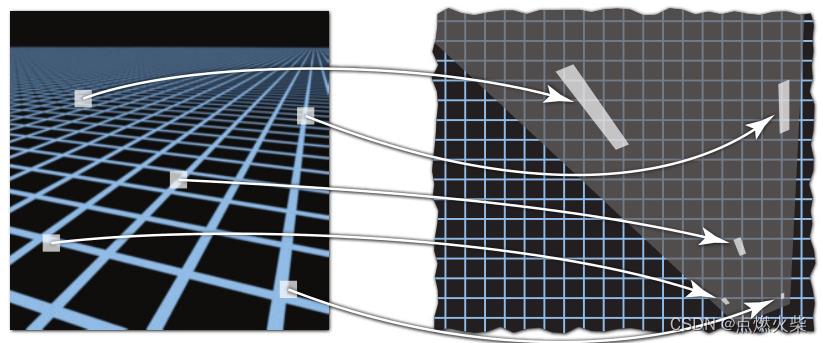
对于上述这类情况我们可以使用EWA Filtering来解决，不规则的形状都可以拆成很多个不同的圆形去覆盖，当然运算量又会增加。