基于差分迭代发求解离散微分方程的matlab仿真
Posted fpga和matlab
tags:
篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了基于差分迭代发求解离散微分方程的matlab仿真相关的知识，希望对你有一定的参考价值。
目录
一、理论基础
这类复杂方程组，其解方程通常不能直接使用MATLAB内部的自带函数进行求解，往往需要使用别的算法进行，本课题涉及到的方程组的基本类型如下所示：
“连续微分方程”到“离散微分方程”到“差分方程”，离散微分方程，变成差分方程。建立差分方程时，时间采用一阶显格式，空间采用一阶偏心差分格式。
二、MATLAB仿真程序
clc;
clear;
close all;
warning off;
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
Vj = 1.0e14*[2.037671762107052
2.034215151823580
2.030770248941575
2.027336994082841
2.023915328270042
2.020505192923336
2.017106529857023
2.013719281276238
2.010343389773680
2.006978798326360
2.003625450292398
2.000283289407840
1.996952259783514
1.993632305901912
1.990323372614108
1.987025405136702
1.983738349048801
1.980462150289017
1.977196755152515
1.973942110288066
1.970698162695152
1.967464859721083
1.964242149058149
1.961029978740801
1.957828297142857
1.954637052974735
1.951456195280716
1.948285673436231
1.945125437145175
1.941975436437247
1.938835621665319
1.935705943502825
1.932586352941177
1.929476801287208
1.926377240160643
1.923287621491580
1.920207897518015
1.917138020783374
1.914077944134078
1.911027620717132
1.907987003977725
1.904956047656871
1.901934705789056
1.898922932699921];
DVj = 1.0e+011*[3.462483877836962
3.450746652796573
3.439069007521719
3.427450539446898
3.415890849400914
3.404389541572597
3.392946223476911
3.381560505921475
3.370232002973479
3.358960331926962
3.347745113270506
3.336585970655279
3.325482530863469
3.314434423777078
3.303441282347068
3.292502742562887
3.281618443422334
3.270788026901764
3.260011137926652
3.249287424342494
3.238616536886035
3.227998129156823
3.217431857589106
3.206917381424041
3.196454362682216
3.186042466136488
3.175681359285135
3.165370712325313
3.155110198126804
3.144899492206068
3.134738272700597
3.124626220343543
3.114563018438641
3.104548352835411
3.094581911904646
3.084663386514161
3.074792470004828
3.064968858166864
3.055192249216406
3.045462343772321
3.035778844833293
3.026141457755156
3.016549890228479
3.007003852256406];
F_ASE_vj = [0.727687625579220
0.726884730352238
0.726081696237599
0.725278527912882
0.724475230042399
0.723671807275757
0.722868264249905
0.722064605587050
0.721260835896694
0.720456959773481
0.719652981799073
0.718848906541101
0.718044738553185
0.717240482375278
0.716436142533662
0.715631723540323
0.714827229893890
0.714022666078659
0.713218036565208
0.712413345810112
0.711608598256263
0.710803798332059
0.709998950452820
0.709194059019136
0.708389128418137
0.707584163022211
0.706779167191096
0.705974145268722
0.705169101586599
0.704364040461595
0.703558966196364
0.702753883079915
0.701948795386920
0.701143707377818
0.700338623299606
0.699533547384828
0.698728483851725
0.697923436905154
0.697118410735281
0.696313409518148
0.695508437416143
0.694703498577095
0.693898597135282
0.693093737210495];
O12_vj = 1.0e-24*[ 0.11
0.13
0.175
0.215
0.3
0.275
0.288
0.31
0.33
0.34
0.335
0.33
0.335
0.33
0.303
0.28
0.25
0.25
0.248
0.26
0.268
0.28
0.325
0.425
0.57
0.628
0.53
0.426
0.388
0.35
0.31
0.25
0.24
0.22
0.195
0.17
0.15
0.14
0.118
0.1
0.078
0.068
0.06
0.059];
O21_vj = 1.0e-24*[ 0.05
0.06
0.07
0.095
0.11
0.13
0.15
0.16
0.18
0.2
0.21
0.218
0.23
0.231
0.23
0.228
0.217
0.218
0.225
0.246
0.275
0.318
0.378
0.51
0.76
0.89
0.725
0.638
0.618
0.58
0.527
0.485
0.49
0.475
0.42
0.39
0.365
0.346
0.305
0.262
0.221
0.195
0.17
0.169];
%参数初始化
Vp = 3.074794441025641e14;
Vs = 1.955593333333334e14;
DVs = 3.186042466136488e11;
h = 6.626e-34;
Ac = 10.5625e-12;
Fp = 0.8773;
Fs = 0.7078;
NEr = 1.5e26;
NYb = 1.9e27;
O12_vs = 6.5e-25;
O21_vs = 9.0e-25;
O13_vp = 2.58e-25;
O31_vp = 0;
O12Yb_vp= 1.0e-24;
O21Yb_vp= 1.0e-24;
r21 = 7.9e-3; A21 = 1/r21;
r32 = 1.0e-9; A32 = 1/r32;
r43 = 1.0e-9; A43 = 1/r43;
r21Yb = 2.0e-3; A21Yb = 1/r21Yb;
C2 = 5.0e-23;
C3 = 5.0e-23;
C14 = 3.5e-23;
Ktr = 2.0e-22;
Kba = 0;
ap = 0;
as = 0;
M = 44;
%其余参数初始化
L = 0.05; %空间长度
time = 1e-8; %时间长度
Nz = 100; %空间点数
Nt = 100; %时间网点数
dt = time/Nt;%t微分导数累计量
dz = L/Nz;%z微分导数累计量
N1 = zeros(Nz,Nt);
N2 = zeros(Nz,Nt);
N3 = zeros(Nz,Nt);
N4 = zeros(Nz,Nt);
N1_Yb = zeros(Nz,Nt);
N2_Yb = zeros(Nz,Nt);
Ps = zeros(Nz,Nt);
PASE_plus = zeros(M,Nz,Nt);
PASE_minus = zeros(M,Nz,Nt);
Pp_plus = zeros(Nz,Nt);
Pp_minus = zeros(Nz,Nt);
G = zeros(Nz,Nt);
NF = zeros(Nz,Nt);
%方程组1的式子1复杂系数的参数表示
W11 = Fp*O13_vp/(Ac*h*Vp);
W12 = Fs*O12_vs/(Ac*h*Vs);
for i = 1:M
W13(i) = F_ASE_vj(i) * O12_vj(i) / (Ac*h*Vj(i));
end
W14 = Fs*O21_vs/(Ac*h*Vs);
for i = 1:M
W15(i) = F_ASE_vj(i) * O21_vj(i) / (Ac*h*Vj(i));
end
W16 = Fp*O31_vp/(Ac*h*Vp);
%方程组1的式子2复杂系数的参数表示
W21 = Fs*O12_vs/(Ac*h*Vs);
for i = 1:M
W22(i) = F_ASE_vj(i) * O21_vj(i) / (Ac*h*Vj(i));
end
W23 = Fs*O21_vs/(Ac*h*Vs);
for i = 1:M
W24(i) = F_ASE_vj(i) * O21_vj(i) / (Ac*h*Vj(i));
end
%方程组1的式子3复杂系数的参数表示
W31 = Fp*O13_vp/(Ac*h*Vp);
W32 = Fp*O31_vp/(Ac*h*Vp);
%方程组1的式子4复杂系数的参数表示
W41 = Fp*O12Yb_vp/(Ac*h*Vp);
W42 = Fp*O21Yb_vp/(Ac*h*Vp);
Ps(1,:) = ones(1,Nt);
Pp_plus(1,:) = ones(1,Nt);
Pp_minus(1,:) = ones(1,Nt);
for j = 1:Nt-1
for i = 1:Nz-1
%方程组1式子1
N1(i,j+1) = N1(i,j) + ...
dt*( -1*(W11*(Pp_plus(i,j) + Pp_minus(i,j)) + W12*Ps(i,j) + sum(W13.*(PASE_plus(:,i,j)+PASE_minus(:,i,j))'))*N1(i,j) +...
(A21 + W14*Ps(i,j) + sum(W15.*(PASE_plus(:,i,j)+PASE_minus(:,i,j))'))*N2(i,j) + ...
C2*N2(i,j)^2 + W16*(Pp_plus(i,j) + Pp_minus(i,j))*N3(i,j) + C3*N3(i,j)^2 - C14*N1(i,j)*N4(i,j)+...
-1*Ktr*N2_Yb(i,j)*N1(i,j)+Kba*N1_Yb(i,j)*N3(i,j) );
%方程组1式子2
N2(i,j+1) = N2(i,j) + ...
dt*( (W21*Ps(i,j)+sum(W22.*(PASE_plus(:,i,j)+PASE_minus(:,i,j))'))*N1(i,j) +...
-1*(A21 + W23*Ps(i,j) + sum( W24.*(PASE_plus(:,i,j)+PASE_minus(:,i,j))' ))*N2(i,j) +...
A32*N3(i,j) - 2*C2*N2(i,j)^2 + 2*C14*N1(i,j)*N4(i,j) );
%方程组1式子3
N3(i,j+1) = N3(i,j) + ...
dt*( W31*(Pp_plus(i,j) + Pp_minus(i,j))*N1(i,j) - A32*N3(i,j) - W32*(Pp_plus(i,j) + Pp_minus(i,j))*N3(i,j) -...
2*C3*N3(i,j)^2 + A43*N4(i,j) + Ktr*N2_Yb(i,j)*N1(i,j) - Kba*N1_Yb(i,j)*N3(i,j) );
%方程组1式子4
N1_Yb(i,j+1) = N1_Yb(i,j) + ...
dt*(-1*W41*(Pp_plus(i,j) + Pp_minus(i,j))*N1_Yb(i,j) + W42*(Pp_plus(i,j) + Pp_minus(i,j))*N2_Yb(i,j) +...
A21Yb*N2_Yb(i,j) + Ktr*N2_Yb(i,j)*N1(i,j) - Kba*N1_Yb(i,j)*N3(i,j));
%方程组1式子5
N4(i,j+1) = NEr - (N1(i,j+1) + N2(i,j+1) + N3(i,j+1));
%方程组1式子6
N2_Yb(i,j+1) = NYb - N1_Yb(i,j+1);
if N1(i,j+1) > NEr,N1(i,j+1) = NEr;end
if N2(i,j+1) > NEr,N2(i,j+1) = NEr;end
if N3(i,j+1) > NEr,N3(i,j+1) = NEr;end
if N4(i,j+1) > NEr,N4(i,j+1) = NEr;end
if N1_Yb(i,j+1) > NYb,N1_Yb(i,j+1) = NYb;end
if N2_Yb(i,j+1) > NYb,N2_Yb(i,j+1) = NYb;end
if N1(i,j+1) < 0,N1(i,j+1) = 0;end
if N2(i,j+1) < 0,N2(i,j+1) = 0;end
if N3(i,j+1) < 0,N3(i,j+1) = 0;end
if N4(i,j+1) < 0,N4(i,j+1) = 0;end
if N1_Yb(i,j+1) < 0,N1_Yb(i,j+1) = 0;end
if N2_Yb(i,j+1) < 0,N2_Yb(i,j+1) = 0;end
%由以上方程计算得到的N1，N2，N3，N4，N1Yb，N2Yb
%方程组2
Pp_plus(i+1,j) = Pp_plus(i,j) + dz*(-Fp*(O13_vp*N1(i,j) - O31_vp*N3(i,j) + O12Yb_vp*N1_Yb(i,j) - O21Yb_vp*N2_Yb(i,j))*Pp_plus(i,j) - ap*Pp_plus(i,j));
Pp_minus(i+1,j) = Pp_minus(i,j) + dz*(Fp*(O13_vp*N1(i,j) - O31_vp*N3(i,j) + O12Yb_vp*N1_Yb(i,j) - O21Yb_vp*N2_Yb(i,j))*Pp_minus(i,j) + ap*Pp_plus(i,j));
Ps(i+1,j) = Ps(i,j) + dz*(Fs*( O21_vs*N2(i,j) - O12_vs*N1(i,j) )*Ps(i,j) - as*Ps(i,j));
%PASE_plus = zeros(M,Nz,Nt);
%PASE_minus = zeros(M,Nz,Nt);
for ii = 1:M
PASE_plus(ii,i+1,j) = PASE_plus(ii,i,j)+dz*(F_ASE_vj(ii)*( O21_vj(ii)*N2(i,j) - O12_vj(ii)*N1(i,j) ) * PASE_plus(ii,i,j) +...
2*h*Vj(ii)*DVj(ii)*F_ASE_vj(ii)*O21_vj(ii)*N2(i,j)-as*PASE_plus(ii,i,j));
PASE_minus(ii,i+1,j) = PASE_minus(ii,i,j)+dz*(-1*F_ASE_vj(ii)*( O21_vj(ii)*N2(i,j) - O12_vj(ii)*N1(i,j) ) * PASE_minus(ii,i,j) -...
2*h*Vj(ii)*DVj(ii)*F_ASE_vj(ii)*O21_vj(ii)*N2(i,j)+as*PASE_minus(ii,i,j));
end
if Pp_plus(i+1,j) < 0,Pp_plus(i+1,j) = 0;end
if Pp_minus(i+1,j) < 0,Pp_minus(i+1,j) = 0;end
if Ps(i+1,j) < 0,Ps(i+1,j) = 0;end
%通过稳态计算得到Pp+，Pp-，Pase+，Pase-，Ps
end
end
for z = 1:Nz
for t = 1:Nt
PASE_plus2(z,t) = sum(PASE_plus(:,z,t));
PASE_minus2(z,t) = sum(PASE_minus(:,z,t));
end
end
for z = 1:Nz
for t = 1:Nt
G(z,t) = 10*log10(Ps(z,t)/Ps(1,1));
end
end
for z = 1:Nz
for t = 1:Nt
NF(z,t) = 10*log10(1/G(z,t) + PASE_plus2(z,t)/(G(z,t)*Vs*DVs) );
end
end
%计算得到N1~t，N2~t，N3~t，N4~t，........
figure;
subplot(221);
plot(N1(1,2:end),'b-','LineWidth',2);
xlabel('t');
ylabel('N1(Z)');
title('N1(Z)&t');
grid on;
subplot(222);
plot(N2(1,2:end),'b-','LineWidth',2);
xlabel('t');
ylabel('N2(Z)');
title('N2(Z)&t');
grid on;
subplot(223);
plot(N3(1,2:end),'b-','LineWidth',2);
xlabel('t');
ylabel('N3(Z)');
title('N3(Z)&t');
grid on;
subplot(224);
plot(N4(1,2:end),'b-','LineWidth',2);
xlabel('t');
ylabel('N4(Z)');
title('N4(Z)&t');
grid on;
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
figure;
subplot(211);
plot(N1_Yb(1,2:end),'b-','LineWidth',2);
xlabel('t');
ylabel('N1Yb(Z)');
title('N1Yb(Z)&t');
grid on;
subplot(212);
plot(N2_Yb(1,2:end),'b-','LineWidth',2);
xlabel('t');
ylabel('N2Yb(Z)');
title('N2Yb(Z)&t');
grid on;
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
figure;
subplot(211);
plot(PASE_plus2(3,1:end-2),'b-','LineWidth',2);
xlabel('t');
ylabel('PASE+(Z)');
title('PASE+(Z)&t');
grid on;
subplot(212);
plot(PASE_minus2(3,1:end-2),'b-','LineWidth',2);
xlabel('t');
ylabel('PASE-(Z)');
title('PASE-(Z)&t');
grid on;
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
figure;
plot(Ps(2,1:end-1),'b-','LineWidth',2);
xlabel('t');
ylabel('Ps(Z)');
title('Ps(Z)&t');
grid on;
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
figure;
subplot(211);
plot(Pp_plus(20,3:end-1),'b-','LineWidth',2);
xlabel('t');
ylabel('Pp+(Z)');
title('Pp+(Z)&t');
grid on;
subplot(212);
plot(Pp_minus(20,3:end-1),'b-','LineWidth',2);
xlabel('t');
ylabel('Pp-(Z)');
title('Pp-(Z)&t');
grid on;
figure;
subplot(211);
plot(Pp_plus(1:end,6),'b-','LineWidth',2);
xlabel('t');
ylabel('Pp+(Z)');
title('Pp+(Z)&t');
grid on;
subplot(212);
plot(Pp_minus(1:end,6),'b-','LineWidth',2);
xlabel('t');
ylabel('Pp-(Z)');
title('Pp-(Z)&t');
grid on;
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
figure;
plot(G(20,3:end-1),'b-','LineWidth',2);
xlabel('t');
ylabel('G(Z)dB');
title('G(Z)&t');
grid on;
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
figure;
plot(NF(2,3:end-1),'b-','LineWidth',2);
xlabel('t');
ylabel('NF(Z)dB');
title('NF(Z)&t');
grid on;
三、仿真结果
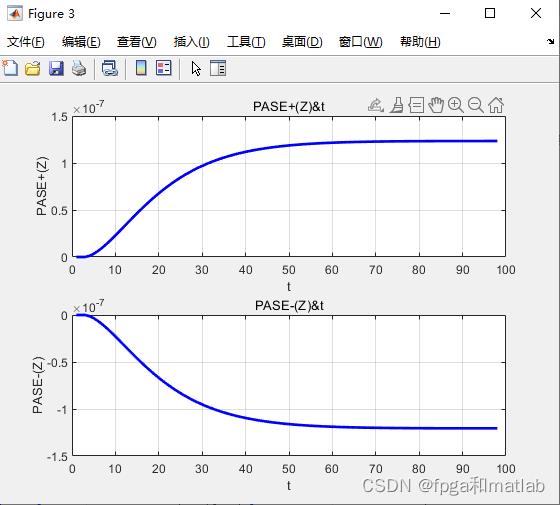
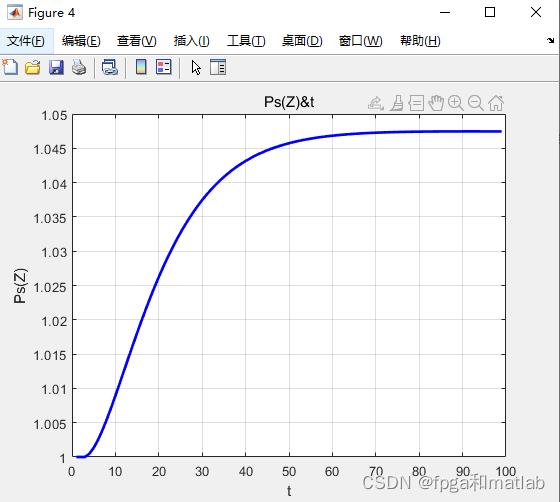
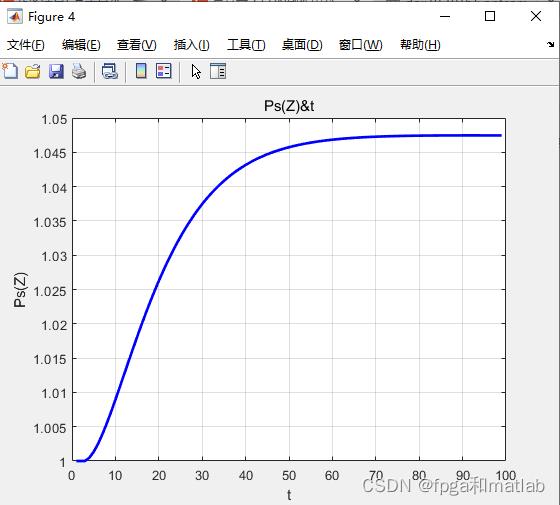
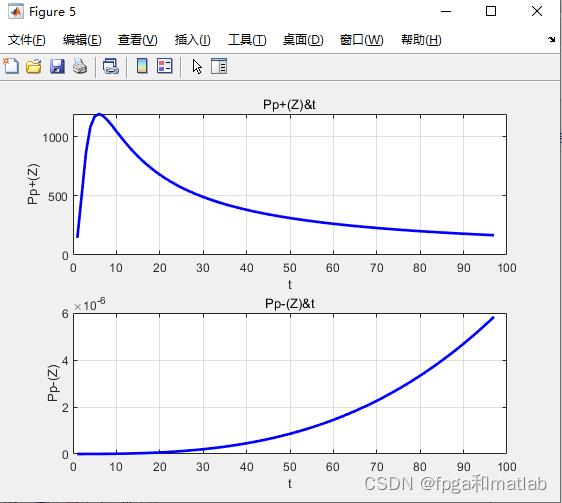
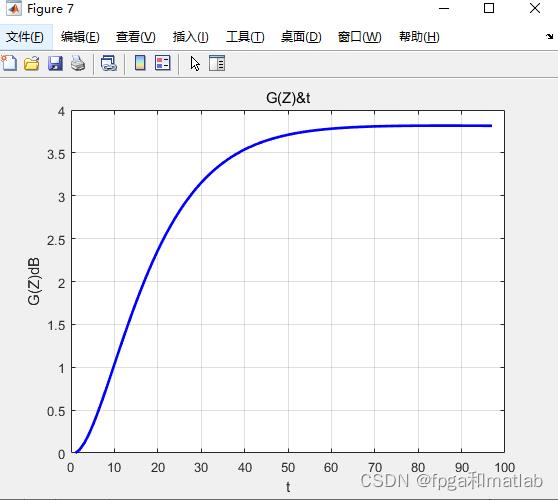
A16-15
以上是关于基于差分迭代发求解离散微分方程的matlab仿真的主要内容，如果未能解决你的问题，请参考以下文章
Runge-Kutta龙格-库塔法求解微分方程matlab仿真
基于龙格-库塔法Runge-Kutta的常微分方程的求解matlab仿真
MATLAB教程案例85通过matlab实现有限差分法求解微分方程
数字信号处理线性常系数差分方程 ( 卷积 与 “ 线性常系数差分方程 “ | 使用 matlab 求解 “ 线性常系数差分方程 “ )