迪杰斯特拉（Dijkstra)算法

Posted 2022-09-16 森明帮大于黑虎帮

基本思想

Dijkstra算法是一种典型的最短路径搜索算法，和之前的BFS和DFS算法类似，Dijkstra本质上是一种BFS搜索算法。

一般步骤如下：

1. 建立两个集合S和U，S中存放已经确定了最短距离的点，U中放未放入S中的点。
2. 在S中push起始点，U中放入其他的点。
3. 计算U中的所有点到起点之间的距离，起点与起点之间的距离记为0，与集合S中的点不相邻的点距离记为无穷大，将计算出的距离起点最近的点k放入集合S中，同时从集合U中移除点k。
4. 重复上一步骤直到遍历完集合U中的所有点。

实际步骤

如图:

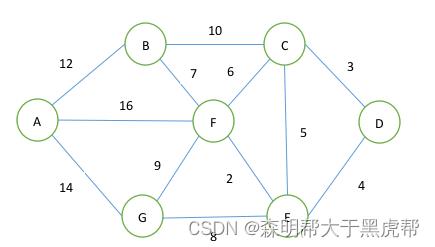
从图中，可以看出，各个顶点的名字以及顶点之间的距离大小，我们现在选取点D为起始点，则有：

第一步，选取点D作为起始点，此时

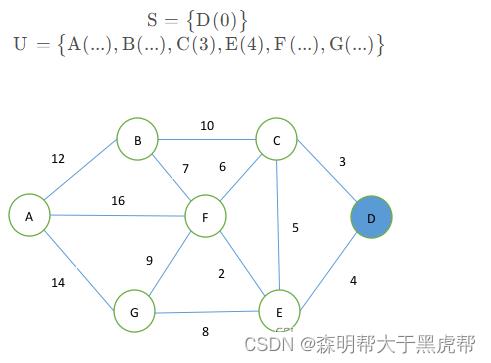
第二步，从集合U中取出与起始点距离最近的点C，并将其放入集合S，同时更新集合U中各个点到起始点D之间的距离，13 l_bcd=13l , l_fcd=9l ,l_ecd=8l ,这里需要注意的是，点E与点D直接相连，且l_ed=4l ,因此点E到起始点最小的距离为4，集合U中点E不更新距离。

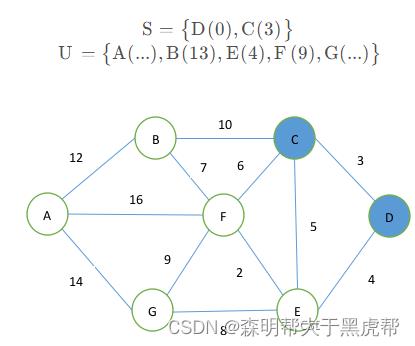
第三步，继续重复上一步，从集合U中取出距离值最小的点E，放入集合S中，同时更新集合U中各个点与起始点之间的距离，l f e l_fed=6l ， l_ged=12l ，更新集合U，有

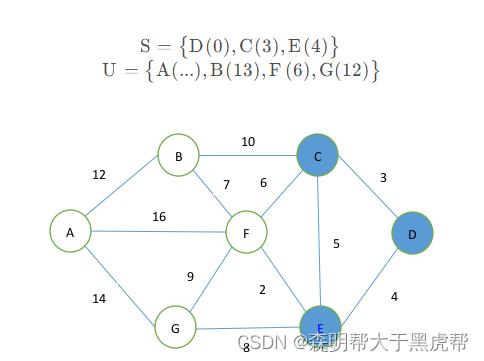
第四步，从集合U中取出点F放入集合S，同时更新集合U中的各个点的距离，l_afed=22l ， l_bcd=13l ， l_ged=12l

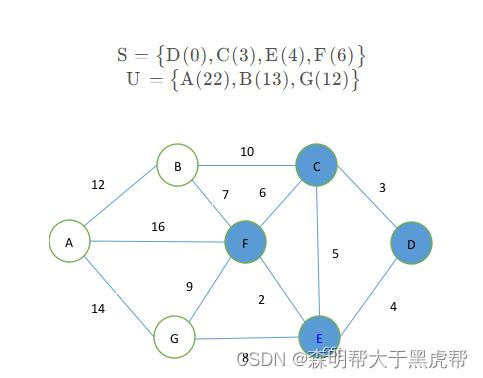
​ 第五步，从集合U中取出点G放入集合S，同时更新集合U中的各点到起始点的距离，

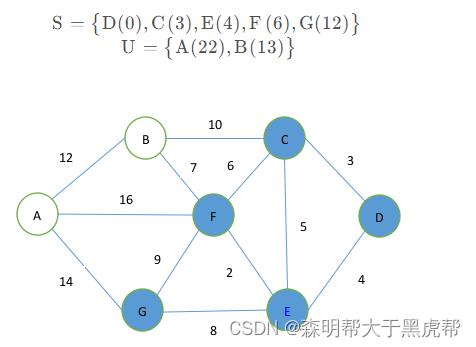
第六步，从集合U中取出点B放入集合S中，同时更新集合U中的各点到起始点的距离，

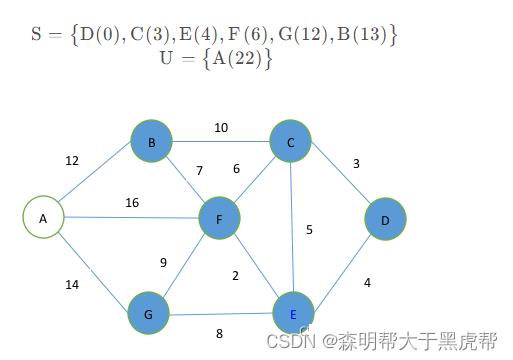
第七步，将点A从集合U中取出放入集合S，此时集合U为空。

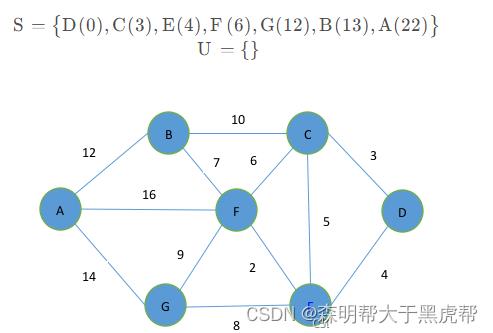
总结

看完以上步骤可以看出，Dijkstra算法的核心思想就是按照从小到大的顺序，使用BFS搜索出图中各个点到起始点之间的距离。
以第四步来说，在集合S中放入点F后，集合U中与点F相邻的点有A,B,G三个点，分别对这个三个点，进行BFS搜索，找出这三个点通过集合S中的点能达到起始点D的最短距离，然后再进行下一步。

每个点的具体搜索方式：

1. 第四步放入的点为F，取邻点G为例，点G与集合S中的点F,点E均相邻，其中 l_gf=9l ，l_ge=8l 。

2. 这样先从点E进行搜索，点E与点F,C,D相连，由于用的时BFS，去掉点F， L_ed=4， L_ec=5，此时点G到点D的一条路径已搜索到，GED距离为12，此时还有点C，GECD距离为16，则目前最短路径为GED(12)；

3. 对点F进行BFS搜索，找到此时最短路径，GFED(15)，与上一步进行对比，最短路径仍为GED。
   单个点完成BFS后，在进行下一个点，直到更新此步所有的点。

优点

可以搜索图中的所有的点，并且找到每个点到起始点的最优解。

缺点

只能看到当前步骤的路径最优，并非是全局最优，并且下一次搜索的方向并不确定；
无法提供当前的位置信息。