机器学习Logistic 分类回归算法 (二元分类 & 多元分类)
Posted 计算机魔术师
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了机器学习Logistic 分类回归算法 (二元分类 & 多元分类)相关的知识,希望对你有一定的参考价值。

🤵♂️ 个人主页: @计算机魔术师
👨💻 作者简介:CSDN内容合伙人,全栈领域优质创作者。
该文章收录专栏
✨— 机器学习 —✨
【机器学习】logistics分类
一、线性回归能用于分类吗?
l o g i s t i c logistic logistic(数理逻辑)回归算法(预测离散值 y y y 的 非常常用的学习算法
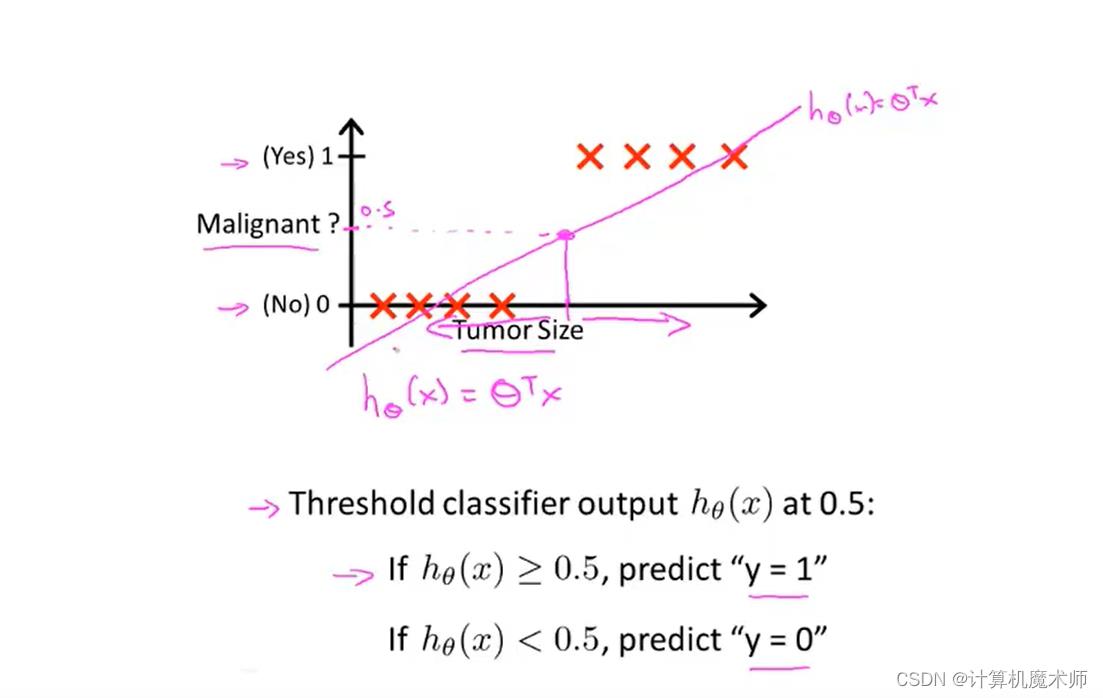
假设有如下的八个点( y = 1 或 0 ) y=1 或 0) y=1或0),我们需要建立一个模型得到准确的判断,那么应该如何实现呢
- 我们尝试使用之前文章所学的线性回归 h θ ( x ) = θ T ∗ x h_\\theta(x) = \\theta^T*x hθ(x)=θT∗x 来拟合数据( θ \\theta θ是参数列向量,注意这里的 x x x是关于 x i x_i xi的向量,其中 x 0 = 1 , 即 x 0 ∗ θ 0 = 常数项 x_0=1, 即 x_0*\\theta_0 = 常数项 x0=1,即x0∗θ0=常数项),并在0~1设置一个阈值 y = 0.5 所对应的 x 0.5 值 y = 0.5 所对应的 x_0.5 值 y=0.5所对应的x0.5值, x x x 大于 x 0.5 x_0.5 x0.5 的点则为1,否则为0,预测会得到如下粉丝直线,
上一篇文章: 【机器学习】浅谈正规方程法&梯度下降
假设我们再增加一个数据点,如下图右方,按照如上算法对应的拟合直线
h
θ
(
x
)
h_\\theta(x)
hθ(x)则如下蓝色直线,此时得到错误的预测 (对于结果为1也小于
x
0.5
x_0.5
x0.5)
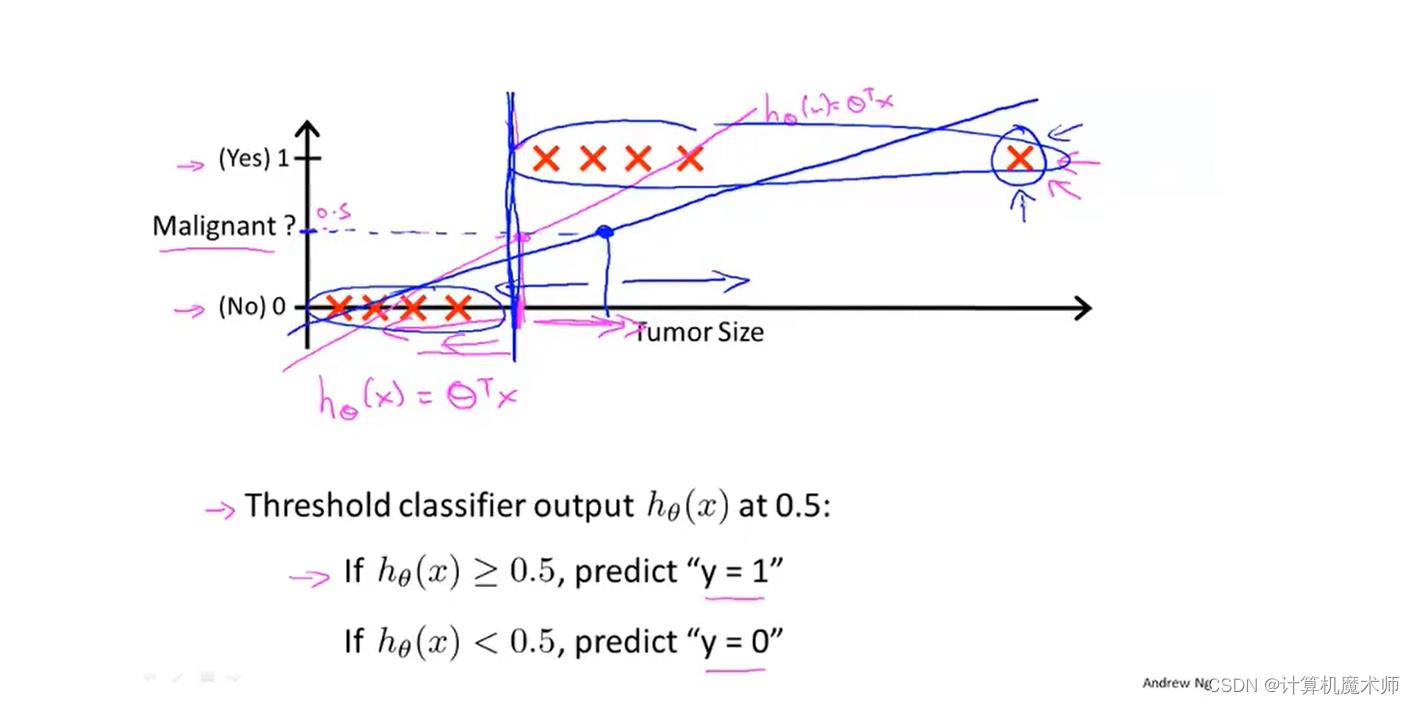
所以综上所诉,用线性回归来用于分类问题通常不是一个好主意,并且线性回归的值会远远偏离0或1,这显示不太合理。
所以梯度下降算法中引出 logistic regression 算法
二、二元分类
2.1假设函数
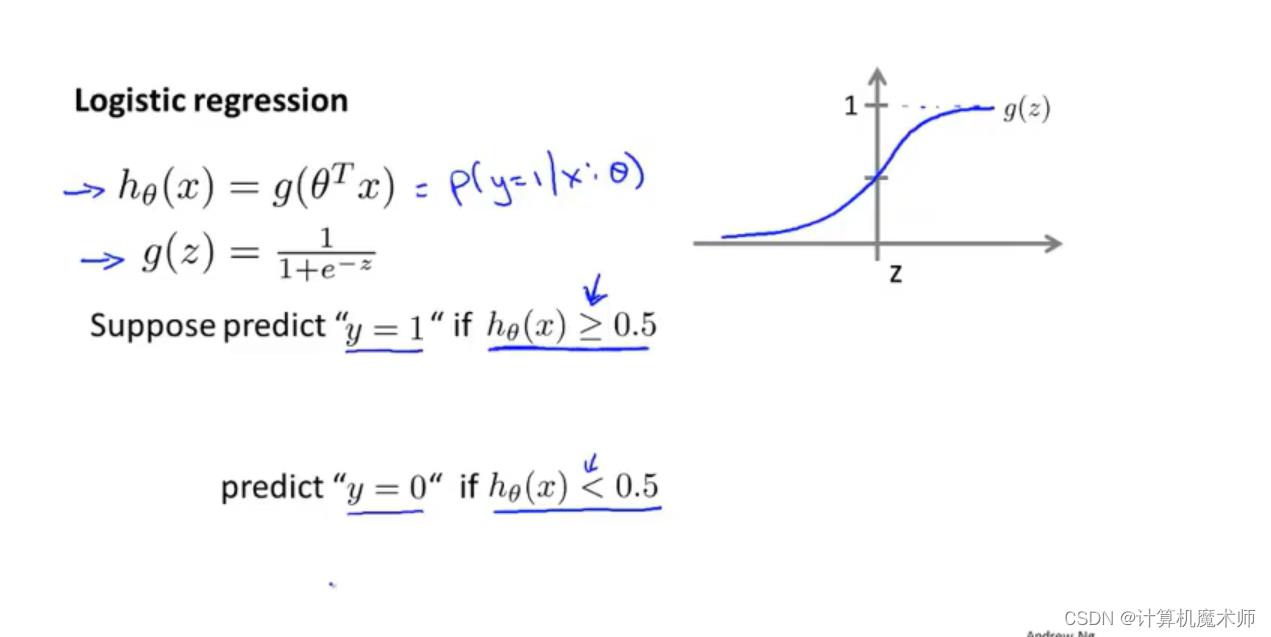
我们希望能把 h θ ( x ) = θ T ∗ x h_\\theta(x) = \\theta^T*x hθ(x)=θT∗x 结果在 0 ~ 1 之间,
这里引入 s i g m o i d sigmoid sigmoid 函数 (也叫做 l o g i s t i c logistic logistic 函数) —— g ( x ) = 1 1 + e − x g(x) = \\frac11 + e ^-x g(x)=1+e−x1
s i g m o i d sigmoid sigmoid函数图像是一个区间在 0 ~ 1的S型函数, x ⇒ ∞ x \\Rightarrow\\infty x⇒∞则 y ⇒ 1 y\\Rightarrow1 y⇒1, x ⇒ − ∞ x \\Rightarrow-\\infty x⇒−∞则 y ⇒ 0 y\\Rightarrow0 y⇒0

- 令
h
θ
(
x
)
=
g
(
θ
T
∗
x
)
=
1
1
+
e
−
θ
T
∗
x
h_\\theta(x) =g( \\theta^T*x) = \\frac11 + e ^- \\theta^T*x
hθ(x)=g(θT∗x)=1+e−θT∗x1
那么我们的函数结果结果就会在0 ~ 1 之间
那现在我们所要做的便是需要求得参数 θ \\theta θ 拟合模型
如下图,假设肿瘤案例,如下 x x x为一个病人 同样的用列向量表示 x x x的参数,那么参数一tumorSize便是肿瘤的大小,那么我们可以假设输出结果为 0.7 ,意思就是医生会告诉这个病人很不幸,会有很大(70%)的概率得到肿瘤。
- 那么公式可以表示为 h θ ( x ) = P ( y = 1 ∣ x ; θ ) h_\\theta(x) = P(y=1|x;\\theta) hθ(x)=P(y=1∣x;θ)
- 即在 x x x的条件下 求给定 y y y (概率参数为 θ \\theta θ)的概率

那么在
y
y
y只有 0 和 1 的情况下,有如下公式 (二者为对立事件,符合全概率公式)
- P ( y = 1 ∣ x ; θ ) + P ( y = 0 ∣ x ; θ ) = 1 P(y=1|x;\\theta)+ P(y=0 |x;\\theta)= 1 P(y=1∣x;θ)+P(y=0∣x;θ)=1
- 1 − P ( y = 0 ∣ x ; θ ) = P ( y = 1 ∣ x ; θ ) 1 - P(y=0 |x;\\theta)= P(y=1|x;\\theta) 1−P(y=0∣x;θ)=P(y=1∣x;θ)
概率结果只在0 ~ 1中
- 假设如下
那么此时我们可以设置阈值 g ( z ) g(z) g(z) = 0.5,大于 0.5 的点则为1,否则为0
即在 z < 0 z<0 z<0(即 θ T ∗ x \\theta^T*x θT∗x)中 g ( z ) g(z) g(z)< 0.5, 此时预测为0,在 z > 0 z>0 z>0(即 θ T ∗ x \\theta^T*x θT∗x) 时, g ( z ) > 0 g(z)>0 g(z)>0 预测值为1
2.1.1 案例一

我们假设他的各个
θ
\\theta
θ 参数向量参数为-3,1,1
此时如果满足
g
(
z
)
g(z)
g(z)> 0.5 , 也就是横坐标
z
z
z(这里的
z
z
z 是对应线性方程) 大于零,预测 y 为 1 条件则如下:
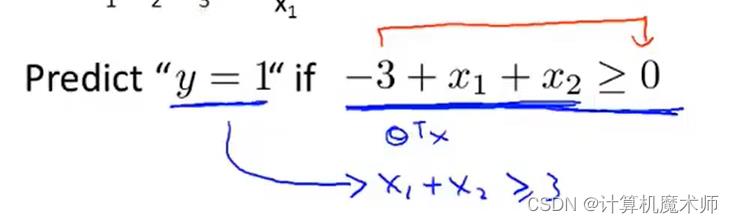
化简为条件
x
1
+
x
2
>
=
3
x_1 + x_2 >=3
x1+x2>=3 , 这个条件所对应的几何意义:
即一条切割线的右侧,此时
s
i
g
o
m
i
d
函数的
z
坐标
>
0
sigomid函数的z坐标>0
sigomid函数的z坐标>0 , y值 大于0.5
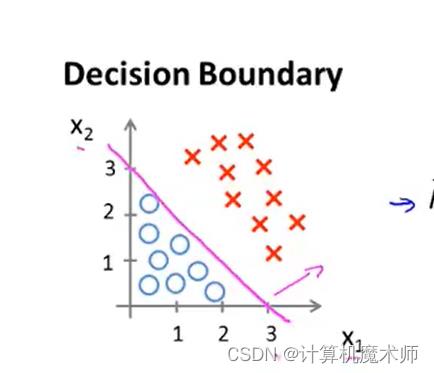
此时该切割线分割除了两个区域,分别是
y
=
0
与
y
=
1
y=0 与 y=1
y=0与y=1的 情况,我们把这条边界,称为决策边界,这些都是关于假设函数的属性,决定于其参数,与数据集属性无关

2.1.2例子二
有数据集如下:
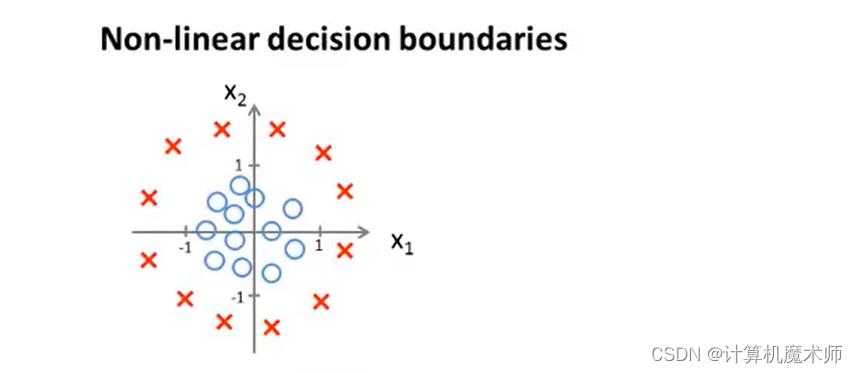
我们假设函数为多项式高阶函数,并对其参数假设赋值如下。

那我们的预测y=1时,
s
i
g
o
m
i
d
sigomid
sigomid横坐标
z
z
z满足条件为
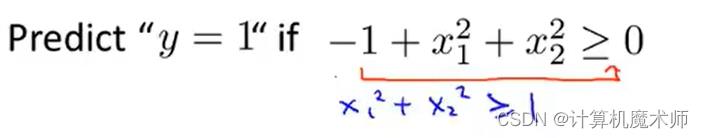
可以得到其决策边界decision boundory ——
x
1
2
+
x
2
2
=
1
x_1^2+x_2^2 =1
x