分治算法

Posted 2022-09-14 dotNET跨平台

1.概要

分治算法是一种很重要的算法。字面上的解释是“分而之治”，就是把一个复杂的问题分成两个或更多的相同问题或相似的子问题，再把子问题分成更小的子问题...知道最后子问题可以简单的直接求解，原问题的解即子问题的解的合并。这个技巧是很多搞笑算法的基础，如排序算法（快速排序，并归排序），傅立叶变换（快速傅立叶变换）...

分治算法可以求解的一些经典问题：

• 二分搜索

• 大整数乘法

• 棋盘覆盖

• 合并排序

• 快速排序

• 线性时间选择

• 最接近点对问题

• 循环赛日程表

• 汉诺塔

分治算法的基本步骤

分治法在每一层递归上都有三个步骤：

（1）分解：将原问题分解为若干个规模较小，相互独立，与原问题形式相同的子问题。

（2）解决：若子问题规模较小而容易被解决则直接解，否则递归的解各个子问题。

（3）合并：将各个子问题的解合并为原问题的解。

分治（Divide-and-conquer(P)）算法设计模式如下：

if|P|<n0

  then return(ADHOC(P))

//将P分解为较小的子问题P1,P2,...,Pk

for i <- 1 to k

do yi <- Divide-and-conquer(Pi) 递归解决Pi

T <- MERGE(y1,y2,...,yk)合并子问题

return(T)

其中|P|表示问题P的规模；n0为一阈值，表示当问题P的规模不超过n0时，问题已容易直接接触，不必再继续分解。(ADHOC(P)时该分治法中的基本子算法，用于直接解小规模的问题P。因此，当P的规模不超过n0时直接用算法(ADHOC(P)求解。算法 MERGE(y1,y2,...,yk)时该分治发中的合并子算法，用于将P的子问题P1,P2,...,Pk的相应的解y1,y2,...,yk合并为P的解。

分治算法最佳实践----汉诺塔

汉诺塔的传说

       汉诺塔又称河内塔问题时源于硬度一个古老传说的益智玩具。大梵天创造直接的时候做了三个金刚石主子，在一根柱子上从上往下按照大小顺序摞着64片黄金圆盘。大梵天命令婆罗门把圆盘从下面按照大小顺序重新摆放再另一根柱子上。并且规定，再小圆盘上不能放大圆盘，在三根柱子之间一次只能移动一个圆盘。

       假如每秒钟一次，共需多长时间呢？移玩这些金属片需要5845.54亿年以上，太阳系的语气寿命据说也就是数百亿年。真的过了5845.54亿年，地球上的一切生命早已灰飞烟灭。

汉诺塔游戏的思路分析：

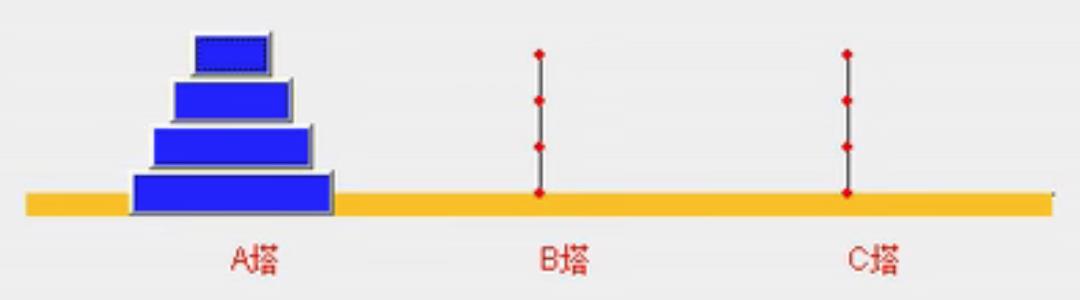
（1）如果是有一个盘，A->C。如果我们有n>=2情况，我们总是可以看做是两个盘1.最下面的盘 2.最上面的盘

（2）先把最上面的盘A->B

（3）把最下边的盘A->C

（4）把B塔的所有盘从B->C

2.详细内容

namespace MyAlgorithm.DAC

    /// <summary>
    /// DAC----分治（Divide-and-conquer(P)）
    /// Hanoitower ---- 汉诺塔
    /// </summary>
    public class Hanoitower
    
        public static void Move(int num, char a, char b, char c) 
        
            //如果只有一个盘
            if (num == 1)
            
                Console.WriteLine($"第1个盘从a -> c");
            
            else
            
                //如果我们有n>=2情况，我们总是可以看做是两个盘1.最下面的盘 2.最上面的盘
                //1.先把最上面的盘A->B，移动过程会使用到C
                Move(num - 1, a, c, b);
                //2.把最下边的盘A->C
                Console.WriteLine($"第num个盘从a -> c");
                //3.把B塔的所有盘从B->C，移动过程会使用到A
                Move(num - 1, b, a, c);
            
        
    

internal class Program
    
        static void Main(string[] args)
        
            Hanoitower.Move(5,'A', 'B', 'C');
            Console.Read();