pulp求解简单线性规划问题

Posted 2022-09-14 Icy Hunter

文章目录

• pulp
• • 非整数约束
  • 整数型约束
  • 求解状态的一些解释
  • 例题1
  • 例题2
• 参考

pulp

PULP是一个线性规划(Linear Programming, LP)问题求解库。它将优化问题描述为数学模型，生成MPS或者LP文件，然后调用LP求解器，如CBC、GLPK、CPLEX、Gurobi等来进行求解。

安装完pulp库默认就拥有了CBC求解器，其他求解器需要额外安装才能使用。

pip install pulp

即可

看一个例题即可：

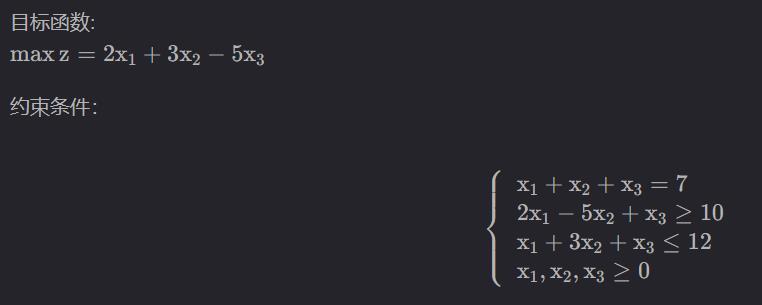
非整数约束

from pulp import LpVariable, LpMaximize, LpProblem, value, LpStatus

# 第一个参数为这个问题取名字，第二个参数表示求目标函数的最大值（LpMinimize）
prob = LpProblem('max_z', sense=LpMaximize)
# name为变量名， lowBound为下边界，None为没边界
x1 = LpVariable(name='x1', lowBound=0, upBound=None)
x2 = LpVariable('x2', 0, None)
x3 = LpVariable('x3', 0, None)

# 设置目标函数
prob += 2*x1+3*x2-5*x3
# 约束条件
prob += x1+x2+x3 == 7
prob += 2*x1-5*x2+x3 >= 10
prob += x1+3*x2+x3 <= 12

status = prob.solve()
print("求解状态:", LpStatus[prob.status])
print(f"目标函数的最大值z=value(prob.objective)，此时目标函数的决策变量为:",
      v.name: v.varValue for v in prob.variables())

输出：

整数型约束

from pulp import LpVariable, LpMaximize, LpProblem, value, LpStatus, LpInteger

# 第一个参数为这个问题取名字，第二个参数表示求目标函数的最大值（LpMinimize）
prob = LpProblem('max_z', sense=LpMaximize)
# name为变量名， lowBound为下边界，None为没边界, cat约束变量的类型LpInteger为整型
x1 = LpVariable(name='x1', lowBound=0, upBound=None, cat=LpInteger)
x2 = LpVariable('x2', 0, None)
x3 = LpVariable('x3', 0, None)

# 设置目标函数
prob += 2*x1+3*x2-5*x3
# 约束条件
prob += x1+x2+x3 == 7
prob += 2*x1-5*x2+x3 >= 10
prob += x1+3*x2+x3 <= 12

status = prob.solve()
print("求解状态:", LpStatus[prob.status])
print(f"目标函数的最大值z=value(prob.objective)，此时目标函数的决策变量为:",
      v.name: v.varValue for v in prob.variables())

输出：

求解状态的一些解释

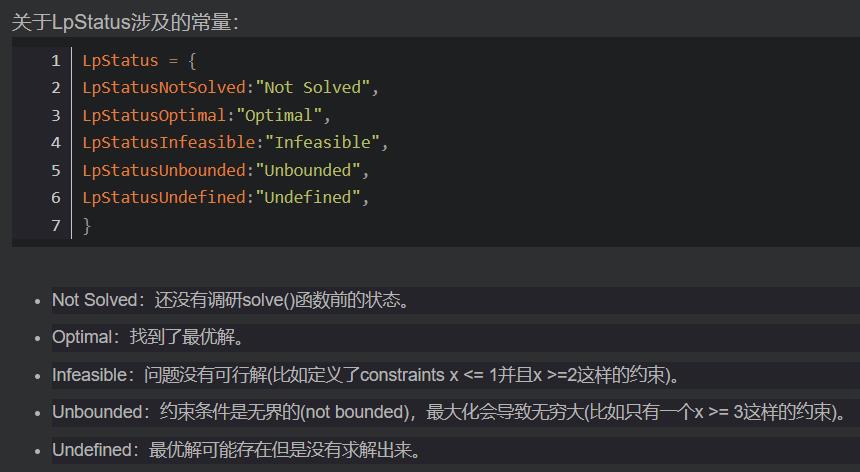
为了做作业求解才用了这个库，目前感觉还不错，挺方便的，摆两道题目。

例题1

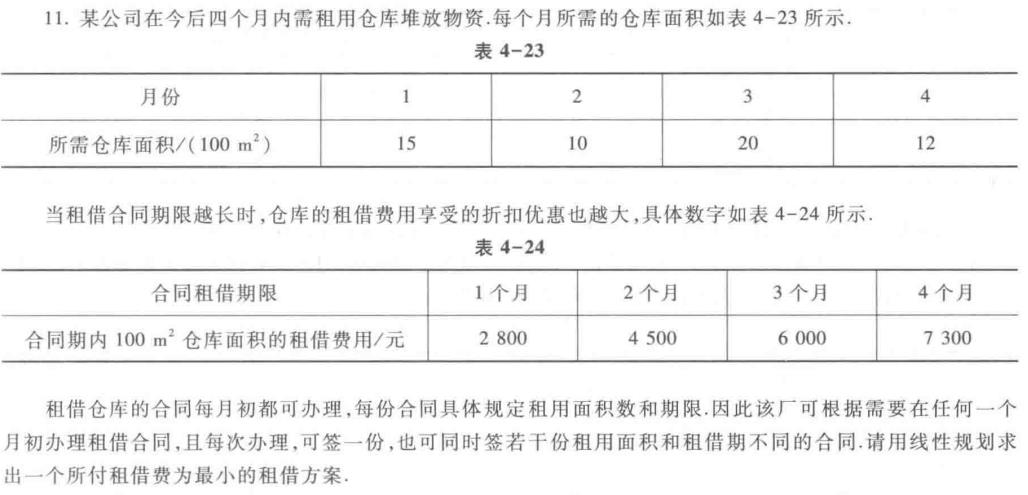
我们只需要设第i个月连租j个月的仓库为xij即可（i=1,2,3,4,j=1,2,3,4），不过值得注意的是，这里x24,x34这种应该不会存在，因为浪费了，因此需要设置的参数就少了。

from pulp import LpVariable, LpMaximize, LpProblem, value, LpStatus, LpInteger, LpMinimize

# 第一个参数为这个问题取名字，第二个参数表示求目标函数的最大值（LpMinimize）
prob = LpProblem('min', sense=LpMinimize)
# name为变量名， lowBound为下边界，None为没边界, cat约束变量的类型LpInteger为整型]
x = [[0]] 
for i in range(1, 5, 1):
    tmp = [0]
    for j in range(1, 5-i+1, 1):
        tmp.append(LpVariable(name='x'+str(i)+str(j), lowBound=0, upBound=None, cat=LpInteger))
    x.append(tmp)


# # 约束条件
prob += 2800*(x[1][1] + x[2][1] + x[3][1] + x[4][1]) + 4500*(x[1][2] + x[2][2] + x[3][2]) + 6000*(x[1][3] + x[2][3]) + 7300 * x[1][4]
prob += x[1][1] + x[1][2] + x[1][3] + x[1][4] >= 15
prob += x[1][2] + x[1][3] + x[1][4] + x[2][1] + x[2][2] + x[2][3] >= 10
prob += x[1][3] + x[1][4] + x[2][2] + x[2][3] + x[3][1] + x[3][2] >= 20
prob += x[1][4] + x[2][3] + x[3][2] + x[4][1] >= 12

status = prob.solve()
print("求解状态:", LpStatus[prob.status])
print(f"目标函数的最小值z=value(prob.objective)，此时目标函数的决策变量为:",
      v.name: v.varValue for v in prob.variables())

我这变量x自己操作了一下让索引从1开始，方便我列式子和打公式

输入目标函数或者约束条件时，不要换行，不然好像算不对。

输出结果：

计算出了最优解，看了一眼答案，算的是对的。

例题2

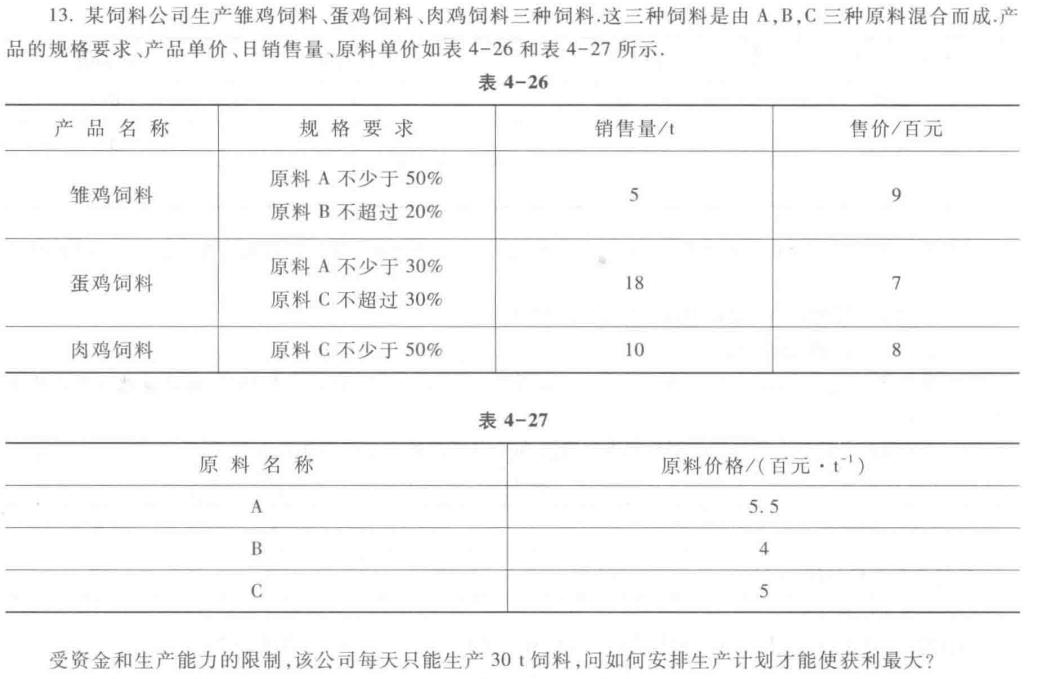
只需要设置第i种饲料需要第j种原料的数量为xij即可（i=1,2,3;j=1,2,3）。

那么求解如下：

from pulp import LpVariable, LpMaximize, LpProblem, value, LpStatus, LpInteger, LpMinimize

# 第一个参数为这个问题取名字，第二个参数表示求目标函数的最大值（LpMinimize）
prob = LpProblem('min', sense=LpMaximize)
# name为变量名， lowBound为下边界，None为没边界, cat约束变量的类型LpInteger为整型]
x = [[0]] 
for i in range(1, 4, 1):
    tmp = [0]
    for j in range(1, 4, 1):
        tmp.append(LpVariable(name='x'+str(i)+str(j), lowBound=0, upBound=None))
    x.append(tmp)

print(x)
# # 约束条件
prob += 9*(x[1][1] + x[1][2] + x[1][3]) + 7*(x[2][1] + x[2][2] + x[2][3]) + 8*(x[3][1] + x[3][2] + x[3][3]) - 5.5*(x[1][1] + x[2][1] + x[3][1]) - 4*(x[1][2] + x[2][2] + x[3][2]) - 5*(x[1][3] + x[2][3] + x[3][3])

prob += x[1][1] >= 0.5*(x[1][1] + x[1][2] + x[1][3])
prob += x[1][2] <= 0.2*(x[1][1] + x[1][2] + x[1][3])
prob += x[2][1] >= 0.3*(x[2][1] + x[2][2] + x[2][3])
prob += x[2][3] <= 0.3*(x[2][1] + x[2][2] + x[2][3])
prob += x[3][3] >= 0.5*(x[3][1] + x[3][2] + x[3][3])
prob += x[1][1] + x[1][2] + x[1][3] <= 5
prob += x[2][1] + x[2][2] + x[2][3] <= 18
prob += x[3][1] + x[3][2] + x[3][3] <= 10
prob += x[1][1] + x[1][2] + x[1][3] + x[2][1] + x[2][2] + x[2][3] + x[3][1] + x[3][2] + x[3][3] <= 30

status = prob.solve()
print("求解状态:", LpStatus[prob.status])
print(f"目标函数的最大值z=value(prob.objective)，此时目标函数的决策变量为:",
      v.name: v.varValue for v in prob.variables())

输出结果：

93百元，和答案一样。

参考

使用Python进行线性规划求解，高端操作亮瞎你的双眼（文末技术彩蛋）

管理运筹学——韩伯棠