基于内外环PD控制的四旋翼飞行器控制系统simulink仿真
Posted fpga和matlab
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了基于内外环PD控制的四旋翼飞行器控制系统simulink仿真相关的知识,希望对你有一定的参考价值。
目录
一、理论基础
1.1 四旋翼飞行器的动力学建模
四旋翼飞行器由于其飞行动力来自四个相互独立的电机,因此四旋翼飞行器也被称为四轴飞行器。通过四个电机可以快速实现四旋翼飞行器的起降,任意高度的控制悬停,翻滚飞行以及小曲率转弯等飞行功能。图2-1给出了四旋翼飞行器的实物图和数学模型简化图。
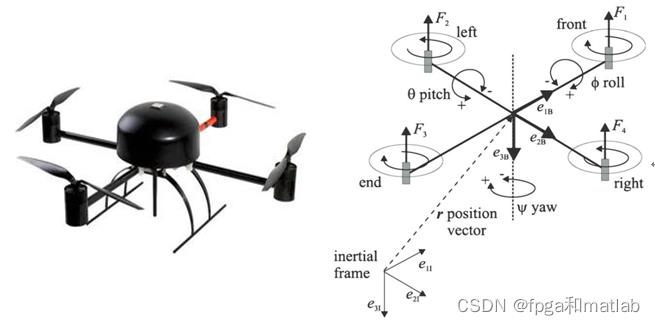
从图的结构示意图可知,四旋翼飞行器的四个电机为十字型等间隔分布。其中第一个电机和第三个电机选择方向为顺时针旋转,第二个电机和第四个电机选择方向为逆时针旋转。通过这四个电机可以给四旋翼飞行器产生四个上升动力,此外也可以通过改变四个电机的旋转速度,使得无人机产生各种不同的飞行动作。如果要保证四旋翼飞行器的飞行状态为悬停状态,那么只要保证四个电机的选择速度相同,且保证四个电机产生的动力和飞行器自身的重力相同就可以实现;如果四个电机产生的动力大于飞行器自身的重量,那么飞行器将上升;如果四个电机产生的动力小于飞行器自身的重量,那么飞行器将下降。如果其中2个电机产生的动力较大,2个电机产生的动力较小,那么飞行器将出现角度切斜的飞行状态。表2-1给出了四旋翼飞行器的飞行控制状态。
由地面坐标系到机体坐标系之间的转换计算公式:

无人机在这三个角度上的旋转矩阵分别可以表示为:
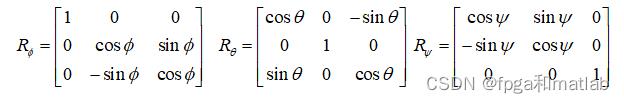
设变量U1为四旋翼飞行器的上升力;设变量U2为无人机的力矩;设变量U3为四旋翼飞行器的俯仰姿态的力矩;设变量U4表示的是四旋翼飞行器偏航姿态的反扭力矩。那么其动力学模型可以表示为:
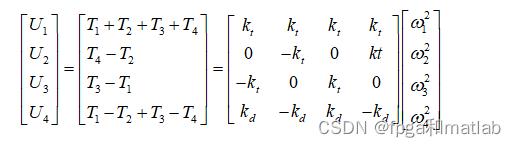
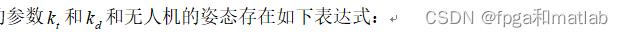
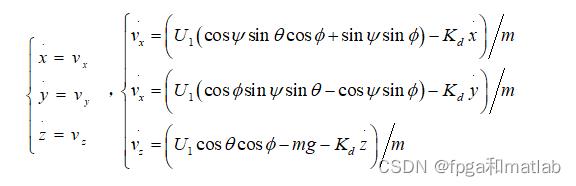
1.2 基于内外环的四旋翼飞行器的PD控制算法
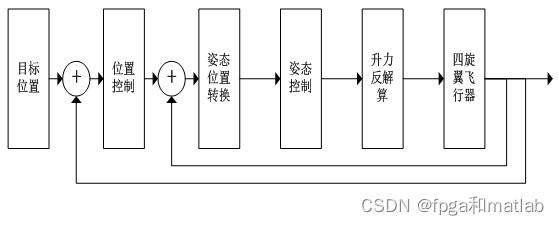
下面对该控制系统的基本原理和实现方式进行介绍,基于内外环的四旋翼飞行器的PD控制的基本结构如下图所示:

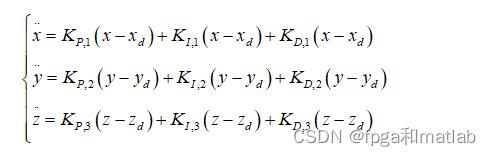
二、Simulink建模
在SIMULINK中建立如下的四旋翼飞行器的仿真模型:
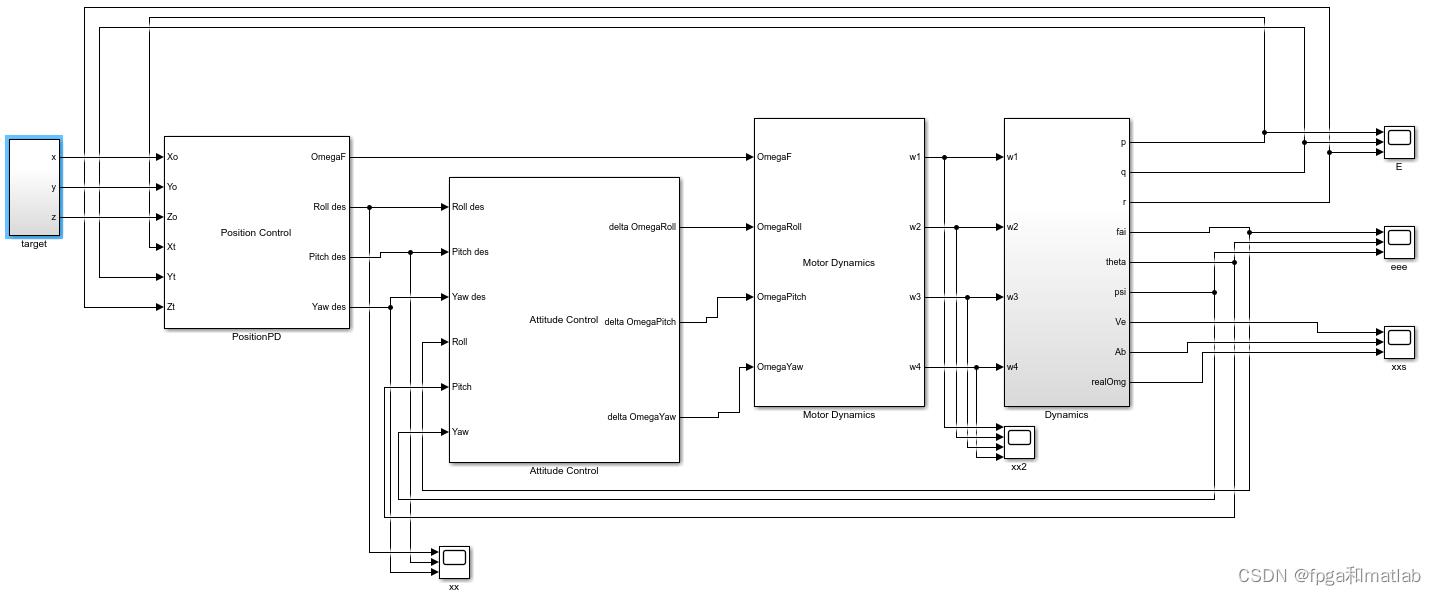
无人机模型主要包括位置控制模块姿态控制模块以及四旋翼飞行器动力学模型。下面对这些模型的建模实现方式进行介绍。
四旋翼飞行器的位置控制模块主要是由3个外环PD控制器组成,根据公式3.2我们构建如下的SIMULINK仿真模型:
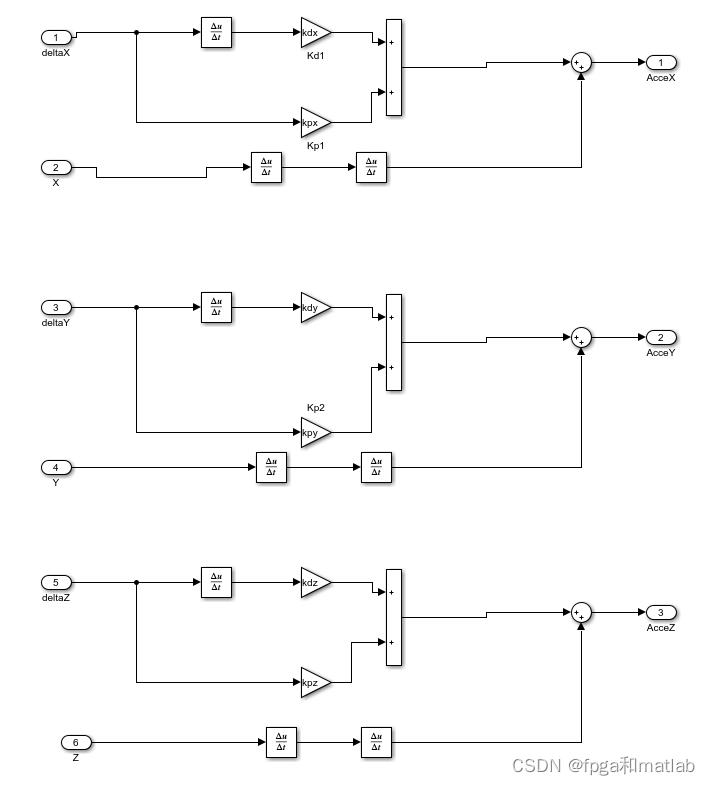
从图可知,通过三个PD控制器分别实现对四旋翼飞行器位置x,位置y以及位置z的控制,保证飞行器可以飞向预设的目标点位置。
姿态控制模块主要通过PD控制器实现对四旋翼飞行器的姿态控制,即,分别表示无人机的横滚角,俯仰角以及偏航角。通过PD控制器将横滚角的输出范围保持在-180~180之间,俯仰角的输出范围保持在-90~90之间,偏航角的输出范围保持在-180~180度之间。SIMULINK模型如下所示:
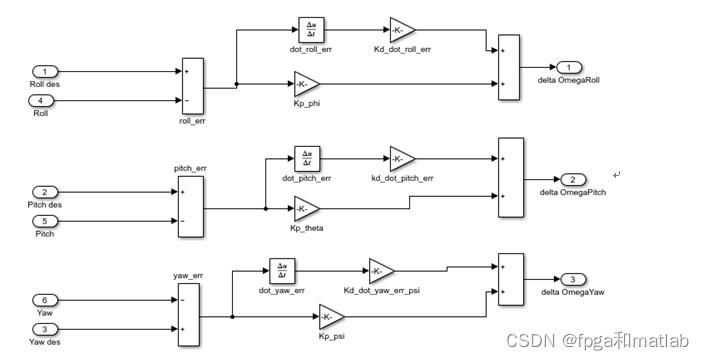
从该控制器的仿真模型可知,其主要通过一个比例参数和微分参数实现四旋翼飞行器的姿态控制,保证飞行器保持一个平稳的状态进行分析。
在6DOF (Euler Angles)模型中,通过设置四旋翼飞行器的初始坐标位置(Xe、Ye、Ze),初始速度(Vx、Vy、Vz),初始姿态(),四旋翼飞行器的质量参数以及初始的转动惯量(Ix、Iy、Iz)完成飞行器的配置,无人机固定坐标系的原点是无人机的重心。其参数设置界面如下图所示。
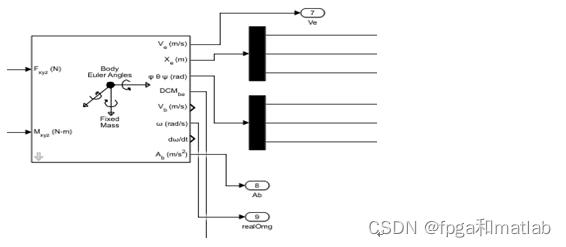
通过上述过程,实现了四旋翼飞行器的SIMULINK建模,下面将通过MATLAB/SIMULINK对该模型进行仿真分析。
三、仿真结果
对四旋翼无人机的横滚角以及俯仰角进行仿真,仿真结果如下所示:
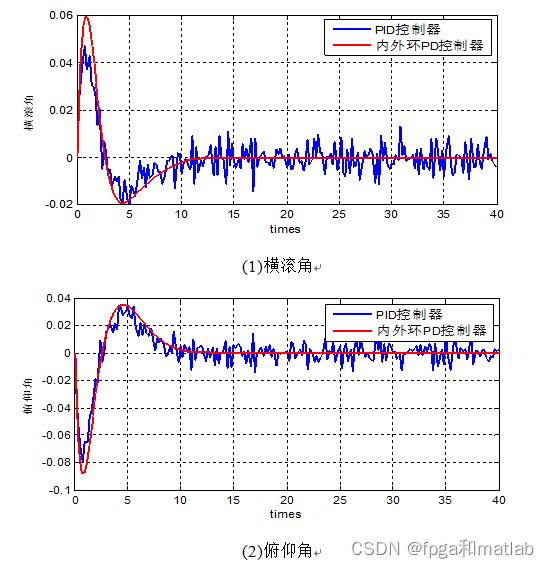
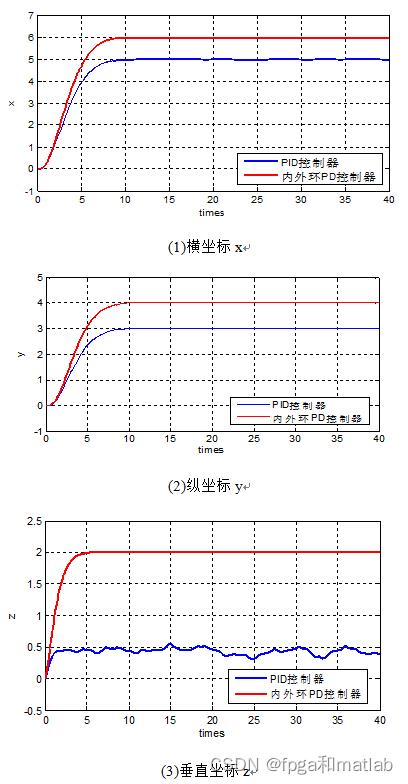
对四旋翼无人机的位置坐标控制进行仿真,仿真结果如下所示:
A08-81
以上是关于基于内外环PD控制的四旋翼飞行器控制系统simulink仿真的主要内容,如果未能解决你的问题,请参考以下文章