基于ODBTC有序抖动块截断编码和DCT域数字水印嵌入提取算法matlab仿真
Posted fpga和matlab
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了基于ODBTC有序抖动块截断编码和DCT域数字水印嵌入提取算法matlab仿真相关的知识,希望对你有一定的参考价值。
目录
一、理论基础
图像信息作为计算机上一个最重要的资源,对其有效的进行图像压缩处理无疑会给人们带来巨大的好处。但传统的图像块截断编码(block truncation coding,BTC)虽是一种极低复杂度的编码算法,但是当图像分块较大的时候,BTC编码算法会存在较为明显的块效应,且压缩效果较差等缺陷。针对这个问题提出了一种有序抖动块截断编码(Order dither block truncation coding,ODBTC),该算法不仅具有BTC编码算法的低复杂度特性,而且通过抖动矩阵来有效改善图像的压缩质量。在ODBTC图像压缩编码的基础之上提出一种基于位平面的DCT域数字水印嵌入提取算法,该算法在嵌入水印之前,首先将水印图像进行位平面分解,然后在ODBTC编码之后图像位平面进行DCT域的水印嵌入,并对嵌入水印后的位平面进行DCT逆变换,从而获得获得水印嵌入的效果,最后通过解码,得到嵌入水印的宿主图像。
1.1 有序抖动块截断编码
BTC编解码的整体流程图如下所示:
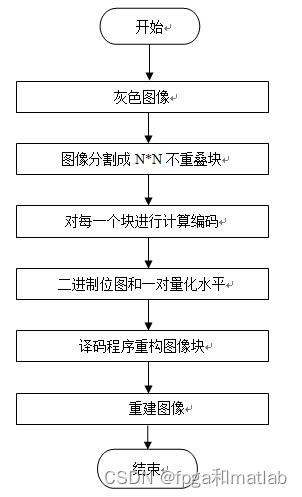

1.2 水印嵌入和提取
基于ODBTC编码后的DCT域图像位平面分解的水印嵌入算法流程图如下图所示:
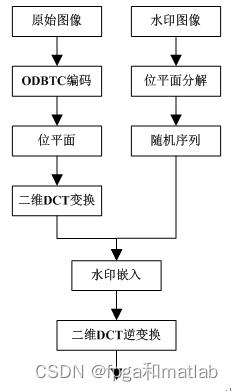
步骤1、根据本文第三章节所介绍的原理进行图像的ODBTC编码处理;
步骤2、对水印图像进行处理,获得其相应的位平面,将原始的水印图像转换为8个位平面图像。图像的位平面可以通过如下的示意图标示:
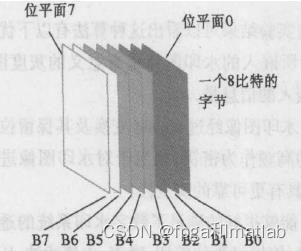
从图4.1可知,对水印信息计算其位平面,通过处理之后,将一个水印图像转换为8个位平面。一幅数字图像的每一个像素都是以多比特的方式存在的,而每一个像素通常为8位(像素值0到255)。所谓位平面的含义便是将每一个像素值都分解为8个位宽的二进制值,所有同权值的位构成的平面称为一个位平面。
步骤3、对图像ODBTC编码之后的图像位平面进行二维分块DCT变换。
步骤4、对二维分块DCT变换后的水印图像进行基于随机序列水印嵌入操作,具体处理公式如下所示:

公式4.1中,变量w表示的是水印图像;变量f表示的是原始DCT域图像;变量f'表示的是嵌入水印后的DCT域图像。
步骤5、进行二维DCT逆变换,获得嵌入水印后的图像;
水印嵌入之后,则进行水印的提取操作。基于ODBTC编码后的DCT域图像位平面分解的水印提取算法流程图如下图所示:

根据该流程图,水印提取算法的详细步骤如下:
步骤1、对图像进行DCT变换,获得DCT域的嵌入水印图像;
步骤2、产生和嵌入水印相同的随机序列。由于水印在嵌入的时候,是根据随机序列的极性进行水印的嵌入。因此,我们在水印提取的时候,充分考虑了这个特性。
步骤3、将DCT变换后的嵌入水印图像和随机序列做相关运算,从而获得水印信息的嵌入位置和水印信息。该步骤是水印提取的核心步骤,其主要利用了随机序列的相关特性来实现的。
首先,随机序列具有四大特性,分别为随机序列中高低电平出现的次数大致相等;随机序列具有良好的相关特性;随机序列中连续出现的高电平或低电平被称为游程,而长度为n(n为自然数)的游程出现的次数占总游程数的1/2;随机随意将一个序列位移得到的新序列与原序列比较,只有一半的元素相同。
然后,通过随机序列的自相关运算:
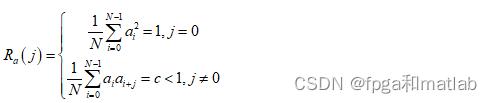
由于这里采用的是伪随机序列,因此其属于一种周期函数,因此自相关函数也是周期函数,它是以周期N重复的。
二、MATLAB程序
clc;
clear;
close all;
warning off;
%输入水印图片
Imark = rgb2gray(imread('黑白水印.jpg'))/255;
%Imark = imread('1.bmp');
[file,path] = uigetfile('*.bmp');
X = imread([path,file]);
X = imresize(X,[384,384]);
block_size = 4;
X1 = double(X);
[n,m] = size(X);
binary = zeros(n,m);
low_high = zeros(n*m/(block_size^2),2);%存放每个像素块low mean(第一列) 和high mean(第二列)
DAblock_size=bayer_dither(block_size);
for i=1:block_size:n
for j=1:block_size:m
temp=X1(i:i+block_size-1,j:j+block_size-1);
Bmax=max(max(temp));
Bmin=min(min(temp));
k=Bmax-Bmin;
DAk=DAblock_size.*(k/(block_size^2-1));
Th=DAk+Bmin;
Xbinary=(temp>=Th);
n1=ceil(i/block_size);
m1=ceil(j/block_size);
low_high((n1-1)*(m/block_size)+m1,1)=Bmin;
low_high((n1-1)*(m/block_size)+m1,2)=Bmax;
binary(i:i+block_size-1,j:j+block_size-1)=Xbinary;
end
end
%在编码后的位平面中嵌入水印信息
%设置嵌入强度
Power = 800;
%设置块的大小
RR = 45;
CC = 45;
Mwk_binary= func_insert(binary,Imark,Power,RR,CC);
figure;
subplot(121);
imshow(imread('黑白水印.jpg'));
title('嵌入的水印图像');
subplot(122);
imshow(X);
title('未嵌入水印的图像');
%
% subplot(223);
% imshow(binary);
% title('图像编码后的位平面');
%
% subplot(224);
% imshow(Mwk_binary);
% title('嵌入水印后的位平面');
save btc_image.mat binary Mwk_binary Power RR CC
save low_high.mat low_high;
clc;
clear;
close all;
warning off;
tic;
load btc_image.mat;
load low_high.mat;
[Imark,Mwk_binarys] = func_desert(Mwk_binary,RR,CC,4);
figure;
subplot(122);
imshow(Imark,[]);
title('提取水印');
binary = Mwk_binarys;
[n,m] = size(binary);
[l,h] = size(low_high);
gray = zeros(n,m);
block_size =(n*m/l)^0.5;
for i=1:block_size:n
for j=1:block_size:m
n1=ceil(i/block_size);
m1=ceil(j/block_size);
a=low_high((n1-1)*(m/block_size)+m1,1);
b=low_high((n1-1)*(m/block_size)+m1,2);
temp=binary(i:i+block_size-1,j:j+block_size-1);
temp1=temp;
dix= temp==0;
temp1(dix)=a;
dix=find(temp==1);
temp1(dix)=b;
gray(i:i+block_size-1,j:j+block_size-1)=temp1;
end
end
subplot(121);
imshow(uint8(gray));
title('解码后的图像');
toc;
%提取水印的性能分析
Imark0 = imread('1.bmp');
%以下是根据参考文献《基于位平面分解的数字水印算法》公式3,公式4
Imark0=imresize(Imark0,[45,45]);
PSNR = func_psnr((Imark0),(Imark))
NC = func_nc((Imark0),(Imark))
三、仿真结果
首先,水印提取之后的结果如下所示:

对提取的水印进行计算PSNR和NC指标,分别为:
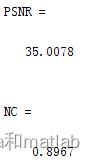
然后对于算法进行噪声共计,测试系统的稳定性。
做噪声攻击,获得如下的仿真结果:

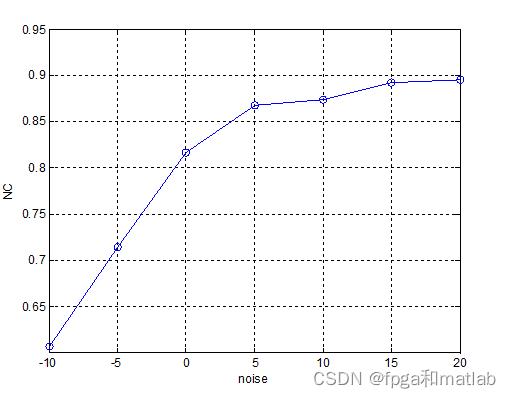
从噪声攻击来看,当噪声大小大于0db的时候,算法基本可以获得较为稳定的水印提取效果。
第二,做旋转攻击,即对图像进行小角度的倾斜旋转,然后进行水印提取,仿真结果如下:

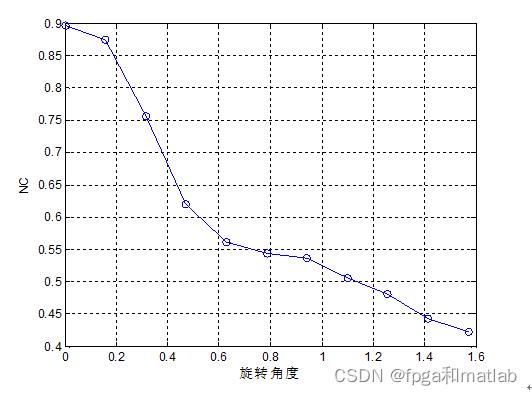
这里,旋转角度从0到90度进行测试,通过仿真结果可知,当旋转角度大于36度的时候,水印提取质量快速下降。
但在实际中,图像的倾斜角度一般都是10度以内的,所以该算法具备一定的抗旋转能量。
最后对图像的压缩比进行攻击测试:
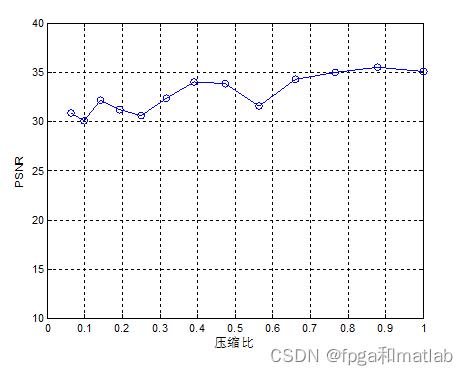

分别进行压缩图像,压缩大小为12.5%,25%,50%,100%。获得如上的仿真结果,从仿真效果可知,算法对压缩攻击具有较强的抗干扰能力
A11-04
以上是关于基于ODBTC有序抖动块截断编码和DCT域数字水印嵌入提取算法matlab仿真的主要内容,如果未能解决你的问题,请参考以下文章