[LeetCode]剑指 Offer 07. 重建二叉树

Posted 2022-09-06 Spring-_-Bear

输入某二叉树的前序遍历和中序遍历的结果，请构建该二叉树并返回其根节点。

假设输入的前序遍历和中序遍历的结果中都不含重复的数字。

示例 1:

   3
  / \\
  9 20
    / \\
   15  7

Input: preorder = [3,9,20,15,7], inorder = [9,3,15,20,7]
Output: [3,9,20,null,null,15,7]

示例 2:

Input: preorder = [-1], inorder = [-1]
Output: [-1]

限制：

• 0 <= 节点个数 <= 5000

题解：

• 前序遍历：[根节点 | 左子树 | 右子树]
• 中序遍历：[左子树 | 根节点 | 右子树]
• 后序遍历：[左子树 | 右子树 | 根节点]

以下解法只适用于树中无重复节点值的情况

1. 前序遍历的首元素必定为树的根节点 node 的值
2. 在中序遍历中搜索根节点 node 的索引 ，可将中序遍历划分为 [ 左子树 | 根节点 | 右子树 ]
3. 根据中序遍历中的左（右）子树的节点数量，可将前序遍历划分为 [ 根节点 | 左子树 | 右子树 ]

例如以题目示例为例：

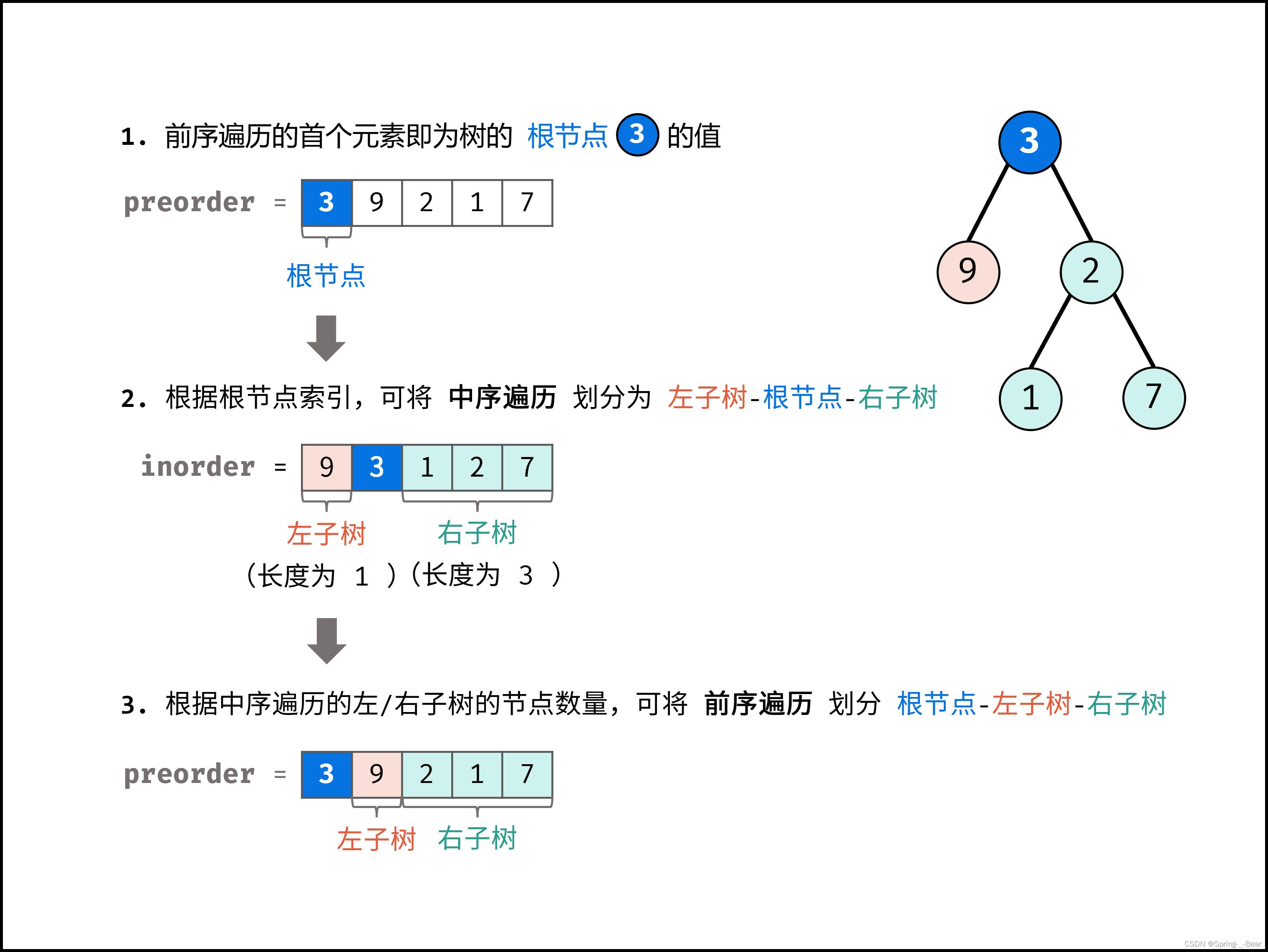
通过以上三步，可确定树的根节点、左子树根节点、右子树根节点，

根据「分治算法」思想，对于树的左、右子树，仍可复用以上方法划分子树的左右子树。

分治算法解析：

• 递推参数：根节点在前序遍历的索引 root 、子树在中序遍历的左边界 left 、子树在中序遍历的右边界 right
• 终止条件： 当 left > right ，代表已经越过叶节点，此时返回 null
• 递推工作：

  1. 建立根节点 node ：节点值为 preorder[root]

  2. 划分左右子树：查找根节点在中序遍历 inorder 中的索引 i

  3. 构建左右子树： 开启左右子树递归

     	根节点索引	中序遍历左边界	中序遍历右边界
     左子树	root + 1	left	i - 1
     右子树	i - left + root + 1	i + 1	right

  4. 返回值： 回溯返回 node ，作为上一层递归中根节点的左 / 右子节点

class Solution 
    int[] preorder;
    Map<Integer, Integer> dic = new HashMap<>();

    /**
     * 剑指 Offer 07. 重建二叉树
     *
     * @param preorder 先序遍历
     * @param inorder  中序遍历
     */
    public TreeNode buildTree(int[] preorder, int[] inorder) 
        this.preorder = preorder;
        // 将中序遍历的元素放进 Map 中，方便查找
        for (int i = 0; i < inorder.length; i++) 
            dic.put(inorder[i], i);
        
        return recur(0, 0, inorder.length - 1);
    

    /**
     * 二叉树重建
     *
     * @param root  根节点在前序遍历的索引
     * @param left  子树在中序遍历的左边界
     * @param right 子树在中序遍历的右边界
     */
    private TreeNode recur(int root, int left, int right) 
        // 递归终止
        if (left > right) 
            return null;
        
        // 建立根节点
        TreeNode node = new TreeNode(preorder[root]);
        // 依据根节点在中序遍历中的位置划分根节点、左子树、右子树
        int i = dic.get(preorder[root]);
        // 开启左子树递归
        node.left = recur(root + 1, left, i - 1);
        // 开启右子树递归
        node.right = recur(root + i - left + 1, i + 1, right);
        return node;
    

来源：力扣（LeetCode）
链接：https://leetcode.cn/problems/zhong-jian-er-cha-shu-lcof