重温基础算法内部排序之插入排序法

Posted 2022-09-06 顧棟

内部排序之插入排序法

文章目录

• 内部排序之插入排序法
• • 主要思想
  • 过程演示
  • JAVA代码
  • 算法分析

主要思想

插入排序(InsertionSort)，一般也被称为直接插入排序。

将一个记录插入到已排好序的序列中，从而得到一个新的有序序列（序列的第一个数据，应直接插入看成是一个有序的子序列，然后从第二个记录逐个向该有序的子序列进行有序的插入，直至整个序列有序）

过程演示

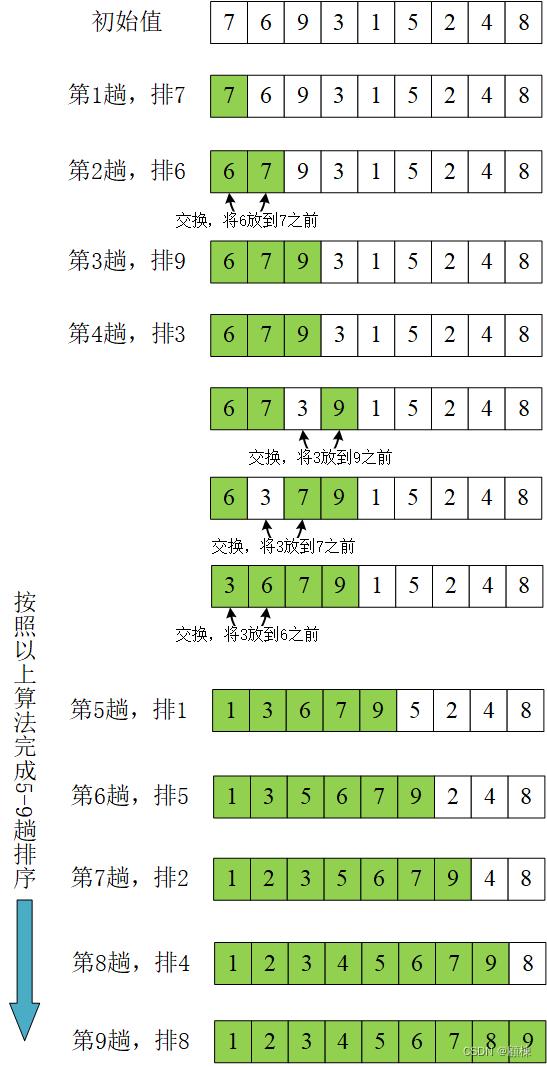
JAVA代码

package sort;

/**
 * 插入排序
 *
 * @author Donny
 * @date 2022/9/2
 */
public class InsertionSort 

    public static void main(String[] args) 
        int[] o = 7, 6, 9, 3, 1, 5, 2, 4, 8;

        System.out.print("排序前: ");
        for (int t : o) 
            System.out.print(t);
            System.out.print(" ");
        
        System.out.println();

        // 算法部分
        // step 1
        for (int i = 1; i < o.length; i++) 
            // step 2
            int temp = o[i];
            // step 3
            for (int j = i; j > 0; j--) 
                // step 4
                if (temp < o[j - 1]) 
                    // step 5
                    o[j] = o[j - 1];
                    // step 6
                    o[j - 1] = temp;
                 else 
                    // step 7
                    break;
                
            
        

        System.out.print("排序后: ");
        for (int t : o) 
            System.out.print(t);
            System.out.print(" ");
        
        System.out.println();
    

排序前: 7 6 9 3 1 5 2 4 8 
排序后: 1 2 3 4 5 6 7 8 9 

算法分析

当初始序列为正序时，只需要外循环n-1次，每次进行一次比较，无需移动元素。

比较次数$n-1$

移动次数=$0$

那么时间复杂度为$O(n)$。

当初始序列为反序时，需要外循环n次，每次排序中待插入的元素都要和[0,i-1]中的i个元素进行比较且要将这i个元素后移i次，加上temp = o[i]与o[j - 1] = temp的两次移动，每趟移动次数为i+2,此时比较次数和移动次数达到最大值。

比较次数=$1+2+...+（n-1）=n\ast (n-1)/2=O(n^2)$

移动次数=$(1+2)+(2+2)+(...)+(n-1+2)=(n-1)\ast (n+4)/2=O(n^2)$

即时间复杂度为$O(n^2)$。

空间复杂度 算法中只借助了i, j, temp三个变量，跟待排序的数组规模无关，所以为$O(1)$。