误码率仿真基于matlab LDPC编译码误码率仿真含Matlab源码 2079期
Posted 海神之光
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了误码率仿真基于matlab LDPC编译码误码率仿真含Matlab源码 2079期相关的知识,希望对你有一定的参考价值。
一、LDPC简介
1 LDPC码编码
LDPC码是一种性能非常接近香农极限的“好”码, 它是惟一用校验矩阵来表示的线性分组码。LDPC码的编码主要分两步进行, 首先构造奇偶校验矩阵, 然后是基于奇偶校验矩阵的编码算法。
1.1校验矩阵的构造
根据式子nj = mk可知, 规则的LDPC码 (n, j, k) , 当参数n, j, k确定后, 可以得到校验方程的数目m, 则校验矩阵H的大小就可以定为m × n。构造LDPC码校验矩阵的一般步骤为:先生成一个m行n列的全0矩阵, 然后随机地将每列中的j个0换成1, 每行中的k个0换成1。但在随机置l的过程中, 必须避免出现长度为4的环[4]。 如果最小环长为4, 在迭代中非常容易造成错误信息的扩散传播, 从而导致译码性能的下降[5]。
Mackay为了消除校验矩阵中长度为4的环, 基于Tanner图提出了改进的构造方案。采取的准则是:在构造时必须保证任意两列间的交叠重量不超过1。本文采用的是Mackay的1A构造方法, 按照此方法构造的一个LDPC码 (3, 6) 码如图1所示。
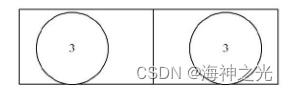
图1 Mackay的1A构造方法
Mackay的1A构造方法是最基本的一种构造方法, 它要求保证固定列重为 γ , 而行重尽可能均匀的保持为 ρ 。 利用Mackay构造方法得到的LDPC码距离特性很好, 且没有短环。
1.2基于奇偶校验矩阵的编码算法
LDPC码的直接编码方法就是利用高斯消去法, 产生一个下三角矩阵, 然后进一步初等变换得到右边单位阵形式H =[P|I] , 由G =[I|P] 得到生成矩阵, 再利用信息码元向量u和生成矩阵G相乘可得到完整码字C, 即C = M*G直接编码。
2 LDPC码译码
BP算法是在Gallager提出的概率译码算法基础上发展而来的。BP算法每次迭代包括2步:变量节点的处理和校验节点的处理。概率域就是在节点间传递的是概率信息, 采用很多乘法运算, 运算量大;而对数域的和积算法实现是将概率值通过对数似然比变化为软信息值 (LLR) , 再进行传递, 这样就将大量乘法运算变为加法运算, 大大简化了译码复杂度, 利于硬件实现。下面重点介绍对数域迭代APP LLR译码算法。
2.1迭代APP LLR译码算法的变量定义
对于 (N, K) LDPC码, 定义变量U取值为0和1时的对数似然比 (LLR) 为:

设发端发送的码字为u =[u1, u2, …, uN] , 接收码字为y =[y1, y2, …, yN] , 由此可以得出在迭代中传递的校验节点和信息节点的软信息为:
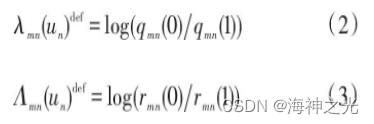
2.2迭代APP LLR译码算法
迭代APP LLR译码算法的迭代过程如下:
(1) 初始化:设每个变量节点n的软信息为:
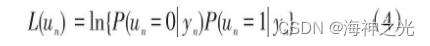
对于矩阵中H (m, n) = 1, 相应的变量节点的软信息初始化为信道输出的软信息, 即 λmn (un) = L (un) , Λmn (un) = 0。
(2) 校验节点更新:根据每个变量节点n, 向与该变量节点相连的所有校验节点传递更新的软信息, 计算校验节点信息:

(3) 变量节点更新:根据每个校验节点m, 向与该校验节点相连的所有变量节点传递更新的软信息:
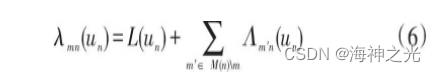
对变量节点n进行判决时, 变量节点软信息应为:
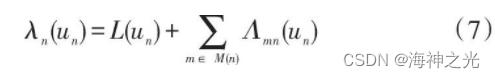
(4) 判决:当 λn (un) ≥0, 则ûn= 0 , 否则ûn= 1, 此时判决出的码为:û=u1, , û2, …, ûN。最后根据校验矩阵来判断所译出的码字是否正确。如果ûHT= 0, 那么译码正确, 此时, 停止迭代;否则继续迭代进行译码, 直到迭代次数达到所设定的最大次数。如果此时仍未正确译码, 则译码失败。
由以上所述可见, 在变量节点更新时只有加法运算, 但是还可以再进一步降低算法的实现复杂度。采用迭代APP LLR算法, 将LLR BP算法中的 λn (un) 代替λmn′ (un′) 参与校验信息的迭代。即 λn (un) 不仅用于硬判决, 还用于校验信息的更新。这样所传递的变量消息之间便引进了相关性, 传递的变量消息就不再是外部消息, 仅仅需要计算和存储一个变量消息的数值, 可以大大地降低算法的复杂度。
二、部分源代码
clear all;
clc;
%tic
rows=256;
cols=512;
count=20;
SNR=0:1:6;
for SNRindex=1:length(SNR)
total_err=0;
errmax=0;
nerr=0;
loop=0;
while loop<count
s=round(rand(1, cols-rows));%1*128的0,1矩阵
%产生H矩阵
H=genH(rows,cols);
%使用H矩阵进行LDPC编码
[u,P,rearranged_cols]=ldpc_encode(s,H);
%SNR=5;%信噪比
amp=1;%信号幅值
tx_waveform=bpsk(u,amp);
rx_waveform=awgn(tx_waveform,SNR(SNRindex));
scale(1:length(u))=1; %No fading.
%LDPC译码
[uhat vhat]=ldpc_decode(rx_waveform,SNR(SNRindex),amp,scale,H,rearranged_cols);
errmax=find(s~=uhat);
nerr=length(errmax);
total_err=total_err+nerr;
loop=loop+1;
%loop
end
errratio=total_err/(length(s)*count);
lerror(SNRindex)=errratio;
SNRindex
end
%errratio
%end
%figure(1);
semilogy(SNR,lerror,‘-bo’);
xlabel(‘信噪比/dB’)
ylabel(‘误码率’)
grid on
title(‘average BER’)
axis([0 6 10^-5 10^0])
legend(‘LDPC编码’)
%toc
三、运行结果
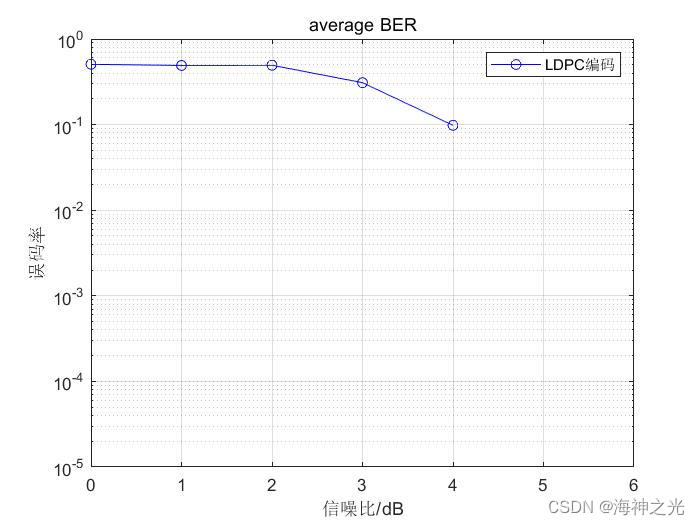
四、matlab版本及参考文献
1 matlab版本
2014a
2 参考文献
[1] 李秀花,高永安,马雯.LDPC码译码算法及性能分析[J].现代电子技术. 2014,37(01)
3 备注
简介此部分摘自互联网,仅供参考,若侵权,联系删除
以上是关于误码率仿真基于matlab LDPC编译码误码率仿真含Matlab源码 2079期的主要内容,如果未能解决你的问题,请参考以下文章
基于MATLAB的qc-ldpc编译码误码率仿真,译码算法对比最小和译码
RA-LDPC编译码和QC-LDPC编译码的误码率matlab仿真
MATLAB教程案例10使用MATLAB自带的LDPC工具箱实现LDPC编译码误码率仿真