图计算思维与实践 核心概念与算法
Posted Mr-Bruce
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了图计算思维与实践 核心概念与算法相关的知识,希望对你有一定的参考价值。
前言
在前文《图计算思维与实践 (一)概览》中,我们介绍了以知识图谱、网络分析为主的图计算的应用,阐述了图思维的方式。本文我们将进入第二部分:图相关的核心概念与算法,这些是进行图探索的基础。在本文的介绍中,我会避开一些数学相关的细节,尽可能从“是什么”、“在解决什么样的问题”的角度来阐述,让大家有个整体的认识。有了基本的认识,才有可能在实践中意识到可以用这些来解决问题,然后有针对性的去研究细节。

图概念
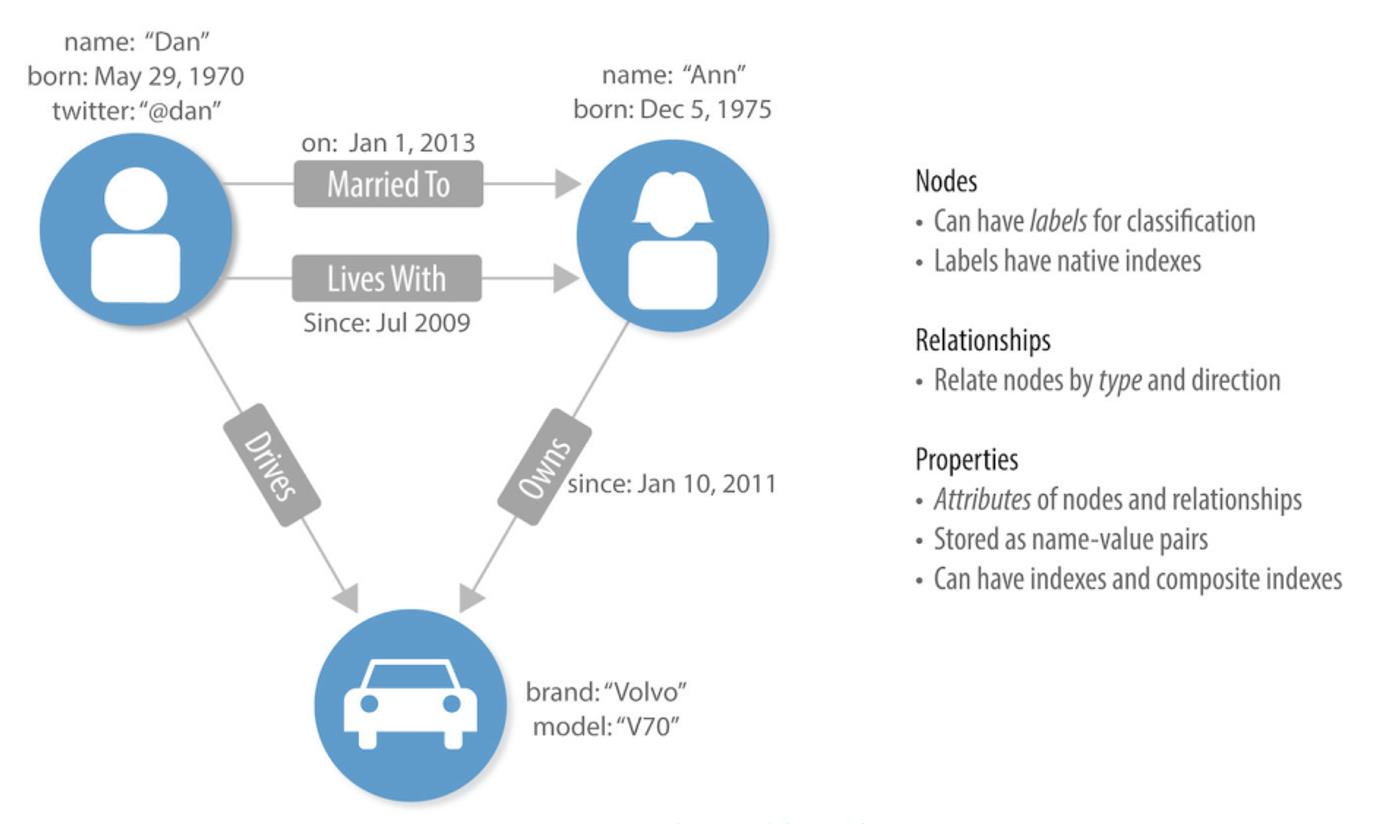
图是一种非常直观的描述现实的结构,其基本构成包含三部分:节点、节点之间的关系、附加在节点或关系上面的属性。节点通过标签可以划分成不同类型,关系通过类型和方向进行标识,属性用于对节点或关系的详情进行描述。以下图为例,图中有三个节点:两个人物和一辆汽车,在人物节点上有属性“姓名”、“出生时间”,在汽车节点上有属性“品牌”、“型号”;图中还有四种关系,关系上有属性“发生时间”。通过这个图,我们可以了解到:Dan出生于1970年5月29日,Ann出生于1975年12月5日,两人于2009年7月居住在一起,之后在2013年1月1日结婚;Ann在2011年1月10日购买了一辆Volvo V70汽车,之后Dan经常开这辆车。
同样的节点,通过不同的关系连接起来会呈现出不同特性的图,“不同的关系”包括关系的类型、方向、属性值的不同。比较常见的有下面四种特性:
- 无权图与有权图。取决于关系上是否有权值属性,比如在两个地点之间会有距离作为权值。
- 连通图与非连通图。如果任何两个节点之间都有一个路径可以连接起来,那么图就是连通的,否则为非连通。
- 无向图与有向图。取决于关系是否有方向,有方向的为有向图,否则为无向图。
- 无环图与有环图。如果从某个节点出发,能找到一条路径回到自己,那么图就是有环的,否则为无环。

这些图的基本概念与特性是进行深入探索的前提,很多算法都是基于此做出来的。同时,这些概念也被广泛应用在很多工程领域,比如DAG(有向无环图),常被用在任务调度相关的应用中。下图是两个应用DAG的开源框架:Spark和Airflow。Spark是一款基于内存的分布式并行计算框架,其会通过DAGScheduler来生成执行计划,确保任务的正常调度与执行;Airflow是一款任务依赖管理框架,其会检测我们编写的任务依赖关系,确保任务之间不会形成环路。

图算法
图的算法有很多,这里主要介绍三种最基本的算法:路径发现算法、中心性算法、社区发现算法。之所以说是“最基本”,是因为一方面它们是很多高级算法的底层基础,另一方面它们是我们拿到一个图进行探索时首先需要考虑、尝试的一些事情。这三种算法是大的分类,每一种里面都有很多具体的算法。
路径发现算法,用于探索节点之间的最佳路径,主要有下面5个方面,每个方面都有一些具体的算法。
- 最短路径。给定两个节点,找出二者之间的最短路径。
- 单源最短路径。给定一个节点,探索其到其他每个节点的所有最短路径。
- 全最短路径。探索每个节点到其他每个节点的所有最短路径。可以看到,从“最短路径”到“单源最短路径”再到“全最短路径”,是一个输入的递进关系,简单的话可以通过循环来解决,但是有更加优化的算法可以做的更有效率。
- 最小生成树。探索能将所有节点连接起来的最短路径。
- 随机游走。从某个节点出发,随机选择下一个节点,在整个图里面随机遍历,直到满足某个条件。

中心性算法,用于探索在图中具有影响力的节点,常见的有下面4个方面。
- 度中心性。最简单的一种中心性探索,看一个节点与其他节点的连接数量,数量越多表示影响力越大。根据实际需要,可能会区分入度与出度,入度指的是别的节点指向自己的连接数量,出度指的是自己指向别人的连接数量。
- 接近中心性。探索一个节点到其他所有节点的最短路径的总和,数值越小表示影响力越大。举例来说,如果想在一个城市开一个超市,那么超市到周边各个小区的交通用时越少,就表示越处于中心位置。
- 中介中心性。探索经过一个节点的最短路径的数量,数量越多表示影响力越大。举例来说,这样的节点,通常处于一个桥的位置,将不同的村庄连接起来。
- PageRank。PageRank是Google提出的用于解决网页排名的算法,基本思路是:一个网页被很多其他网页所链接,说明它受到普遍的承认和信赖,那么它的排名就高。因为这里使用了网页、网页的关系,所以同样的思路可以引入到图计算中,来判断某个节点的影响力,即PageRank的分值越高表示影响力越大。

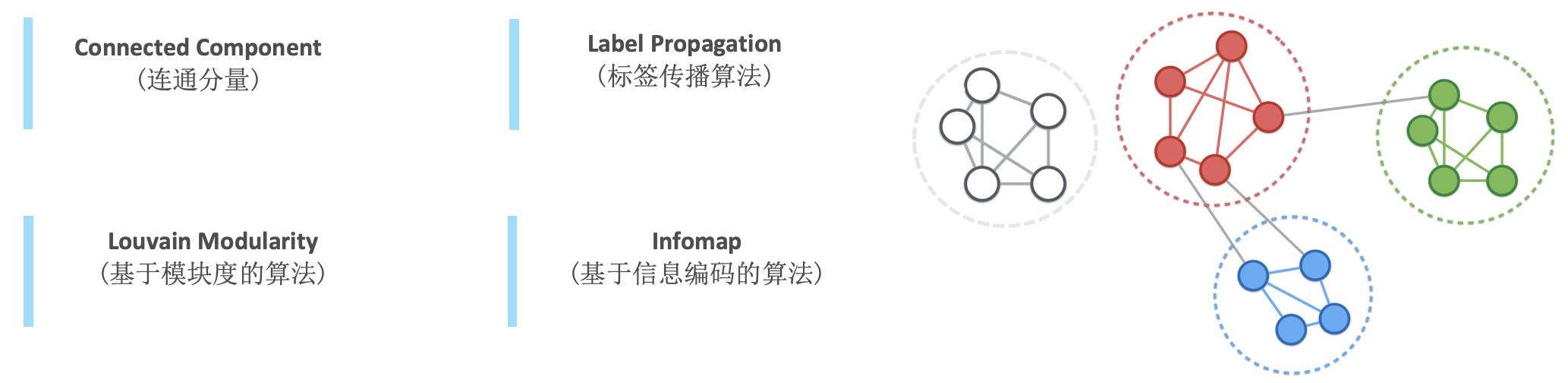
社区发现算法,用于探索图中具有紧密联系的群体。社区,指的是一个子图,这个子图内部各个节点之间的连接程度远远高于这些节点跟外部其他节点之间的连接。社区发现类似于机器学习里面的聚类,只是在聚类里面我们更加侧重于数据点的属性,而在社区发现中侧重于节点之间的关系。比较常见的有下面4种算法。
- 连通组件(Connected Component)。用于发现连通节点的集合,通常拿到一个图之后,我们首先便会看看它有多少个连通组件。以下图中右边的图为例,里面有两个连通组件。对于某个连通组件,如何进一步探索其内部有多少社区呢?这便是下面几个算法要解决的问题。
- 标签传播算法(Label Propagation)。基本思路是:
- 初始时,为每个节点分配一个标签;
- 每一次迭代都要计算新的标签,规则是:统计节点所有邻居的标签,出现次数最多的标签将被设置成这个节点的新标签,如果有多个就随机选择一个;
- 经过多次迭代,直到所有的节点都满足: 节点的标签是它的邻居标签中出现次数最多的(或最多的之一)。
- 基于模块度的算法(Louvain Modularity)。模块度是评估一个社区网络划分好坏的度量方法,物理含义是社区内节点的连边的权重之和与随机情况下的连边的权重之和的差距。基于模块度的算法,是以最大化模块度为目标。
- 基于信息编码的算法(Infomap)。Infomap设计之初想解决的问题是:如果在一张图上做随机游走(不限步数的游走),如何用最短的编码来描述随机游走产生的路径?Infomap的思路是采用双层结构,将不同节点划分群组(社区),在编码时候需要两种信息:群组和每个群组内部的节点。关于Infomap的详情,可以进一步阅读The map equation,本文下面截取了其中一张图。
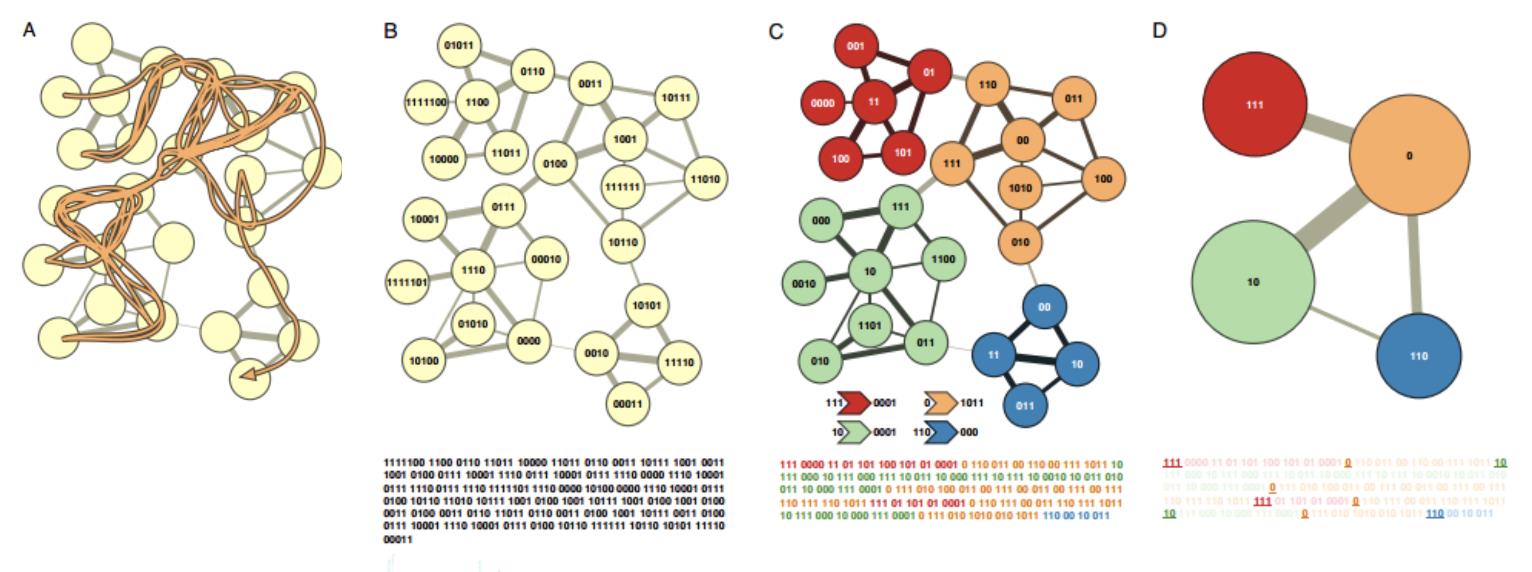
一个简单的例子
在讲完枯燥的基本概念和算法后,我们来看一个简单的例子。本例子取自《Graph Algorithms: Practical Examples in Apache Spark and Neo4j》一书中的示例的一部分。
背景是这样的:YELP,是国外类似大众点评这样的互联网应用,用户可以在上面对商家进行打分点评,也可以相互关注。下图是其内部数据的一部分,里面有四种节点:粉色为用户,蓝色为商家,红色为用户对商家点评,黄色为商家的所属分类。现在有一个需求:当某个有影响力的用户对某个商家给出差评时,要及时提醒商家采取相关措施(道歉、调整服务等等)。
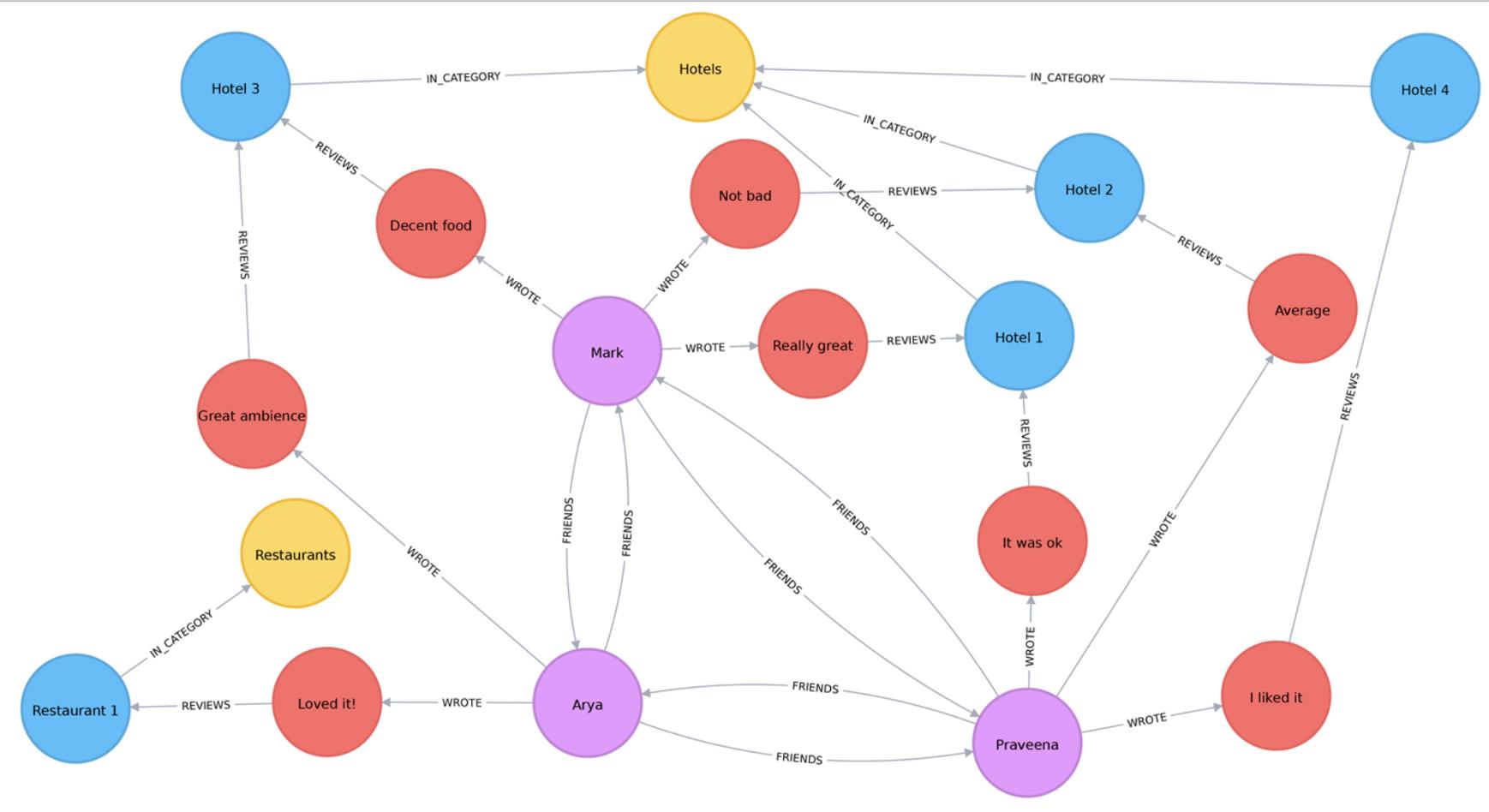
针对这样的需求,首先需要找出哪些用户是有影响力的。这里采用上文所述的PageRank算法,对每个用户计算其PageRank分值。通过对计算出来的分值进行统计分析发现,99%的用户的分值低于7.71。假设这里有10万用户,那么如果我们关注TOP1000的用户的话,只需要看用户的分值是否高于7.71即可。
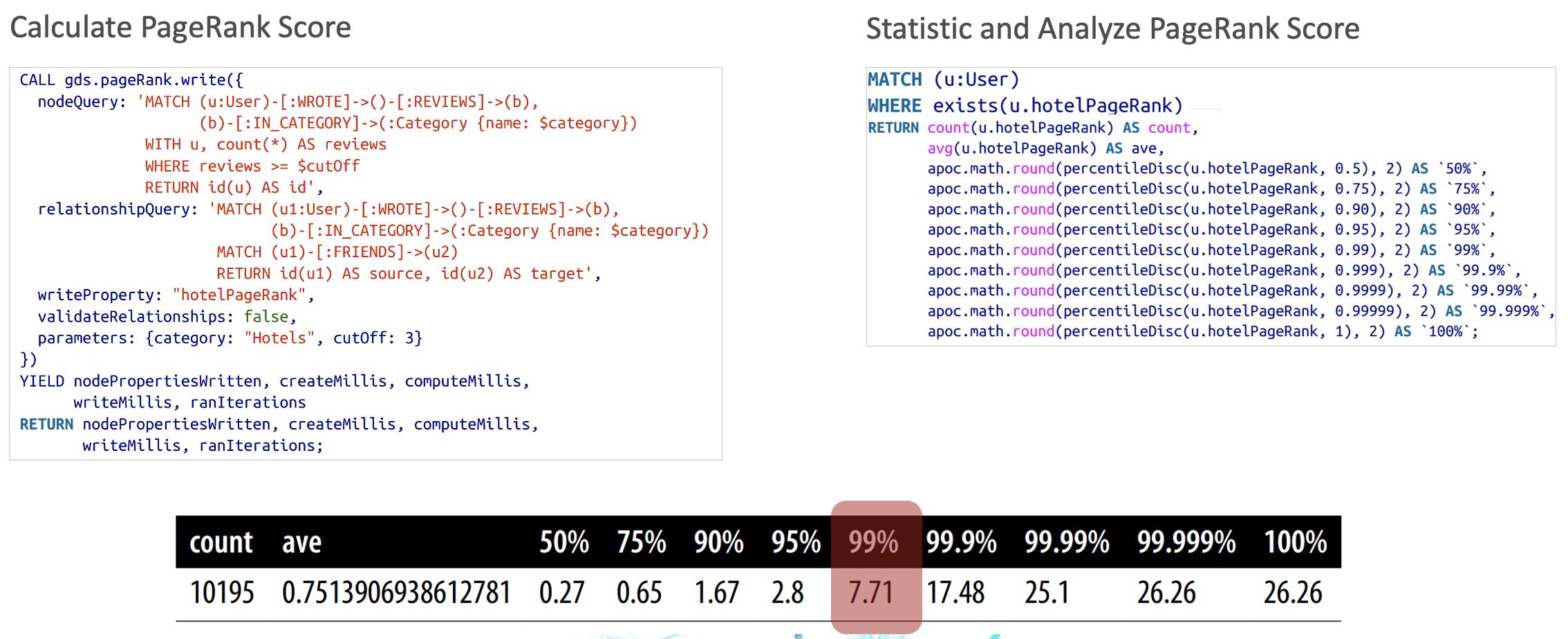
有了上述的计算与分析后,我们可以实时或者定期进行计算,找出PageRank分值高于7.71,并且给出了差评(比如打分为3分以下)的用户与商家,然后发送相关通知。

小结
本文介绍了图计算中的核心概念与算法,了解这些基本知识可以帮助我们更好更快的探索一个图,找到相应的解决方案,同时也是更深层次研究的基础。
(未完待续,本文地址:https://bruce.blog.csdn.net/article/details/112431216 )
版权声明:本人拒绝不规范转载,所有转载需征得本人同意,并且不得更改文字与图片内容。大家相互尊重,谢谢!
Bruce
2021/01/10 晚
以上是关于图计算思维与实践 核心概念与算法的主要内容,如果未能解决你的问题,请参考以下文章