裂缝识别基于matlab计算机视觉断裂裂缝识别含Matlab源码 2049期

Posted 2022-08-26 海神之光

一、简介

1 案例背景
随着国家对公路建设的大力投入，我国的公路通车总里程己经位居世界前列，这样进一步促进了我国经济建设的发展。随着公路的大量投运，公路日常养护和管理已经成为制约公路运营水平提高的瓶颈，特别是路面状态采集、检测维护等工作更是对传统的公路运维模式提出了挑战。路面裂缝是公路日常养护管理中最常见的路面损坏，也是影响公路状态评估和进行必要的公路维修的重要因素!。一般而言，如果路面裂缝能够在被恶化成坑槽之前得到及时修补，则可以大大节约公路的养护成本。传统的公路裂缝检测主要是人工检测，需要配置一定规模的人力、设备等资源来进行定期巡检。但是，面对日益增长的公路建设需求，人工检测具有运营效率低、主观性影响大、危险性较高等不足，已无法满足公路破损快速检测的要求。
随着计算机硬件设备和数字图像处理技术的发展，基于视觉的目标定位及检测技术也取得了不断的进步，由于其具有定位准确、检测快速、自动化操作、易于安装部署等特点，已经广泛应用于工业自动化检测过程，特别是在目标表面质量检测、目标物测量等领域的应用。因此，基于数字图像的路面裂缝检测技术可以提供一个安全、高效、成本低廉的道路状态监控服务，已有多种图像处理方法应用于路面裂缝检测并在一定程度上取得了实际应用。

2 理论基础
路面裂缝检测从视觉上来看是典型的线状目标检测，因此路面裂缝图像的增强与定位属于线状目标检测的研究领域，路面裂缝与一般线状目标相比，具有其自身的特点：目标宽度相对较小、图像对比度较低、具有自然间断、具有分叉和杂点等，并且路面裂缝只是在视觉总体上呈现出线状特征.传统的裂缝自动检测算法，如基于阈值分割、边缘检测、小波变换等算法，往往都假设路面裂缝在整幅图像中具有较高的对比度和较好的连续性，但这种假设在实际的工程项目中往往不成立。由于受拍摄天气、路面损耗、裂缝退化等因素的影响，有一定比例的裂缝相对于路面背景具有极低的对比度，这也会引起传统裂缝检测算法的失效，因此需要在裂缝图像处理前加入一定的预处理步骤。图像预处理一般是应用于图像识别、图像表示等领域的一种前期处理。在图像的采集和传输过程中，往往会因为某些原因导致图像质量降低。例如，从视觉主观上观察图像中
的物体，可能会发觉其轮廓位置过于鲜艳而显得突兀：从被检测目标物的大小和形状来看，图像特征比较模糊、难以定位；从图像对比度的角度来看，可能会受到某些噪声的影响；从图像整体来看，可能会发生某种失真、变形等，因此，待处理图像在视觉直观性和处理可行性等方面可能存在诸多干扰，我们不妨将其统称为图像质量问题。图像预处理正是用于图像质量的改善处理，通过一定的计算步骤进行适当的变换进面突出图像中某些感兴趣的信息，消除或降低干扰信息，如图像对比度增强、图像去噪或边缘提取等处理印，一般情况下，由于裂缝图像的采集需要涉及室外作业，所得图片难免会存在一定的噪声干扰、畸变等各种问题，直接进行裂缝目标的检测和提取往往会遇到困难。因此，本案例首先将裂缝图像进行预处理，改善图像质量，进而提高实验的优化效果。图像预处理的基本方法有图像灰度变换、频域变换、直方图变换、图像去噪、图像锐化、图像色彩变换等。本案例将选择其中的部分方法来进行裂缝图像的预处理操作。
2.1 图像灰度化
自然界中绝大部分的可见光谱均能通过红®、绿(G)、蓝(B)三色光按不同比例和强度进行混合而得到， 我们将其称为RGB色彩模式。该模式以RGB模型为基础， 对图像的每个像素值的RGB分量均分配一个Uint 8类型(0~255) 的强度值。例如， 纯红色的R值为255， G值为0， B值为0； 品红色的R值为255， G值为0， B值为255。RGB图像的红、绿、蓝分量各占8位，因此是24位图像，并且不同亮度的基色混合后，会产生出256x256x 256-16777216种颜色。RGB模型图形化表示如图所示。

假设F(i， j) 为RGB模型中的某像素， 若其3种基色的亮度值相等， 则会产生灰度颜色，将该R=G=B的值称为灰度值(或者称为强度值、亮度值)。因此，灰度图像就是包含多个量化灰度级的图像。假设该灰度级用Uint 8类型数值表示， 则图像的灰度级就是256(即2°=256)。本案例所选择的灰度图像灰度级均为256，其像素灰度值为0~255的某个值，当亮度值都是255时产生纯白色，当亮度值都是0时产生纯黑色，并且亮度从0到255呈现逐渐增加的趋势。RGB图像包含了由红、绿、蓝三种分量组成的大量的色彩信息， 灰度图像只有亮度信息而没有色彩信息。针对路面裂缝图像的检测要求，一般需要去除不必要的色彩信息， 将所采集到的RGB图像转换为灰度图像。RGB图像的灰度化方法有以下几种。
（1）分量值
选取像素F(i.j)的R、G、B分量中的某个值作为该像素的灰度值，即

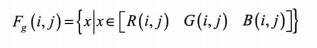
式中，Fg(i，j)为转换后的灰度图像在(i.j)处的灰度值。
（2）最大值
选取像素F(i，j)的R、G、B分量中的最大值作为该像素的灰度值，即

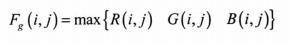
（3）平均值
选取像素F(i，j)的R、G、B分量的亮度均值作为该像素的灰度值，即

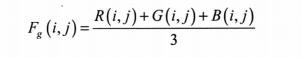
（4）加权平均值
选取像素F(i，j)的R、G、B分量的亮度加权均值作为该像素的灰度值，权值的选取一般是根据分量的重要性等指标，将3个分量以加权平均的方式进行计算得到灰度值。人眼在视觉主观上一般对绿色分量敏感度较高， 对蓝色分量敏感度较低， 因此对RGB三分量进行加权平均能得到较合理的灰度图像，常用的计算公式如下：
F.(i.j)=0.299R(i，j)+0.587G(i，j)+0.114*B(i，j)
采用加权平均计算灰度图像的方式对裂缝图像进行灰度化，所得结果如图所示。

2.2 图像滤波
裂缝图像在采集或传输的过程中往往会受到成像设备与传输介质等因素的干扰而产生噪声，因此待处理的裂缝图像可能会存在边缘模糊、黑白杂点等问题，这在一定程度上会对裂缝目标的检测和识别产生影响，干扰实验结果的判断，因此需要对裂缝图像进行滤波去噪。本节将从均值滤波和中值滤波两方面来进行图像去噪的处理。均值滤波也称为邻域平均滤波，该方法假设待处理图像是由许多灰度值为常量的小区域组成的，并且相邻区域间存在较高的空间相关性，而噪声则显得相对独立。因此，通过将单个像素及其指定邻域内的所有像素按某种规则计算平均灰度值，再作为新图像中的对应像素值，可达到滤波去噪的目的，这一过程被称为均值滤波。邻域平均法属于非加权邻域平均范畴，是最常用的均值滤波操作。
图像边缘一般集中了图像的细节和高频信息，如果通过邻域平均法进行去噪，则往往会引起图像边缘的模糊，这也会对裂缝目标的检测带来不利影响。中值滤波是常用的非线性滤波方法，其主要思想是对像素邻域向量化取中值来进行滤波，具有运算简单、高效，能有效去除脉冲噪声的特点，在去噪的同时它也可以有效地保护图像的边缘细节信息。因此，本案例将采用中值滤波的方法来对裂缝图像进行去噪处理，其处理步骤如下。
(1)定位
在图像中移动模板，将模板中心与图像中的某个像素重合。
(2)计算
选择模板对应于图像的各像素灰度值，进行向量化，并将其进行排序。
(3)赋值
选择序列的中间值，作为输出赋予模板中心对应的像素。
如图2所示，根据中值滤波器形状和维数的不同，其模板有线形、十字形、方形、菱形等，不同形状的窗口也会产生不同的滤波效果。在对裂缝图像进行中值滤波处理时，其关键在于选择合适的模板形状和模板大小。

2.3 图像增强
路面裂缝图像的采集一般在室外进行，容易受到大气、光照、机械振动等因素的影响，采集到的裂缝图像可能存在整体偏暗或偏亮等问题，进而产生对比度较低的图像。此类图像的特点是灰度分布范围较小，集中在少量的灰度区间内，这也给后续的裂缝检测和识别带来了不利影响，因此需要对此类图像进行增强处理来提高对比度。直方图作为图像灰度级分布的统计表，能在一定程度上反映图像的对比度详情。图像的灰度直方图表示该图像所属灰度类型中不同灰度级像素出现的相对频率，并且直方图的横坐标表示灰度，纵坐标表示灰度出现的次数或概率。直方图均衡化利用灰度直方图进行图像对比度的调整，以达到增强图像视觉效果的目标。直方图均衡化的基本思想是通过某种变换，将原始图像的灰度直方图从集中于某个较小的灰度区间变成在更大灰度区间内均匀分布的形式，得到灰度级差式分布，从而达到增强图像整体对比度的目标。裂缝图像区域通常属于颜色较暗的灰度区间，背景区域则属于相对较亮的灰度区间。但在采集裂缝图像的过程中，往往会由于天气干扰、曝光不足等原因而造成图像整体偏暗，使裂缝区域与背景区域亮度特征相近而不易辨别，如图所示。从原始裂缝图像的灰度直方图可以看出，其灰度值分布主要集中在0_{100的低层次灰度区间。因此，为了提高裂缝与背景的对比度，需要将原图像的灰度值范围进行扩大，形成较为明显的灰度级差，进而增加裂缝图像的对比度。经过灰度直方图均衡化处理，裂缝图像的灰度范围扩到了0}255，得到对比度增强后的裂缝图像，更加突出了裂缝与背景的差异程度。
2.4 图像二值化
灰度图像二值化是指通过约定一个灰度阈值来分割目标与背景，在阀值之内的像素于目标即记为1，其他则属于背景即记为0。在裂缝目标检测与识别的过程中，可以采用裂缝边缘、面积等特征来进行判别，也可以采用裂缝目标与周围背景的灰度差异值作为个判别依据，这就要求引入阈值来进行图像二值化处理。假设一幅灰度裂缝图像用f(x，y)表示，其中，(x，y)表示图像中像素的位置坐标，T为阈值，则阈值分割后的二值图像b(x，y)满足：

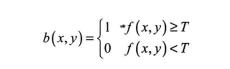
裂缝目标或背景区域的像素灰度通常是高度相关的，但裂缝目标与背景区域之间的灰度值则通常存在较大差异，一般包含明显的边缘等特征。因此，为了从更大程度上分割裂缝目标与背景，则需要对其进行灰度阈值分割选取合适的阈值。阈值计算方法根据其计算过程可以分为两种：全局阈值和基本自适应阈值，如下所述。
(1)全局阈值是最常见的阈值计算方法，它一般以图像的直方图或灰度空间分布为基础来确定一个阈值，进而实现灰度图像的二值化。特别是当图像的灰度直方图分布呈双峰时，全局阈值法可以明显地将目标和背景分量，得到较为理想的图像分割效果。但裂缝图像一般具有光照不均匀、噪声干扰等特点，其灰度直方图往往不会呈双峰分布，因此全局阈值分割方法效果较差。
(2)基本自适应阀值是一种比较基础的图像自适应分割方法，它一般以图像像素自身及其邻域灰度变化的特征为基础进行阈值分割，进而实现灰度图像的二值化。该方法充分考虑了每个像素邻域的特征，所以一般能更好地突出目标和背景的边界。
裂缝图像的背景在多数情况下比较固定，如路面、桥面、墙体等。但由于图像采集一般在室外进行，会受到拍摄条件、路面杂物等因素的影响，所以图像容易出现退化或噪声干扰。本案例通过分析裂缝图像目标和背景的特点，采用自定义和迭代法优化相结合的方法。

3 程序实现
根据裂缝图像的特点，在对其进行目标检测和识别之前，需要进行图像预处理，主要包括：直方图均衡化增强、中值滤波去噪、对比度增强、二值化处理、二值图像滤波等步骤。其中，在二值化过程中对阈值的确定选择自定义阈值法与迭代自适应法相结合的方式来计算；二值图像滤波主要是连通区域的面积滤波，通过去除小面积的杂点噪声来进行滤波去噪。裂缝图像经过预处理可以得到突出裂缝目标的二值图像，然后可以根据形态学区域特征来获取裂缝目标并进行检测识别。对于裂缝的形状识别可以通过计算图像中裂缝目标的外接矩形的长宽比来确定。

二、部分源代码

function [PC, or, ft, T] = phasecongmono(varargin)

% Get arguments and/or default values    获取参数和/或默认值
[im, nscale, minWaveLength, mult, sigmaOnf, k, ...
 noiseMethod, cutOff, g, deviationGain] = checkargs(varargin(:));  

epsilon         = .0001;            % Used to prevent division by zero.用于防止除零。

[rows,cols] = size(im);
IM = perfft2(im);                   % Periodic Fourier transform of image图像的周期性傅里叶变换

sumAn  = zeros(rows,cols);          % Matrix for accumulating filter response
                                    % amplitude values.用于累积滤波器响应振幅值的矩阵。
sumf   = zeros(rows,cols);                                  
sumh1  = zeros(rows,cols);                                      
sumh2  = zeros(rows,cols);                                          

% Generate grid data for constructing filters in the frequency domain 
%生成用于构建频域滤波器的网格数据
[radius, u1, u2] = filtergrid(rows, cols);    

% Get rid of the 0 radius value in the middle (at top left corner after
% fftshifting) so that taking the log of the radius, or dividing by the
% radius, will not cause trouble.摆脱中间的0半径值（在fftshifting之后的左上角），
%以便取半径的对数或除以半径不会造成麻烦。
radius(1,1) = 1;

% Construct the monogenic filters in the frequency domain.  The two
% filters would normally be constructed as follows在频域构建单基因滤波器。 两个滤波器通常如下构造
%    H1 = i*u1./radius; 
%    H2 = i*u2./radius;
% However the two filters can be packed together as a complex valued
% matrix, one in the real part and one in the imaginary part.  Do this by
% multiplying H2 by i and then adding it to H1 (note the subtraction
% because i*i = -1).  When the convolution is performed via the fft the
% real part of the result will correspond to the convolution with H1 and
% the imaginary part with H2.  This allows the two convolutions to be
% done as one in the frequency domain, saving time and memory.
%然而，两个滤波器可以作为复值矩阵打包在一起，一个在实部，一个在虚部。
%通过将H2乘以i然后将其添加到H1（注意因为i * i = -1）的减法）来执行此操作。
%当通过fft执行卷积时，结果的实部将对应于具有H1和具有H2的虚部的卷积。 这允许两个卷积在频域中完成，从而节省时间和记忆。
H = (1i*u1 - u2)./radius;

% The two monogenic filters H1 and H2 are not selective in terms of the
% magnitudes of the frequencies.  The code below generates bandpass
% log-Gabor filters which are point-wise multiplied by IM to produce
% different bandpass versions of the image before being convolved with H1
% and H2两个单基因滤波器H1和H2在频率的幅度方面不是选择性的。
%下面的代码生成带通对数Gabor滤波器，它们在与H1和H2进行卷积之前，以点向乘以IM产生不同的带通版本的图像

% First construct a low-pass filter that is as large as possible, yet falls
% away to zero at the boundaries.  All filters are multiplied by
% this to ensure no extra frequencies at the 'corners' of the FFT are
% incorporated as this can upset the normalisation process when
% calculating phase congruency
%首先构造尽可能大的低通滤波器，然后在边界处降到零。
%所有滤波器都乘以这一点，以确保在FFT的“拐角处”没有额外的频率被并入，因为这会在计算相位一致性时扰乱归一化过程
lp = lowpassfilter([rows,cols],.45,15);    % Radius .4, 'sharpness' 15锐度

for s = 1:nscale
    wavelength = minWaveLength*mult^(s-1);
    fo = 1.0/wavelength;                  % Centre frequency of filter.过滤器的中心频率。
    logGabor = exp((-(log(radius/fo)).^2) / (2 * log(sigmaOnf)^2));  
    logGabor = logGabor.*lp;              % Apply low-pass filter通过低通滤波器
    logGabor(1,1) = 0;                    % Set the value at the 0 frequency point of the 
                                          % filter back to zero (undo the radius fudge).

%将滤波器的0频点处的值设置为零（撤消半径软键）。
IMF = IM.*logGabor; % Bandpassed image in the frequency domain.频域中的带通图像。
f = real(ifft2(IMF)); % Bandpassed image in spatial domain.空间域中的带通图像。

    h = ifft2(IMF.*H);        % Bandpassed monogenic filtering, real part of h contains
                              % convolution result with h1, imaginary part
                              % contains convolution result with h2.带通式单基因过滤， h的实部包含h1的旋转结果，
                              %虚部包含h2的卷积结果。
    h1 = real(h); 
    h2 = imag(h);                                  
    An = sqrt(f.^2 + h1.^2 + h2.^2); % Amplitude of this scale component.该尺度下的振幅
    sumAn = sumAn + An;              % Sum of component amplitudes over scale.分量幅度的总和超过规模。
    sumf  = sumf  + f;
    sumh1 = sumh1 + h1;
    sumh2 = sumh2 + h2;  
    
    % At the smallest scale estimate noise characteristics from the
    % distribution of the filter amplitude responses stored in sumAn. 
    % tau is the Rayleigh parameter that is used to describe the
    % distribution.在最小尺度上估计来自存储在sumA中的滤波器幅度响应的分布的噪声特性。
    %tau是用于描述分布的瑞利参数。
    if s == 1 
        if noiseMethod == -1     % Use median to estimate noise statistics使用中位数估计噪声统计
            tau = median(sumAn(:))/sqrt(log(4));
        elseif noiseMethod == -2 % Use mode to estimate noise statistics使用模式估计噪声统计
            tau = rayleighmode(sumAn(:));
        end
        maxAn = An;
    else
        % Record maximum amplitude of components across scales.  This is needed
        % to determine the frequency spread weighting.记录尺度上组件的最大振幅。
        %这需要确定频率扩展权重。
        maxAn = max(maxAn,An);   
    end
                                
end   % For each scale

% Form weighting that penalizes frequency distributions that are
% particularly narrow.  Calculate fractional 'width' of the frequencies
% present by taking the sum of the filter response amplitudes and dividing
% by the maximum component amplitude at each point on the image.  If
% there is only one non-zero component width takes on a value of 0, if
% all components are equal width is 1.
%形成权重，惩罚特别窄的频率分布。通过取滤波器响应幅度的和并除以图像上每个点的最大分量幅度，
%计算存在的频率的分数“宽度”。 如果只有一个非零分量宽度取值为0，如果所有分量相等，则宽度为1。
width = (sumAn./(maxAn + epsilon) - 1) / (nscale-1);    

% Now calculate the sigmoidal weighting function.现在计算sigmoidal 加权函数。
weight = 1.0 ./ (1 + exp( (cutOff - width)*g)); 

% Automatically determine noise threshold
%
% Assuming the noise is Gaussian the response of the filters to noise will
% form Rayleigh distribution.  We use the filter responses at the smallest
% scale as a guide to the underlying noise level because the smallest scale
% filters spend most of their time responding to noise, and only
% occasionally responding to features. Either the median, or the mode, of
% the distribution of filter responses can be used as a robust statistic to
% estimate the distribution mean and standard deviation as these are related
% to the median or mode by fixed constants.  The response of the larger
% scale filters to noise can then be estimated from the smallest scale
% filter response according to their relative bandwidths.
%自动确定噪声阈值假设噪声为高斯，滤波器对噪声的响应将形成瑞利分布。 
%我们使用最小规模的滤波器响应作为底层噪声电平的指南，因为最小的滤波器花费大部分时间来响应噪声，
%只有 偶尔回应功能。滤波器响应分布的中值或模式可以用作鲁棒统计量来估计分布均值和标准偏差，
%因为它们与固定常数的中值或模式相关。然后可以根据其相对带宽从最小尺度滤波器响应估计较大比例滤波器对噪声的响应。
% This code assumes that the expected reponse to noise on the phase
% congruency calculation is simply the sum of the expected noise responses
% of each of the filters.  This is a simplistic overestimate, however these
% two quantities should be related by some constant that will depend on the
% filter bank being used.  Appropriate tuning of the parameter 'k' will
% allow you to produce the desired output. (though the value of k seems to
% be not at all critical)该代码假设在相位一致性计算上对噪声的预期响应仅仅是每个滤波器的预期噪声响应的总和。
%这是一个简单的过高估计，但是这两个数量应该与一些常数相关，这将取决于所使用的滤波器组。
%参数“k”的适当调整将允许您产生所需的输出。 （尽管k的价值似乎并不重要）

if noiseMethod >= 0     % We are using a fixed noise threshold我们正在使用固定噪声阈值
    T = noiseMethod;    % use supplied noiseMethod value as the threshold使用提供的噪声方法值作为阈值
else
    % Estimate the effect of noise on the sum of the filter responses as
    % the sum of estimated individual responses (this is a simplistic
    % overestimate). As the estimated noise response at succesive scales
    % is scaled inversely proportional to bandwidth we have a simple
    % geometric sum.估计噪声对过滤器响应的总和的影响作为估计的单个响应的总和（这是一个简单的过高估计）。
    %由于随机尺度的估计噪声响应与带宽成反比，我们有一个简单的几何和。
    totalTau = tau * (1 - (1/mult)^nscale)/(1-(1/mult));
    
    % Calculate mean and std dev from tau using fixed relationship使用这些参数和tau之间的固定关系计算tau的平均值和标准差。
    % between these parameters and tau. See
    % http://mathworld.wolfram.com/RayleighDistribution.html
    EstNoiseEnergyMean = totalTau*sqrt(pi/2);        % Expected mean and std
    EstNoiseEnergySigma = totalTau*sqrt((4-pi)/2);   % values of noise energy预期噪声能量的平均值和标准值
    
    T =  EstNoiseEnergyMean + k*EstNoiseEnergySigma; % Noise threshold噪声阈值
end

%------ Final computation of key quantities -------关键数量的最终计算

or = atan(-sumh2./sumh1);   % Orientation - this varies +/- pi/2方向
or(or<0) = or(or<0)+pi;     % Add pi to -ve orientation value so that all
                            % orientation values now range 0 - pi将所有方向归入0到π中
or = fix(or/pi*180);        % Quantize to 0 - 180 degrees (for NONMAXSUP)量化到0 - 180度（对于NONMAXSUP）
                                  
ft = atan2(sumf,sqrt(sumh1.^2+sumh2.^2));  % Feature type - a phase angle特征类型 - 相位角
                                           % -pi/2 to pi/2.

energy =  sqrt(sumf.^2 + sumh1.^2 + sumh2.^2);  % Overall energy能量

% Compute phase congruency.  The original measure, 计算相位一致性
% PC = energy/sumAn 
% is proportional to the weighted cos(phasedeviation).  This is not very
% localised so this was modified to与加权cos（相位变化）成比例。 这不是很本地化，所以这被修改为
% PC = cos(phasedeviation) - |sin(phasedeviation)| 
% (Note this was actually calculated via dot and cross products.)  This measure
% approximates （注意，这实际上是通过点和交叉积来计算的。）这个度量近似
% PC = 1 - phasedeviation.  

% However, rather than use dot and cross products it is simpler and more
% efficient to simply use acos(energy/sumAn) to obtain the weighted phase
% deviation directly.  Note, in the expression below the noise threshold is
% not subtracted from energy immediately as this would interfere with the
% phase deviation computation.  Instead it is applied as a weighting as a
% fraction by which energy exceeds the noise threshold.  This weighting is
% applied in addition to the weighting for frequency spread.  Note also the
% phase deviation gain factor which acts to sharpen up the edge response. A
% value of 1.5 seems to work well.  Sensible values are from 1 to about 2.

%然而，不是使用点和交叉产品，而是更简单和更多有效地简单地使用acos（能量/ sumAn）直接获得加权相位偏差。
%注意，在下面的表达式中，不会立即从能量中减去噪声阈值，因为这将干扰相位偏差计算。
%相反，它作为加权作为能量超过噪声阈值的分数。除了频率扩展的加权之外，还应用该加权。
%还要注意用于锐化边缘响应的相位偏差增益因子。1.5似乎很好。敏感值为1到2。
PC = weight.max(1 - deviationGainacos(energy./(sumAn + epsilon)),0) …
.* max(energy-T,0)./(energy+epsilon);

%------------------------------------------------------------------
% CHECKARGS
%
% Function to process the arguments that have been supplied, assign
% default values as needed and perform basic checks.
% 处理提供的参数的功能，根据需要分配默认值并执行基本检查。
function [im, nscale, minWaveLength, mult, sigmaOnf, …
k, noiseMethod, cutOff, g, deviationGain] = checkargs(arg)

nargs = length(arg);

if nargs < 1
    error('No image supplied as an argument');
end    

% Set up default values for all arguments and then overwrite them
% with with any new values that may be supplied
%设置所有参数的默认值，然后使用可能提供的任何新值覆盖它们
im              = [];
nscale          = 4;     % Number of wavelet scales.  小波尺度  
minWaveLength   = 3;     % Wavelength of smallest scale filter. 最小尺度小波的波长   
mult            = 2.1;   % Scaling factor between successive filters. 连续滤波器之间的缩放因子。   
sigmaOnf        = 0.55;  % Ratio of the standard deviation of the
                         % Gaussian describing the log Gabor filter's
                         % transfer function in the frequency domain
                         % to the filter center frequency.    
                         %描述频域中的log Gabor滤波器传递函数的高斯标准偏差与滤波器中心频率的比率。
k               = 3.0;   % No of standard deviations of the noise
                         % energy beyond the mean at which we set the
                         % noise threshold point. 
                         %噪声能量的标准偏差不超过我们设定噪声阈值点的平均值。
                         %对于嘈杂的图像，您可能需要更改为10或20的值
noiseMethod     = -1;    % Use the median response of smallest scale
                         % filter to estimate noise statistics
                         %使用最小尺度滤波器的中值响应来估计噪声统计
cutOff          = 0.5;
g               = 10;
deviationGain   = 1.5;

% Allowed argument reading states允许参数阅读状态
allnumeric   = 1;       % Numeric argument values in predefined order
keywordvalue = 2;       % Arguments in the form of string keyword
                        % followed by numeric value
readstate = allnumeric; % Start in the allnumeric state
%数值参数值以预定义顺序以字符串关键字后跟数值的形式以allnumeric状态开始

if readstate == allnumeric
    for n = 1:nargs
        if isa(argn,'char')
            readstate = keywordvalue;
            break;
        else
            if     n == 1, im            = argn; 
            elseif n == 2, nscale        = argn;              
            elseif n == 3, minWaveLength = argn;
            elseif n == 4, mult          = argn;
            elseif n == 5, sigmaOnf      = argn;
            elseif n == 6, k             = argn;              
            elseif n == 7, cutOff        = argn;              
            elseif n == 8, g             = argn;
            elseif n == 9, deviationGain = argn;
            elseif n == 10, noiseMethod  = argn;              
            end
        end
    end
end

% Code to handle parameter name - value pairs代码来处理参数名称 - 值对
if readstate == keywordvalue
    while n < nargs
               
        if ~isa(argn,'char') || ~isa(argn+1, 'double')
            error('There should be a parameter name - value pair');
        end
        
        if     strncmpi(argn,'im'      ,2),      im =            argn+1;
        elseif strncmpi(argn,'nscale'  ,2),      nscale =        argn+1;
        elseif strncmpi(argn,'minWaveLength',2), minWaveLength = argn+1;
        elseif strncmpi(argn,'mult'    ,2),      mult =          argn+1;
        elseif strncmpi(argn,'sigmaOnf',2),      sigmaOnf =      argn+1;
        elseif strncmpi(argn,'k'       ,1),      k =             argn+1;
        elseif strncmpi(argn,'cutOff'    ,2),    cutOff =        argn+1; 
        elseif strncmpi(argn,'g'       ,1),      g =             argn+1;
        elseif strncmpi(argn,'deviation',3),     deviationGain = argn+1; 
        elseif strncmpi(argn,'noisemethod',3),   noiseMethod =   argn+1; 
        else   error('Unrecognised parameter name');
        end

        n = n+2;
        if n == nargs
            error('Unmatched parameter name - value pair');
        end
    end
end

if isempty(im)
    error('No image argument supplied');
end

if ndims(im) == 3
    warning('Colour image supplied: converting image to greyscale...')
    im = double(rgb2gray(im));
end

if ~isa(im, 'double')
    im = double(im);
end

if nscale < 1
    error('nscale must be an integer >= 1');
end

if minWaveLength < 2
    error('It makes little sense to have a wavelength < 2');
end          

三、运行结果

四、matlab版本及参考文献

1 matlab版本
2014a

2 参考文献
[1]陈健昌,张志华.融于图像多特征的路面裂缝智能化识别[J].科学技术与工程. 2021,21(24)

3 备注
简介此部分摘自互联网，仅供参考，若侵权，联系删除