神经网络回归与线性模型

Posted 2022-08-22 ViperL1

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了神经网络回归与线性模型相关的知识，希望对你有一定的参考价值。

一、线性回归

需要通过训练集 $x^{(n)}$ 和 $y^{(n)}$ 求解x,y之间的映射关系 $y=f(x,\theta )$

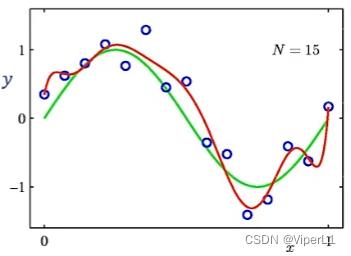
1.线性回归

①模型

$f(x;\omega ,b)=\omega^Tx+b$

增广权重向量&增广特征向量：在x和 $\omega$ 上添加一个b，可将模型中原有的b消除。

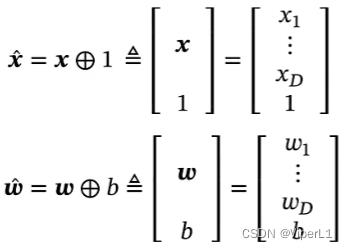
模型转换为： $f(x;\omega ,b)=\omega^Tx+b ->f(x;\omega)=\omega^Tx$

②训练集D上的经验风险

$R(\omega)=\sum_{n=1}^{N}L(y^{(n)},f(x^{(n)};\omega))=\frac{1}{2}\sum_{n=1}^{N}(y^{(n)}-\omega^Tx^{(n)})^2=\frac{1}{2}||y-X^T\omega||^2$

X矩阵：其中每行为一个样本

Y向量：列向量，每一列为一个结果

$\left| \begin{array} {ccc} x_1^{(1)},x_1^{(2)},...x_1^{(n)}\\ x_2^{(1)},x_2^{(2)},...x_2^{(n)}\\ ...\\ \end{array} \right|$ $\left| \begin{array} {ccc} y^1\\ y^2\\ ... \end{array} \right|$ $x^Tw=\left| \begin{array} {ccc} w^Tx_1^{(1)},w^Tx_1^{(2)},...w^Tx_1^{(n)}\\ w^Tx_2^{(1)},w^Tx_2^{(2)},...w^Tx_2^{(n)}\\ ...\\ \end{array} \right|$

③经验风险最小化

$\frac{\partial}{\partial w} R(w)=0$ 以此公式求解w

推导： $\frac{\partial}{\partial w} R(w)=\frac{\partial \frac{1}{2}||y-x^Tw||^2 }{\partial w}=\frac{1}{2}*-x*2(y-x^Tw)=0$

$->-xy+xx^T=0$

$->xx^Tw=xy$

$->w=(xx^T)^{-1}xy$ 条件： $(xx^T)^{(-1))}$ 必须存在

若 $(xx^T)^{(-1))}$ 不存在（特征之间存在共线性），可以采用以下两种方法求解

①SGD(随机数下降) ②降维

结构风险： $R(w)=\frac{1}{2}||y-X^Tw||^2+\frac{1}{2}\lambda ||w||^2$ ，其中 $\frac{1}{2}\lambda ||w||^2$ 被称为正则化项， $\lambda$ 为正则化参数。

使其最小化： $w^*=(XX^T+\lambda I)^{-1}Xy$

！！！Attention矩阵微积分

2.多项式回归

①模型

$f(x,w)=w_0+w_1x+w_2x^2+...+w_mx^m$ 多项式曲线拟合

②损失函数

$R(w)=\frac{1}{2}\sum_{n=1}^{N}(y^{(n)}-w^T\phi (x^{(n)}))^2$

③经验风险最小化

求解过程与线性回归类似

④选择合适的多项式次数

控制过拟合：正则化

惩罚大的系数： $R(w)=\frac{1}{2}\sum_{n=1}^N(y^{(n)}-w^T\phi (x^{(n)}))^2+\frac{\lambda}{2}w^Tw$

其中 $\frac{\lambda}{2}w^Tw$ 为正则化项， $\lambda$ 为正则化系数

控制过拟合：增加训练样本数量

3.从概率视角来看线性回归

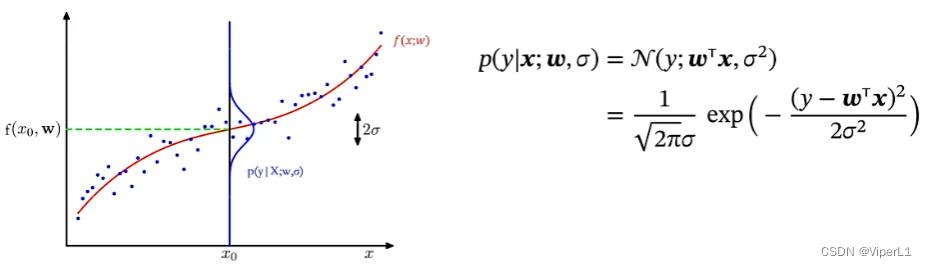
①似然函数

参数w固定时，描述随机变量x的分布情况，称p(x;w)为概率

已知随机变量x时，不同参数w对其分布的影响，称p(x;w)为似然

线性回归中的似然函数： $p(y|X;w,\sigma )=\prod_{n=1}^{N}p(y^{(n)}|x^{(n)};w,\sigma)$

$=\prod_{n=1}^{N}N(y^{(n)};w^Tx^{(n)},\sigma)$

②最大似然估计

求一组参数w，使 $p(y|X;w,\sigma )$ 取最大值（求导）

$w^{ML}=(XX^T)^{-1}Xy$

③贝叶斯学习

将参数w也视为随机变量；给定一组数据X，求参数w的分布p(w|X)，也称后验分布

贝叶斯公式： $p(y|x)=\frac{p(x|y)p(y)}{p(x)}$

先验： $p(w|x)\propto p(x|w)p(w)$ 后验正比于似然 X 先验

最大后验估计： $w^{MAP}=arg max p(y|X,w;\sigma)p(w;v)$

$=-\frac{1}{2\sigma}||y-X^T||^2-\frac{1}{2v^2}w^Tw$ 正则化系数 $\lambda=\frac{\sigma^2}{v^2}$

⑤四种准则

平方误差	经验风险最小化	$(XX^T)^{-1}Xy$
平方误差	结构风险最小化	$(XX^T+\lambda I)^{-1}Xy$
概率	最大似然估计	(XX^T)^-1Xy
概率	最大后验估计	$(XX^T+\lambda I)^{-1}Xy$