对顶堆与应用

Posted 2022-08-18 白龙码~

文章目录

• 对顶堆
• • 一、维持对顶堆的平衡
  • • 1、约定
    • 2、平衡算法
  • 二、获取中位数
  • 三、代码实现
  • 四、实战演练

对顶堆

对顶堆是一种利用一个大根堆和一个小根堆组合而成的数据结构。两个堆顶形成了一种沙漏结构，故称为对顶堆，常用于O(1)时间复杂度获取数据流的中位数。

注：不叫"沙漏堆"可能是因为不好听吧。

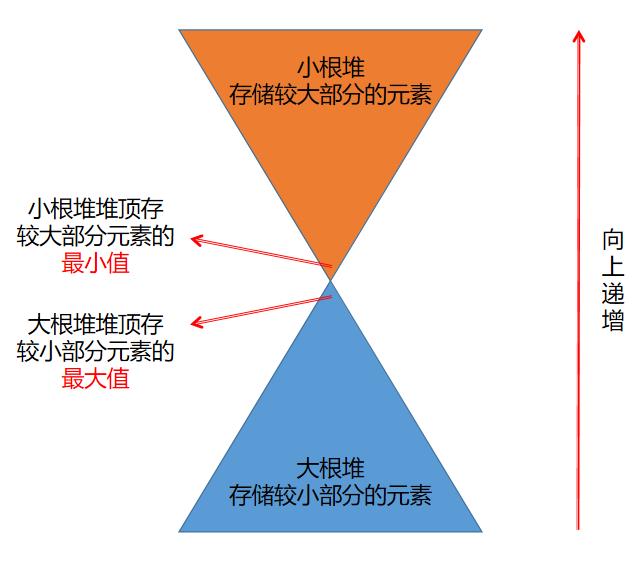
一、维持对顶堆的平衡

与AVL树和红黑树相似，对顶堆同样需要维持一种平衡，但这种平衡并不是树那样的平衡，且维护起来更为简单。

1、约定

为了维护平衡，对顶堆需要满足以下约定：

1. 较小的那一半元素使用大根堆存储，较大的那一半元素使用小根堆存储。
2. 当数据个数N为偶数时，大根堆和小根堆数据个数相同，为N/2。
3. 当数据个数N为奇数时，大根堆比小根堆多一个数据，即大根堆为N/2+1，小根堆为N/2。

综合2、3两种约定，可以总结：小根堆元素数量<=大根堆元素数量<=小根堆元素数量+1 (不能同时取等)

2、平衡算法

每个新来的数据都要插入到对应的堆中，整体分为三种情况。

情况一、大根堆为空

由于规定大根堆与小根堆数据量相同或者多一个数据，因此这种情况说明当前两个堆都为空。

此时将新数据插入到大根堆。

情况二、新元素<大根堆的堆顶元素

说明新元素属于较小的那部分元素，因此将其插入大根堆，然后分小情况判断：

1. 如果大根堆元素数量<=小根堆元素数量+1，则说明此时满足约定，无需调节。

2. 如果大根堆元素数量>小根堆元素数量+1，则说明此时不满足约定，需要调节：

   这种情况的出现只可能是大根堆元素数量=小根堆元素数量+2，因为在新元素插入之前必须满足大根堆元素数量<=小根堆元素数量+1。

   因此，只需要将大根堆的堆顶x移出，并插入到小根堆即可，这时再次满足之前的约定。

情况三、新元素>=小根堆的堆顶元素

说明新元素属于较大的那部分元素，因此将其插入小根堆，然后分小情况判断：

1. 如果小根堆元素数量<=大根堆元素数量，则说明此时满足约定，无需调节。

2. 如果小根堆元素数量>大根堆元素数量，则说明此时不满足约定，需要调节：

   这种情况的出现只可能是小根堆元素数量=大根堆元素数量+1，因为在新元素插入之前必须满足小根堆元素数量<=大根堆元素数量。

   因此，只需要将小根堆的堆顶x移出，并插入到大根堆即可，这时再次满足之前的约定。

二、获取中位数

对于满足上述约定的对顶堆，中位数的获取只需要分为两种情况：

1. 大根堆与小根堆元素数量相同，则中位数就是两个堆顶的平均值。
2. 大根堆=小根堆元素数量+1，则中位数就是大根堆的堆顶。

三、代码实现

class OppositeVertexHeap 

    // 对顶堆：
    // lpq为大根堆，存储小的那一半数据
    // gpq为小根堆，存储大的那一半数据
    // 同时约定：
    // 当数据为偶数个时，lpq与gpq的数据量相等，此时中位数就是二者堆顶元素的均值
    // 当数据为奇数个时，lqp比gpq多一个数据，此时中位数就是lpq的堆顶元素
    priority_queue<int, vector<int>, less<int>> lpq;
    priority_queue<int, vector<int>, greater<int>> gpq;
public:
    void Add(int num) 
    
        if (lpq.empty() || num < lpq.top())
        
            lpq.push(num);
            if (lpq.size() > gpq.size() + 1)
            
                // 将lpq的堆顶元素移至gpq，使满足约定
                gpq.push(lpq.top());
                lpq.pop();
            
        
        else
        
            gpq.push(num);
            if (gpq.size() > lpq.size())
            
                // 将gpq的堆顶元素移至lpq，使满足约定
                lpq.push(gpq.top());
                lpq.pop();
            
        
    
    
    double FindMedian() 
    
        if (lpq.size() == gpq.size())
        
            return (lpq.top() + gpq.top()) / 2.0;
        
        else // lpq.size() > gpq.size()
        
            // 说明中位数为lpq的堆顶
            return lpq.top();
        
    
;

四、实战演练

学会了对顶堆后，这道《剑指offer》的题就可以尝试一下了：数据流的中位数