梯度下降

Posted 2023-02-25 已删除ddd

梯度下降是机器学习中最基本的概念，分为BGD（Batch Gradient Descent）、SGD(Stochastic Gradient Descent)和MBGD（Mini-Batch Gradient Descent）三种。

线性回归函数的假设函数为

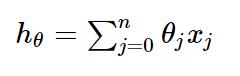
对应的损失函数为

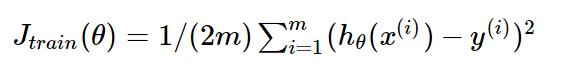
下图为一个二维参数能量函数的可视化图：

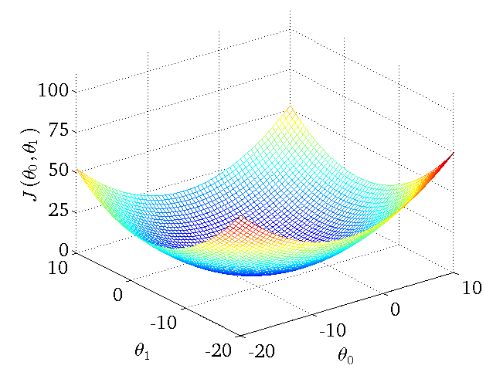
批量梯度下降BGD

• 随机初始化权重
• 通过数据不断更新权重并判断是否满足停止条件，具体做法如下

其中m代表训练数据大小，即每次梯度下降需要对全部特征用到全部训练数据，当训练集比较大的时候，批量梯度下降方法会产生严重的效率问题。

随机梯度下降SGD

由于批梯度下降每跟新一个参数的时候，要用到所有的样本数，所以训练速度会随着样本数量的增加而变得非常缓慢。随机梯度下降正是为了解决这个办法而提出的。它是利用每个样本的损失函数对θ求偏导得到对应的梯度，来更新θ：

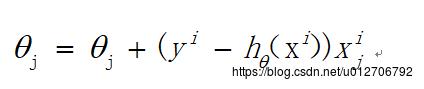
更新过程如下：

批量梯度下降同随机梯度下降比较而言， 前者用所有数据进行梯度下降，后者用一个样本进行梯度下降。各自的优缺点都非常突出。

训练速度：随机梯度下降由于每次仅仅采用一个样本来迭代，训练速度很快，而批量梯度下降法在样本量很大的时候，训练速度不能让人满意。

准确度：随机梯度下降法用于仅仅用一个样本决定梯度方向，导致解很有可能不是最优。

收敛速度：由于随机梯度下降法一次迭代一个样本，导致迭代方向变化很大，不能很快的收敛到局部最优解。

小批量梯度下降MBGD

小批量梯度下降法是批量梯度下降法和随机梯度下降法的折衷，也就是对于m个样本，我们采用x个样子来迭代，1<x<m。一般可以取x=10，当然根据样本的数据，可以调整这个x的值。对应的更新公式是：

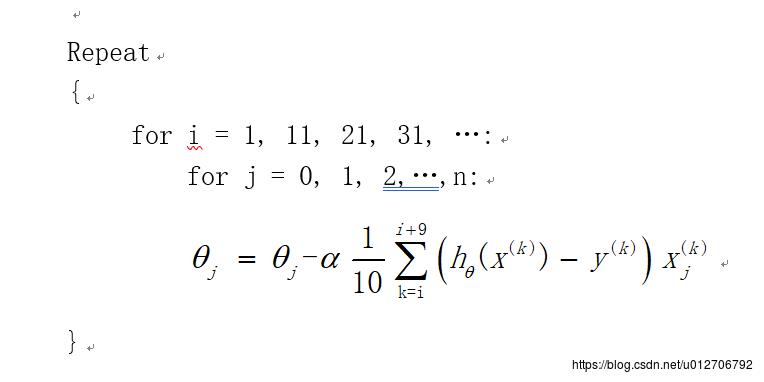
梯度下降法和其他无约束优化算法的比较

在机器学习中的无约束优化算法，除了梯度下降以外，还有前面提到的最小二乘法，此外还有牛顿法和拟牛顿法。

梯度下降法和最小二乘法相比，梯度下降法需要选择步长，而最小二乘法不需要。梯度下降法是迭代求解，最小二乘法是计算解析解。如果样本量不算很大，且存在解析解，最小二乘法比起梯度下降法要有优势，计算速度很快。但是如果样本量很大，用最小二乘法由于需要求一个超级大的逆矩阵，这时就很难或者很慢才能求解解析解了，使用迭代的梯度下降法比较有优势。

梯度下降法和牛顿法/拟牛顿法相比，两者都是迭代求解，不过梯度下降法是梯度求解，而牛顿法/拟牛顿法是用二阶的海森矩阵的逆矩阵或伪逆矩阵求解。相对而言，使用牛顿法/拟牛顿法收敛更快。但是每次迭代的时间比梯度下降法长。