LeetCode 0623.在二叉树中增加一行：DFS / BFS

Posted 2022-08-09 Tisfy

【LetMeFly】623.在二叉树中增加一行：DFS / BFS

力扣题目链接：https://leetcode.cn/problems/add-one-row-to-tree/

给定一个二叉树的根 root 和两个整数 val 和 depth ，在给定的深度 depth 处添加一个值为 val 的节点行。

注意，根节点 root 位于深度 1 。

加法规则如下:

• 给定整数 depth，对于深度为 depth - 1 的每个非空树节点 cur ，创建两个值为 val 的树节点作为 cur 的左子树根和右子树根。
• cur 原来的左子树应该是新的左子树根的左子树。
• cur 原来的右子树应该是新的右子树根的右子树。
• 如果 depth == 1 意味着 depth - 1 根本没有深度，那么创建一个树节点，值 val 作为整个原始树的新根，而原始树就是新根的左子树。

 

示例 1:

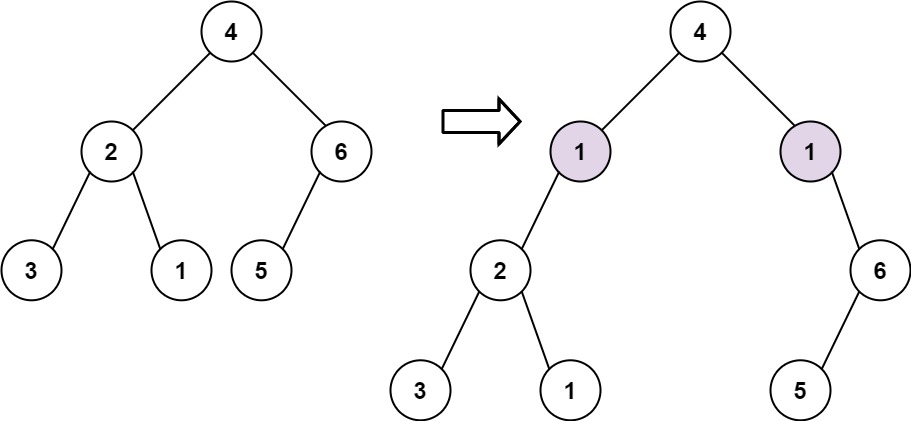
输入: root = [4,2,6,3,1,5], val = 1, depth = 2
输出: [4,1,1,2,null,null,6,3,1,5]

示例 2:

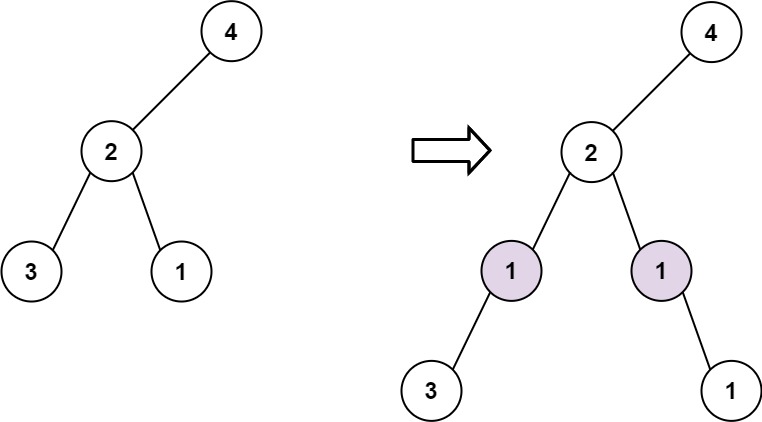
输入: root = [4,2,null,3,1], val = 1, depth = 3
输出:  [4,2,null,1,1,3,null,null,1]

 

提示:

• 节点数在 [1, 104] 范围内
• 树的深度在 [1, 104]范围内
• -100 <= Node.val <= 100
• -105 <= val <= 105
• 1 <= depth <= the depth of tree + 1

方法一.1：广度优先搜索

按照经典的 二叉树层次遍历的方法 对二叉树进行层次遍历，当遍历到对应的层的上一层时，为这一层的左右子都新建立一个值为val的新的子节点，并将新左子指向旧左子，新右子指向旧右子。

• 时间复杂度$O(n)$，其中$n$是二叉树节点的个数
• 空间复杂度$O(n)$

AC代码

C++

class Solution 
public:
    TreeNode* addOneRow(TreeNode* root, int val, int depth) 
        if (depth == 1) 
            TreeNode* newRoot = new TreeNode(val);
            newRoot->left = root;
            return newRoot;
        
        int nowLayer = 1;
        queue<TreeNode*> q;
        q.push(root);
        while (q.size()) 
            int thisLayerNodesNum = q.size();
            nowLayer++;
            for (int i = 0; i < thisLayerNodesNum; i++) 
                TreeNode* thisNode = q.front();
                q.pop();
                if (nowLayer == depth) 
                    TreeNode* leftNewNode = new TreeNode(val, thisNode->left, nullptr);
                    TreeNode* rightNewNode = new TreeNode(val, nullptr, thisNode->right);
                    thisNode->left = leftNewNode, thisNode->right = rightNewNode;
                    if (leftNewNode->left) 
                        q.push(leftNewNode->left);
                    
                    if (rightNewNode->right) 
                        q.push(rightNewNode->right);
                    
                
                else 
                    if (thisNode->left) 
                        q.push(thisNode->left);
                    
                    if (thisNode->right) 
                        q.push(thisNode->right);
                    
                
            
        
        return root;
    
;

方法一.2：广度优先搜索 + 提前退出

在方法一.1的基础上，如果我们已经新建了节点，那么就已经没有必要再遍历下去了，因为层次遍历越往下层数越深，下面的节点不需要做出任何改变。

因此，方法一.2就是在方法一.1的基础上，插入新节点后，退出遍历。

• 时间复杂度$O(n)$，其中$n$是二叉树节点的个数
• 空间复杂度$O(n)$

AC代码

C++

class Solution 
public:
    TreeNode* addOneRow(TreeNode* root, int val, int depth) 
        if (depth == 1) 
            TreeNode* newRoot = new TreeNode(val);
            newRoot->left = root;
            return newRoot;
        
        int nowLayer = 1;
        queue<TreeNode*> q;
        q.push(root);
        while (q.size()) 
            int thisLayerNodesNum = q.size();
            nowLayer++;
            for (int i = 0; i < thisLayerNodesNum; i++) 
                TreeNode* thisNode = q.front();
                q.pop();
                if (nowLayer == depth) 
                    TreeNode* leftNewNode = new TreeNode(val, thisNode->left, nullptr);
                    TreeNode* rightNewNode = new TreeNode(val, nullptr, thisNode->right);
                    thisNode->left = leftNewNode, thisNode->right = rightNewNode;

					// 相应地，这里也取消了入队操作  // -------------------
                
                else 
                    if (thisNode->left) 
                        q.push(thisNode->left);
                    
                    if (thisNode->right) 
                        q.push(thisNode->right);
                    
                
            
            
            if (nowLayer == depth)   // ------------------------
                break;  // 直接break掉即可
            
        
        return root;
    
;

方法二：深度优先搜索

为什么先讲广度优先搜索再讲深度优先搜索？

因为深搜代码比广搜要简洁许多。

深搜时，如果depth > 2，就正常地递归即可

但是当depth = 2时，就说明这一层的下一层需要插入值为val的节点。那么就对这个节点新建两个值为val的新的子节点，(类似一.1)并将新左子指向旧左子，新右子指向旧右子。

建立新节点后，就不需要再继续递归了。

特别的，如果depth = 1（除非题目原始输入就是depth为1，否则不会遇到这种情况），就按题目要求新建值为val的节点，并将原始根节点赋值为新节点的左子节点，并返回新节点。

• 时间复杂度$O(n)$，其中$n$是二叉树节点的个数
• 空间复杂度$O(n)$

AC代码

C++

class Solution   // 递归的魅力
public:
    TreeNode* addOneRow(TreeNode* root, int val, int depth) 
        if (!root) 
            return nullptr;
        
        if (depth == 1) 
            TreeNode* newRoot = new TreeNode(val, root, nullptr);
            return newRoot;
        
        if (depth == 2)   // 不必再继续递归
            root->left = new TreeNode(val, root->left, nullptr);
            root->right = new TreeNode(val, nullptr, root->right);
        
        else 
            addOneRow(root->left, val, depth - 1);
            addOneRow(root->right, val, depth - 1);
        
        return root;
    
;

同步发文于CSDN，原创不易，转载请附上原文链接哦~
Tisfy：https://letmefly.blog.csdn.net/article/details/126179967