Polygon zkEVM 基本概念

Posted mutourend

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了Polygon zkEVM 基本概念相关的知识，希望对你有一定的参考价值。

1. 引言

前序博客有：

Polygon zkEVM为zk-rollup layer 2扩容方案，其：

  • execute smart contracts transparently
  • publish zero-knowledge validity proof
  • 与以太坊虚拟机opcode完全兼容——为此需重建所有EVM opcodes，从而支持transparent deployment of any existing Ethereum smart contract。

开源代码见：

各代码库有：

Core ReposSpecific Tools & LibrariesGeneric Tools & Libraries
zkevm-proverjszkevm-commonjspilcom
zkevm-romzkasmcompil-stark
zkevm-proverzkevm-testvectors
zkevm-nodezkevm-storagerom
zkevm-contracts
zkevm-bridge-service
zkevm-bridge-ui
zkevm-doc

2. EVM Arithmetization

证明某EVM交易执行正确的第一步是：

  • 构建一个合适的execution trace。

所谓execution trace，是指满足EVM processing约束的一组值。将execution trace以矩阵表示，每列具有一个name。将每列插值为一个多项式，将execution的正确性 最终reduce为 验证多项式之间（列之间） 的一组identities。设计合适的列和identities的过程 称为 arithmetization。

Polygon zkEVM提供了an efficient arithmetization of the EVM。

3. Executor, zkASM 和 zkProver

由Executor负责创建execution trace。
Executor的输入有：

  • 1）a batch of 交易
  • 2）a chain ID
  • 3）代表该链zkEVM previous state的Merkle tree root
  • 4）代表这些交易执行之后的该链zkEVM new state的Merkle tree root
  • 5）values of the current state of the zkEVM，以构建proof

Executor本质上是一种名为zkASM的汇编语言解释器。
使用zkASM语言来构建名为zkROM的程序，Executor运行zkROM程序来提供合适的execution trace。

在zkROM程序中，每个EVM opcode都以一组zkASM指令集来实现。
每个zkASM指令利用了execution trace矩阵中的一行，又名zkEVM的一个“step”。

Executor为zkProver的一部分，zkProver为Polygon zkEVM的核心部件。

zkProver与节点和Database（DB）之间的交互流程为：

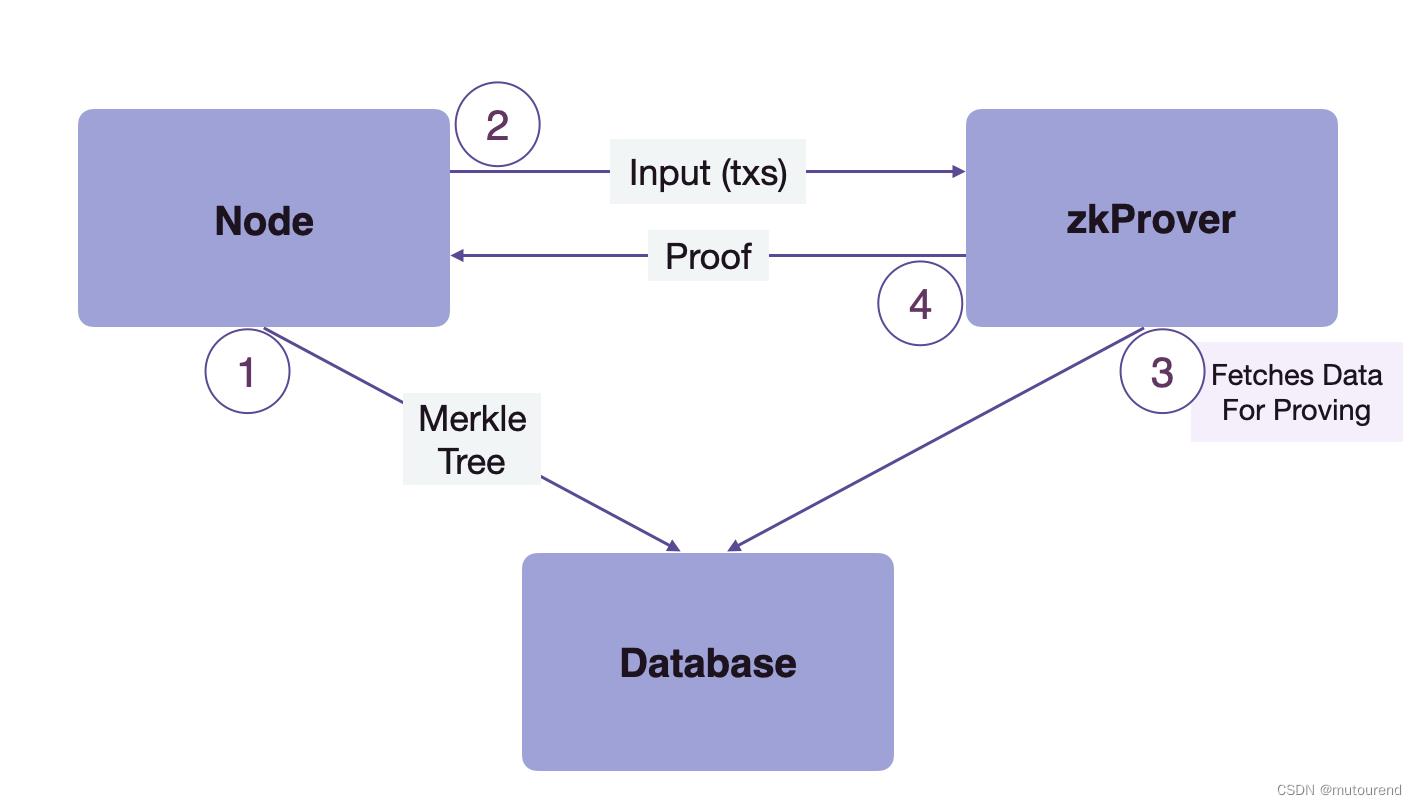
  • 1）节点将Ethereum state content和EVM Merkle trees发送到DB并存储。
  • 2）节点将input batch of transactions发送到zkProver。
  • 3）zkProver访问DB，获取 为节点发送的transaction batch 生成verifiable proof 所需的信息。
  • 4）zkProver为交易生成证明，将proof发回给节点。

3.1 zkProver中的状态机

zkProver采用模块化设计，主要由14种state machines组成：

  • 1）1个Main State Machine
  • 2）6个Secondary State Machine：Binary SM、Storage SM、Memory SM、Arithmetic SM、Keccak Function SM、Poseidon SM。
  • 3）7个Auxiliary State Machine：Padding-PG SM、Padding-KK SM、Nine2One SM、Memory Align SM、Norm Gate SM、Byte4 SM、ROM SM。

zkProver这种模块化的设计，使得Main SM可将其职责委托给尽可能专业的state machine，通过委托实现效率的提升。

3.1.1 Secondary State Machine

Main SM Executor直接向secondary state machine发送名为Actions的合适指令 来传达命令。

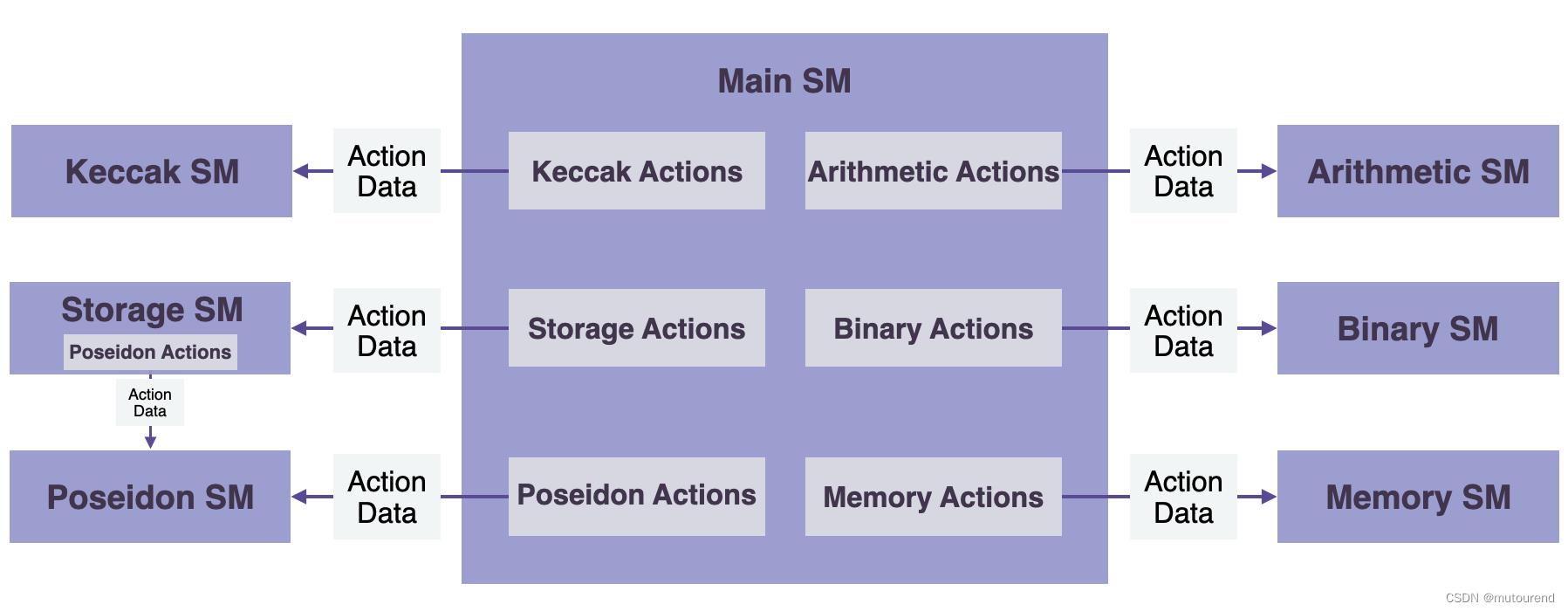
上图灰色方框即表示的是Actions。这些指令会命令 某state machine内的state如何transition。无论是来自Main SM还是来着特定SM的“Action”，每个Action都必须附加一个proof以证明其执行的正确性。
SM之间有一些相互依赖：

  • 1）Storage SM会使用Merkle Trees和Poseidon SM，因其需要计算Storage Merkle Tree中所有节点的哈希值。
  • 2）Keccak SM和Poseidon SM均为哈希转太极，对应的辅助状态机有Padding-KK SM和Padding-PG SM。

3.1.2 zkProver的2种编程语言

Polygon Hermez团队为zkProver创建了2种编程语言：

  • 1）zkASM：Zero-Knowledge Assembly language。zkASM负责将zkProver Main SM的指令映射到其它SM。若SM有firmware，则zkASM为该firmware的解析器。
    zkASM代码的输入为 来自Main SM的指令，输出为 生成特定SM Executor如何运行计算的特定assembly codes。该Executor会严格遵循zkASM代码的规则和逻辑，从而可很容易地验证计算。

  • 2）PIL：Polynomial Identity Language。因为几乎所有的状态机都将计算表示为多项式。状态机内状态变化必须满足特定计算相关的polynomial identities。
    Polygon zkEVM项目的主要目的是解决区块链不可能三角问题：隐私性、安全性、可扩展性，其本质是一种高效零知识承诺机制。而当前最安全和高效的承诺机制为多项式承诺机制，将计算转换成某种多项式语言是有利的，在这种语言中，验证归结为测试执行是否满足某些多项式恒等式（identities）。
    zkProver状态机内的所有PIL代码，构成了verifier code的DNA。
    Polynomial Identity Language（PIL）为定义state machine execution trace约束的领域特定语言。
    PIL用于：

    • 定义execution trace多项式name
    • 描述多项式identities
    • 描述多项式之间关系

    以满足execution是正确的。

3.1.3 Micro-Processor Context——Main SM和Storage SM

zkProver中有2种微处理器类型的状态机：

  • Main SM
  • Storage SM

这2种微处理器类型的状态机有：

  • 1）firmware 固件部分：运行zkASM语言，以设置逻辑和规则，以JSON格式表示并存储在ROM中。特定的SM Executor将解析该JSON文件，然后根据JSON文件中的规则和逻辑执行Storage Actions。
  • 2）hardware 硬件部分：运行PIL语言，以定义约束（或polynomial identities），以JSON格式表达并存储在相应的JSON文件内。与firmware类型，特定的SM Executor会解析这些约束，因为所有的计算都必须与polynomial identities一致。


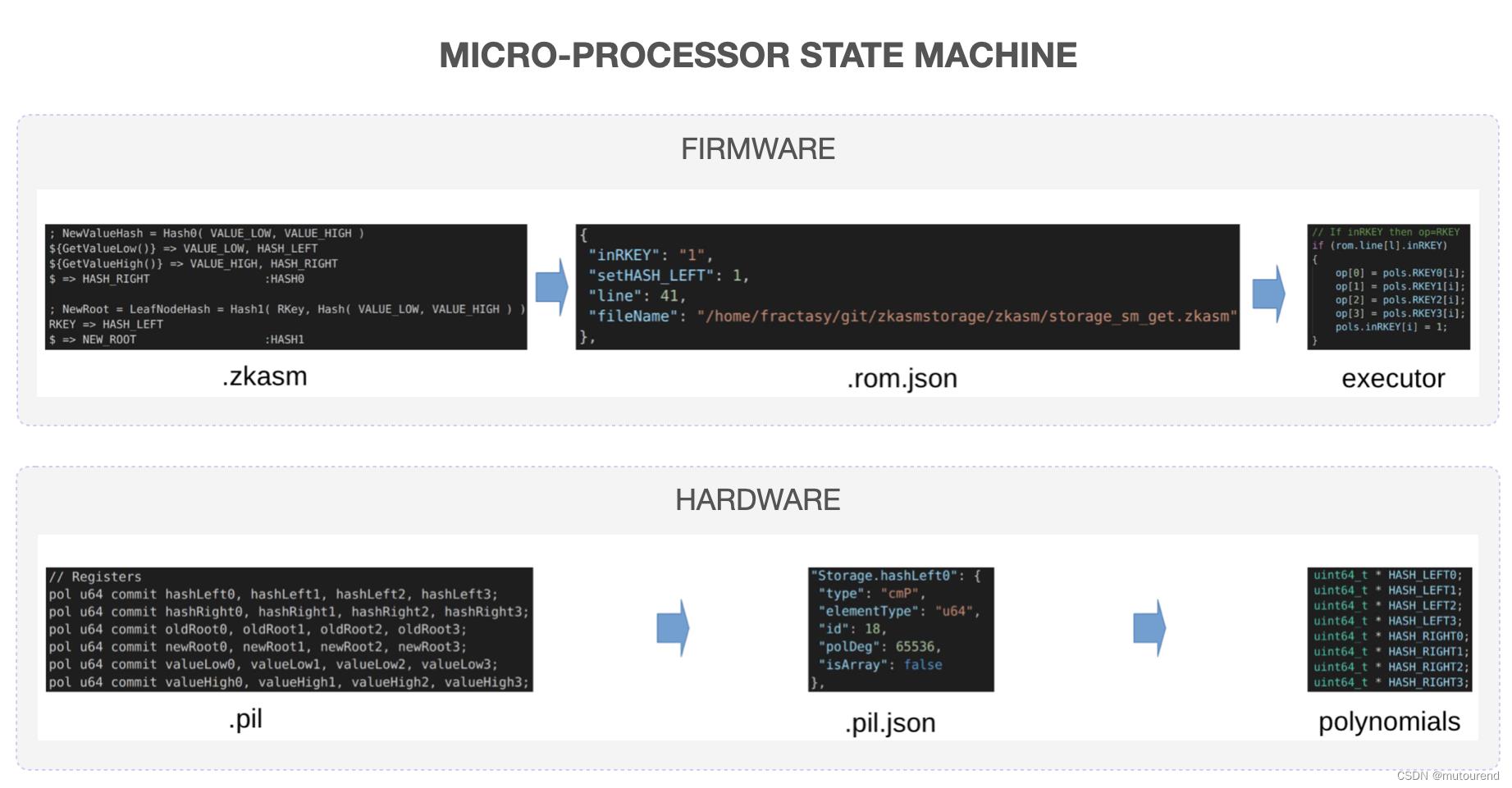
尽管Main SM和Storage SM看起来跟上图一样，但是二者区别很大：

  • Storage SM擅长执行Storage Actions（又名SMT Actions），而Main SM负责更广范围的Actions。
  • Main SM将大多数的Actions委托给专门的状态机，Storage SM是Secondary状态机——因其也从Main SM接收指令，但Storage SM无法给Main SM发送指令。

值得注意的是，每个微处理SM有各自的ROM。

3.1.4 zkProver中的哈希

有2个二级状态机负责哈希运算，二者均为标准密码学哈希函数的“automised”版本：

  • 1）Keccak SM：为gates state machine，有一系列逻辑门（硬件）和一系列门（逻辑）之间的connections。由Keccak SM Hash Generator和Keccak PIL code组成，其中Keccak PIL code用于validation。
  • 2）Poseidon SM：Poseidon哈希要比Keccak哈希算法更新，当前仍处于密码分析师的scritiny中，为zk-STARK-friendly hash function，其很适合于zkProver上下文。
    若熟悉原始Poseidon哈希函数的内部机制，Poseidon SM的实现非常直观。
    哈希函数的permutation过程很容易转化为Poseidon SM的状态转换。哈希函数的12个输入元素、非线性替换层（S-boxes）和线性扩散层（MDS矩阵）直接在状态机中实现。
    尽管Poseidon SM是二级状态机，它同时会从Main SM和Storage SM中接收指令。
    Poseidon SM有：
    • 2.1）executor部分
    • 2.2）internal PIL code：为验证规则集，以PIL语言编写。

3.2 证明每个状态机内计算正确执行的基本方法

zkProver的状态机设计为：

  • 运行程序
  • 并证明“程序执行正确”

每个二级状态机内包含了：

  • 1）其自身的executor
  • 2）一个PIL程序：用于检查其收到的源自Main SM的指令执行正确。

系统实现交易的证明和验证的基本流程为：

  • 1）将某指定计算表示为状态机SM。
  • 2）将该状态机的状态变化表示为多项式。
  • 3）跟踪状态变化的trace，称为execution trace，作为lookup表的行。
  • 4）形成该状态变化所满足的polynomial identities/constraints。
  • 5）“Prover”采用特定的多项式承诺机制来承诺和证明其知道所commit的多项式。
  • 6）Plookup是一种检查Prover的committed polynomials 是否produce correct trace的方法。

多项式约束以PIL语言编写，而指令初始以zkASM语言编写，然后以JSON格式表达和存储。
尽管并不是所有的verification都包含了Plookup，但确实Plookup在zkProver中承担的了重要角色：

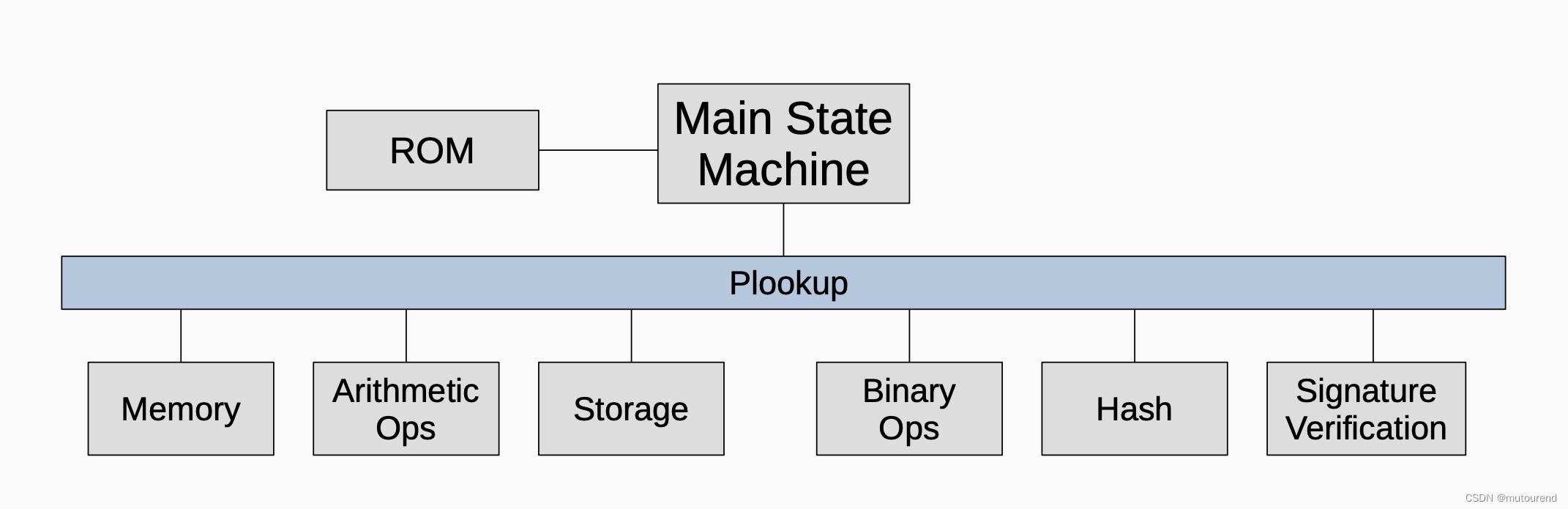
3.3 zkProver核心元素

zkProver主要有4大核心元素：

  • 1）Executor，此处是指Main SM Executor：以交易、执行交易前的old states root、执行交易后的new states root、Sequencer的ChainID等，以及 PIL（为一组多项式、寄存器）和ROM（存储了需执行的指令集）为输入，Executor在PIL hardware层执行所有指令，并生成committed多项式——为state machine cycles 或 a list of all the states，同时还会生成某些public data——作为zk-SNARK Verifier的输入。【Main SM Executor负责将交易和相关数据转换为committed多项式】
  • 2）STARK Recursion元素：输入有：committed多项式、constant多项式、scripts（指令集），输出为a zk-STARK proof。为了利用zk-STARK的快速证明，STARK Recursion中为每个zk-proof利用了FRI。之所以称为STARK Recursion，是因为：【即数百个zk-STARK proof会递归证明为一个zk-STARK proof】
    • a）其确实生成了多个zk-STARK proof
    • b）将这些zk-STARK proof整理捆绑为少量几个zk-STARK proof bundle
    • c）为每个bundle生成了zk-STARK proof
    • d）该bundle的zk-STARK proof会进一步整理并证明为一个zk-STARK proof。
  • 3）CIRCOM库：输入为：STARK Recursion元素生成的单个zk-STARK proof、Verifier Data，输出为：Witness。zkProver使用CIRCOM circuit库 来生成witness for the zk-STARK proof produced by the STARK Recursion Component。【采用CIROM库，生成的witness本质就是以R1CS约束来表达的Arithmetic circuit。】
  • 4）zk-SNARK Prover：为Rapid SNARK，以C++和Intel汇编语言编写，为CIRCOM输出快速生成证明。输入为：CIRCOM生成的witness、STARK verifier data（以表明Rapid SNARK如何处理该数据），输出为：a zk-SNARK proof。


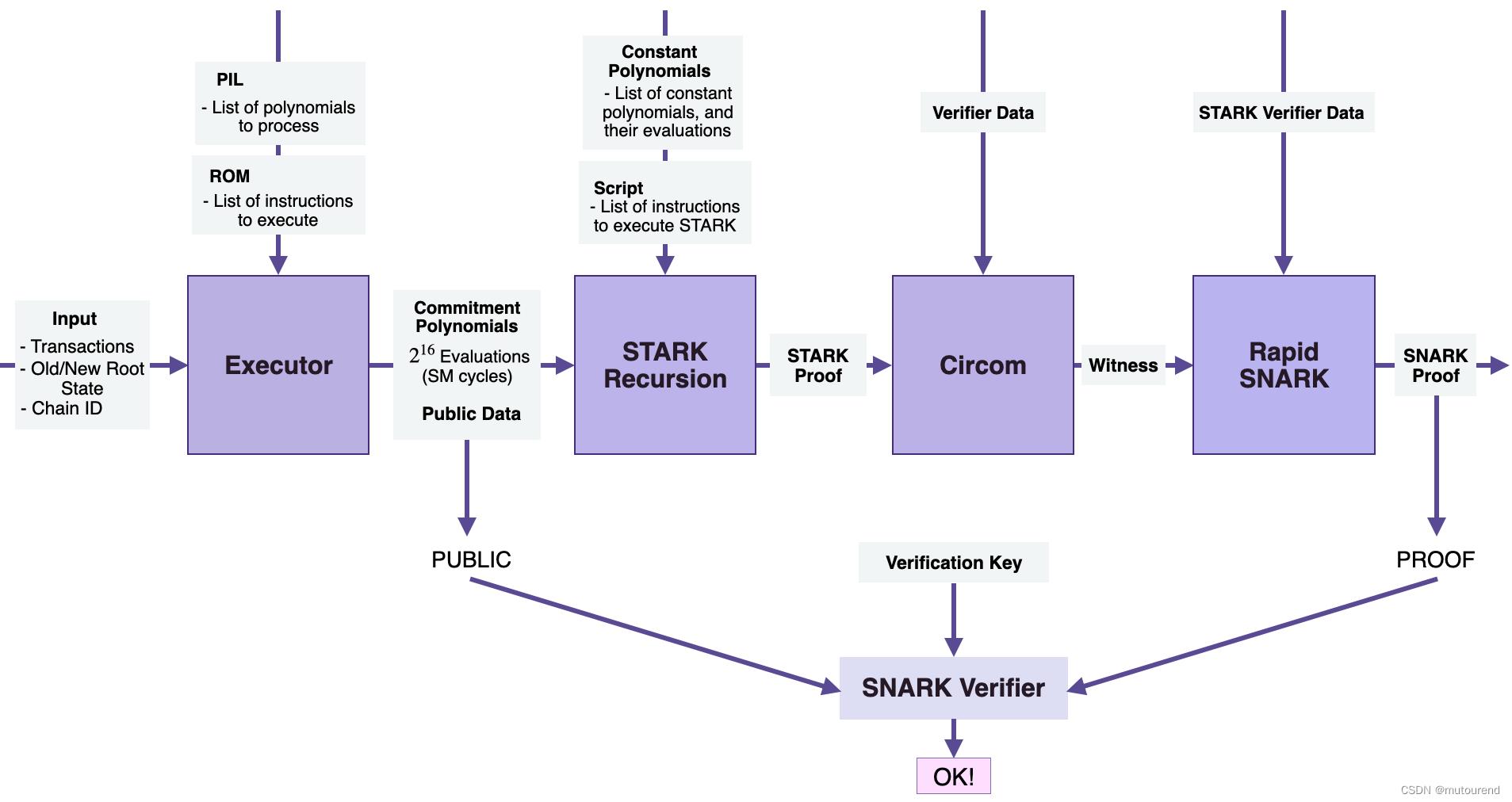
采用zk-STARK是因其证明速度很快，无需trusted setup，但是，zk-STARK的proof size很大，为此，引入zk-SNARK来证明zk-STARK proof的正确性，然后将zk-SNARK proof作为状态变化的validity proof发送到L1。借助zk-SNARK，验证validity proof的gas开销由500万降低为35万。

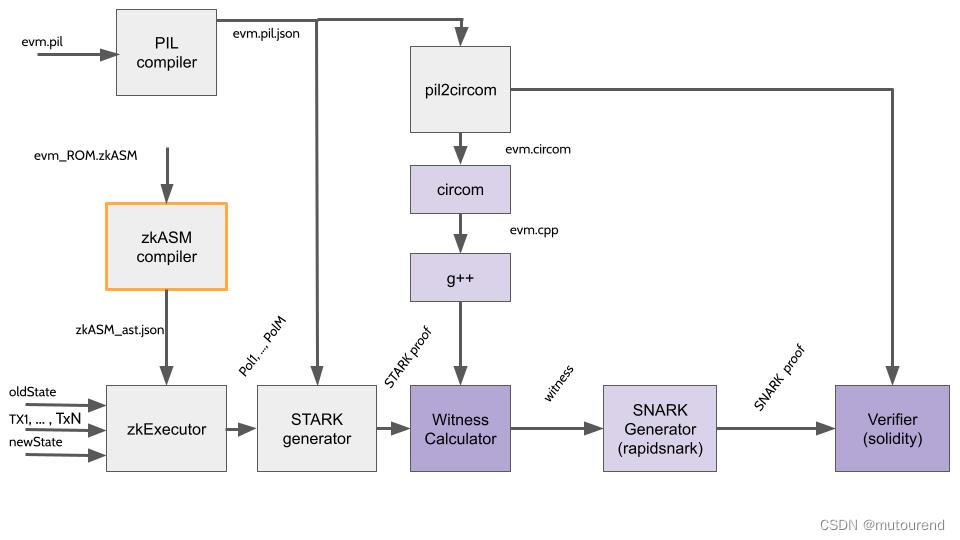
4. Modular Design

对于如EVM这样的复杂state machine，其execution trace对应的列数量和identities数量可达数千。而管理如此庞大的矩阵将是非常复杂且难处理的。

为简化，Polygon zkEVM使用divide and conquer技术，将execution trace切分为更小的矩阵。
使用名为plookup的proving技术，使得一个矩阵的行 可 关联到 另一矩阵的行 成为可能。

此外，还使用了：

  • inclusion：检查某矩阵的行 被包含 在另一矩阵中。
  • permutation：检查某矩阵中的行 与 另一矩阵中的行 相同，只是顺序不同。

PIL语言：

  • 使用namespace关键字来命名execution trace中切分的每个矩阵的列。
  • 使用in关键字来定义inclusion。
  • 使用is关键字来定义permutation。

Polygon zkEVM中，会将execution trace切分为：

  • 一个主矩阵：又名main state machine。
  • 多个二级矩阵：又名secondary state machine。

借助divide and conquer技术：

  • Polygon zkEVM中包含了不同的connected state machine。
  • 每个state machine致力于证明某特定task的execution。
  • 不同state machines之间的相关列（polynomials）使用inclusion proof（with plookup）来关联。

5. 一个例子——Fibonacci state machine

Fibonacci序列： a 1 , a 2 , … , a n \\mathbfa_1, a_2, \\dots , a_n a1​,a2​,…,an​，满足 a i + 1 = a i − 1 + a i \\mathbf a_i+1 = a_i-1 + a_i ai+1​=ai−1​+ai​。

如具有12个成员的序列：
   0 ,    1 ,    1 ,    2 ,    3 ,    5 ,    8 ,    13 ,    21 ,    34 ,    55 ,    89 ,    … \\mathbf \\ \\ 0,\\ \\ 1,\\ \\ 1,\\ \\ 2,\\ \\ 3,\\ \\ 5,\\ \\ 8,\\ \\ 13,\\ \\ 21,\\ \\ 34,\\ \\ 55,\\ \\ 89,\\ \\ \\dots   0,  1,  1,  2,  3,  5,  8,  13,  21,  34,  55,  89,  …
很容易检查发现 377 \\mathbf377 377和 987 \\mathbf987 987是Fibonacci 序列成员。但若要判断 12 , 586 , 269 , 025 \\mathbf 12,586,269,025 12,586,269,025是否为序列成员，则需要一个公式 或 计算机程序——本文以state machine密码学工具来实现。

5.1 Fibonacci State Machine

具有寄存器 A = ( A 1 , A 2 , … , A l ) \\mathbfA = ( A_1, A_2, \\dots , A_l ) A=(A1​,A2​,…,Al​)和 B = ( B 1 , B 2 , … , B l ) \\mathbfB = ( B_1, B_ 2, \\dots , B_l ) B=(B1​,B2​,…,Bl​)的状态机，第 i i i个状态为 ( A i , B i ) (A_i,B_i) (Ai​,Bi​)，初始状态为 A 1 = 0 , B 1 = 1 A_1=0,B_1=1 A1​=0,B1​=1。

A 和 B \\mathbfA和\\mathbfB A和B寄存器均包含了Fibonacci序列，只是 B \\mathbfB B中的序列为one step ahead of A \\mathbfA A，二者具有如下关系：
A i + 1 = B i , B i + 1 = A i + B i . \\beginaligned A_i+1 &= B_i , \\\\ B_i+1 &= A_i + B_i. \\endaligned Ai+1​Bi+1​​=Bi​,=Ai​+Bi​.​
接下来，是将这些寄存器以多项式表示，并最终引入多项式承诺机制来构建该membership密码学工具。

5.1.1 polynomial identities

区块链传统中，将2个寄存器的多项式表示为 Z p [ x ] \\mathbbZ_p[x] Zp​[x]，其系数源自a prime field Z p \\mathbbZ_p Zp​。
将多项式evaluate over subgroup of H = ω , ω 2 , ω 3 , … , ω 8 = 1 = ⟨ ω ⟩ H = \\\\omega,\\omega^2,\\omega^3,\\dots,\\omega^8 = 1\\ = \\langle\\omega\\rangle H=ω,ω2,ω3,…,ω8=1=⟨ω⟩ of order 8 8 8。
定义多项式 P ( x ) P(x) P(x)和 Q ( x ) Q(x) Q(x)为：
P ( ω i ) = A i , Q ( ω i ) = B i . P(\\omega^i) = A_i, \\\\ Q(\\omega^i) = B_i. P(ωi)=Ai​,Q(ωi)=Bi​.

H H H中的每个 x x x形式为 x = ω i x=\\omega^i x=ωi for some i i i，从而有：
P ( x ω ) = P ( ω i + 1 ) = A i + 1 , Q ( x ω ) = Q ( ω i + 1 ) = B i + 1 . \\beginaligned P(x\\omega) &= P(\\omega^i + 1) = A_i+1, \\\\ Q(x\\omega) &= Q(\\omega^i+1) = B_i+1. \\endaligned P(xω)Q(xω)​<

以上是关于Polygon zkEVM 基本概念的主要内容，如果未能解决你的问题，请参考以下文章

Polygon zkEVM工具——PIL和CIRCOM

Polygon zkEVM的pil-stark Fibonacci状态机初体验

Polygon zkEVM——Hermez 2.0简介

Polygon zkEVM zkROM代码解析

Polygon zkEVM zkROM代码解析

Polygon zkEVM zkROM代码解析