单目标优化求解基于matlab增强型黑猩猩优化器算法求解单目标优化问题含Matlab源码 2013期
Posted 海神之光
tags:
篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了单目标优化求解基于matlab增强型黑猩猩优化器算法求解单目标优化问题含Matlab源码 2013期相关的知识，希望对你有一定的参考价值。
一、黑猩猩优化算法(ChOA)简介
1 ChOA数学描述
黑猩猩优化算法(ChOA) 是M.Khi she等人于2020年根据黑猩猩群体狩猎行为提出的一种新型元启发式优化算法。ChOA通过模拟攻击黑猩猩、驱赶黑猩猩、拦截黑猩猩和追逐黑猩猩4类黑猩猩协同狩猎行为来达到求解问题的目的。与其他算法相比， ChOA具有收敛速度快、寻优精度高等特点。
(1)驱赶和追逐猎物。
在黑猩猩狩猎过程中，通常根据黑猩猩个体智力和性动机来分配狩猎职责。任何黑猩猩均可随机改变其在猎物周围空间中的位置，数学描述为
d=|cx prey(t) -mx chimp(t) |(1)
x chimp(t+1) =X prey(t) -ad(2)
式中：d为黑猩猩与猎物间距； t为当前迭代次数； X prey(t) 为猎物位置向量； X chimp(t) 为黑猩猩位置向量； a、m、c为系数向量， a=2fr 1-f， c=2r 2， m=Chaotic_value(基于混沌映射的混沌向量) ， f为迭代过程中从2.0非线性降至0， r 1、r 2为[0， 1] 范围内的随机向量。
(2)攻击方式。
黑猩猩能够探查猎物位置(通过驱赶、拦截和追逐),然后包围猎物。狩猎过程通常由攻击黑猩猩进行,驱赶黑猩猩、拦截黑猩猩和追逐黑猩猩参与狩猎过程。4类黑猩猩通过下式更新其位置,其他黑猩猩根据最佳黑猩猩位置更新其位置,猎物位置由最佳黑猩猩个体位置估计。数学描述为
式中:dAttacker、dBarrier、dChaser、dDriver分别为当前攻击黑猩猩、拦截黑猩猩、追逐黑猩猩、驱赶黑猩猩与猎物的间距;xAttacker、xBarrier、xChaser、xDriver分别为攻击黑猩猩、拦截黑猩猩、追逐黑猩猩、驱赶黑猩猩相对于猎物的位置向量;a1～a4、m1～m4、c1～c4分别为攻击黑猩猩、拦截黑猩猩、追逐黑猩猩、驱赶黑猩猩系数向量;x1、x2、x3、x4分别为攻击黑猩猩、拦截黑猩猩、追逐黑猩猩和驱赶黑猩猩位置更新向量;x为其他黑猩猩位置向量。
(3)攻击和寻找猎物。
在狩猎最后阶段,一方面黑猩猩根据攻击者、驱赶者、拦截者和追逐者位置更新位置,并攻击猎物;另一方面黑猩猩通过分散寻找猎物显示探查过程,即ChOA全局搜索。
(4)社会动机。
社会动机(性爱和修饰)会导致黑猩猩放弃其狩猎职责,这一行为有助于ChOA在求解高维问题时克服陷入局部最优和收敛速度慢等缺点。在优化过程中,通过50%的概率选择黑猩猩正常位置更新或通过混沌模型进行位置更新。数学模型表示为
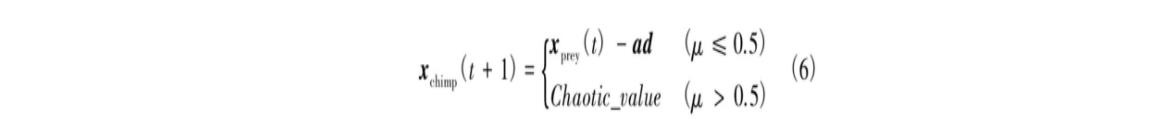
式中:μ为[0,1]范围内的随机数。
二、部分源代码
close all
clear
clc
Algorithm_Name = 'I-ChoA';
N = 30; % Number of search agents
SearchAgents_no =N;
Function_name='F2'; % Name of the test function that can be from F1 to F23 (Table 1,2,3 in the paper)
Max_iteration = 500; % Maximum numbef of iterations
% Load details of the selected benchmark function
[lb,ub,dim,fobj]=Get_Functions_details(Function_name);
[ABest_scoreChimp1,ABest_posChimp1,IChoA_curve]=IChoA(SearchAgents_no,Max_iteration,lb,ub,dim,fobj);
figure('Position',[500 500 660 290])
%Draw search space
subplot(1,2,1);
func_plot(Function_name);
title('Parameter space')
xlabel('x_1');
ylabel('x_2');
zlabel([Function_name,'( x_1 , x_2 )'])
%Draw objective space
subplot(1,2,2);
semilogy(IChoA_curve,'Color','r')
title('Objective space')
xlabel('Iteration');
ylabel('Best score obtained so far');
axis tight
grid on
box on
legend('I-ChoA')
function [Attacker_score,Attacker_pos,Convergence_curve]=IChoA(N,Max_iter,lb,ub,dim,fobj)
% initialize Attacker, Barrier, Chaser, and Driver
Attacker_pos=zeros(1,dim);
Attacker_score=inf; %change this to -inf for maximization problems
Barrier_pos=zeros(1,dim);
Barrier_score=inf; %change this to -inf for maximization problems
Chaser_pos=zeros(1,dim);
Chaser_score=inf; %change this to -inf for maximization problems
Driver_pos=zeros(1,dim);
Driver_score=inf; %change this to -inf for maximization problems
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
lu = [lb .* ones(1, dim); ub .* ones(1, dim)]; %% =========
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%Initialize the positions of search agents
Positions=initialization(N,dim,ub,lb);
%============================================================
Positions = boundConstraint (Positions, Positions, lu); %% =====
% Calculate objective function for each champ
for i=1:size(Positions,1)
Fit(i) = fobj(Positions(i,:));
end
% Personal best fitness and position obtained by each champ
pBestScore = Fit;
pBest = Positions;
neighbor = zeros(N,N);
%%=======================================================================
Convergence_curve=zeros(1,Max_iter);
l=0;% Loop counter
%%
% Main loop
while l<Max_iter
for i=1:size(Positions,1)
%%=========================================
fitness = Fit(i);
% Update Attacker, Barrier, Chaser, and Driver
if fitness<Attacker_score
Attacker_score=fitness; % Update Attacker
Attacker_pos=Positions(i,:);
end
if fitness>Attacker_score && fitness<Barrier_score
Barrier_score=fitness; % Update Barrier
Barrier_pos=Positions(i,:);
end
if fitness>Attacker_score && fitness>Barrier_score && fitness<Chaser_score
Chaser_score=fitness; % Update Chaser
Chaser_pos=Positions(i,:);
end
if fitness>Attacker_score && fitness>Barrier_score && fitness>Chaser_score && fitness>Driver_score
Driver_score=fitness; % Update Driver
Driver_pos=Positions(i,:);
end
end
f=2-l*((2)/Max_iter); % a decreases linearly fron 2 to 0
% The Dynamic Coefficient of f Vector as Table 1.
%Group 1
C1G1=1.95-((2*l^(1/3))/(Max_iter^(1/3)));
C2G1=(2*l^(1/3))/(Max_iter^(1/3))+0.5;
%Group 2
C1G2= 1.95-((2*l^(1/3))/(Max_iter^(1/3)));
C2G2=(2*(l^3)/(Max_iter^3))+0.5;
%Group 3
C1G3=(-2*(l^3)/(Max_iter^3))+2.5;
C2G3=(2*l^(1/3))/(Max_iter^(1/3))+0.5;
%Group 4
C1G4=(-2*(l^3)/(Max_iter^3))+2.5;
C2G4=(2*(l^3)/(Max_iter^3))+0.5;
% Update the Position of search agents including omegas
for i=1:size(Positions,1)
for j=1:size(Positions,2)
%
%
%% Please note that to choose a other groups you should use the related group strategies
r11=C1G1*rand(); % r1 is a random number in [0,1]
r12=C2G1*rand(); % r2 is a random number in [0,1]
r21=C1G2*rand(); % r1 is a random number in [0,1]
r22=C2G2*rand(); % r2 is a random number in [0,1]
r31=C1G3*rand(); % r1 is a random number in [0,1]
r32=C2G3*rand(); % r2 is a random number in [0,1]
r41=C1G4*rand(); % r1 is a random number in [0,1]
r42=C2G4*rand(); % r2 is a random number in [0,1]
A1=2*f*r11-f; % Equation (3)
C1=2*r12; % Equation (4)
%% % Please note that to choose various Chaotic maps you should use the related Chaotic maps strategies
m=chaos(3,1,1); % Equation (5)
D_Attacker=abs(C1*Attacker_pos(j)-m*Positions(i,j)); % Equation (6)
X1=Attacker_pos(j)-A1*D_Attacker; % Equation (7)
A2=2*f*r21-f; % Equation (3)
C2=2*r22; % Equation (4)
D_Barrier=abs(C2*Barrier_pos(j)-m*Positions(i,j)); % Equation (6)
X2=Barrier_pos(j)-A2*D_Barrier; % Equation (7)
A3=2*f*r31-f; % Equation (3)
C3=2*r32; % Equation (4)
D_Driver=abs(C3*Chaser_pos(j)-m*Positions(i,j)); % Equation (6)
X3=Chaser_pos(j)-A3*D_Driver; % Equation (7)
A4=2*f*r41-f; % Equation (3)
C4=2*r42; % Equation (4)
D_Driver=abs(C4*Driver_pos(j)-m*Positions(i,j)); % Equation (6)
X4=Chaser_pos(j)-A4*D_Driver; % Equation (7)
X_Chimp(i,j)=(X1+X2+X3+X4)/4;% Equation (8)
end
X_Chimp(i,:) = boundConstraint(X_Chimp(i,:), Positions(i,:), lu);
Fit_Chimp(i) = fobj(X_Chimp(i,:));
end
%% Calculate the candiadate position Xi-DLH
radius = pdist2(Positions, X_Chimp, 'euclidean'); % Equation (10)
dist_Position = squareform(pdist(Positions));
r1 = randperm(N,N);
for t=1:N
neighbor(t,:) = (dist_Position(t,:)<=radius(t,t));
[~,Idx] = find(neighbor(t,:)==1); % Equation (11)
random_Idx_neighbor = randi(size(Idx,2),1,dim);
for d=1:dim
X_DLH(t,d) = Positions(t,d) + rand .*(Positions(Idx(random_Idx_neighbor(d)),d)...
- Positions(r1(t),d)); % Equation (12)
end
X_DLH(t,:) = boundConstraint(X_DLH(t,:), Positions(t,:), lu);
Fit_DLH(t) = fobj(X_DLH(t,:));
end
%% Selection
tmp = Fit_Chimp < Fit_DLH; % Equation (13)
tmp_rep = repmat(tmp',1,dim);
tmpFit = tmp .* Fit_Chimp + (1-tmp) .* Fit_DLH;
tmpPositions = tmp_rep .* X_Chimp + (1-tmp_rep) .* X_DLH;
%% Updating
tmp = pBestScore <= tmpFit; % Equation (13)
tmp_rep = repmat(tmp',1,dim);
pBestScore = tmp .* pBestScore + (1-tmp) .* tmpFit;
pBest = tmp_rep .* pBest + (1-tmp_rep) .* tmpPositions;
Fit = pBestScore;
Positions = pBest;
%%
l = l+1;
neighbor = zeros(N,N);
Convergence_curve(l单目标优化求解 基于matlab加权黑猩猩算法求解单目标问题含Matlab源码 1412期
优化算法基于matlab cubic混沌初始化结合纵横策略正弦余弦算子的黑猩猩优化算法求解单目标优化问题含Matlab源码 2065期
优化算法基于matlab cubic混沌初始化结合纵横策略正弦余弦算子的黑猩猩优化算法求解单目标优化问题含Matlab源码 2065期
单目标优化求解基于matlab平衡算法求解单目标优化问题含Matlab源码 2114期