信息安全技术RSA算法的研究及不同优化策略的比较

Posted 2022-08-06 小镇做题家！

RSA算法的研究及不同优化策略的比较

• 第一章《信息安全技术》课程学习总结
• 第二章 阅读课外资料总结和综述
• • 2.1 基于Python的web黑客攻击技术
  • • 2.1.1 网络钓鱼
    • 2.1.2 域欺骗
    • 2.1.3 SQL注入
    • 2.1.4 Web shell
  • 2.2 云计算安全技术
  • • 2.2.1 可信访问控制
    • 2.2.2 密文检索
    • 2.2.3 可使用性证明与数据存在
    • 2.2.4 虚拟安全技术
• 第三章 RSA算法相关研究
• • 3.1 RSA加密算法原理
  • • 3.1.1 随机生成素数
    • 3.1.2 密钥生成
    • 3.1.3 加密和解密
• 第四章 RSA算法的实现
• • 4.1 产生公钥和私钥
  • • 4.1.1 随机生成两个较大素数
    • 4.1.2 求解整数e
    • 4.1.3 求解整数d
  • 4.2 加密和解密
• 第五章RSA算法的优化
• • 5.1 限制随机数范围
  • 5.2 米勒-拉宾素数测试
  • 5.3 列表选择法
• 第六章测试与分析
• • 6.1 基本功能测试
  • 6.2 不同优化策略的对比分析
• 第七章 收获与体会
• 参考文献

第一章《信息安全技术》课程学习总结

信息安全是指信息网络的硬件、软件及其系统中的数据受到保护，不受偶然的或者恶意的原因而遭到破坏、更改、泄露，系统连续可靠正常地运行，信息服务不中断。信息安全的属性可以从两个层次来看，分别为消息层次和网络层次。从消息层次来看，信息安全的属性包括完整性、保密性、不可否认性、可用性、可控性。其中，机密性、完整性、可用性通常被称为信息安全的CIA。
信息加密技术分为两个阶段，传统加密技术阶段与现代加密技术阶段。传统的加密技术阶段并没有进行复杂的计算,只是设计两张表格、将字母在表格中的位置进行调整进行加密和解密。这就要求发送和接收方在进行信息传输的最初就要知道表格中字母的对应关系通过表格找到相应的信息。传统的加密技术包括替换和位移两种方式。现代加密技术分为对称加密算法和非对称加密算法，对称密码算法是指通信的收发双方使用相同密钥的密码,如DES算法。对称密码算法的优点是只需要一个密码即可，比较简便，缺点则是信息安全性不高。非对称密码算法是指通信的收发双方使用具有两组密钥的密码,如RSA算法。一个作为公钥对外公开,另一个作为私得不对外公开,用来进行解密。
目前信息认证技术涉及身份认证和消息认证两个方面。身份认证技术主要用于鉴别用户的身份是否合法和真实。在真实世界中，验证一个人的身份的主要通过3种方式:一是根据你所知道 的信息来证明身份，二是根据你所拥有的物品来证数明身份，三是直接根据你独无二的身体特征来证明身份。消息认证技术主要用于验证所收到的消息确实是来自真正的发送方且未被修改的消息，它包含两层含义，一是验证信息的发送者是真正的而不是冒充的，二是验证信息在传送过程中未被篡改、重放或延迟等。
信息隐藏又称信息伪装，就是通过减少载体的某种冗余，来隐藏敏感信息，达到某种特殊的目的。信息隐藏技术包括隐写术和数字水印两种技术。隐写术的目的是在不引起任何怀疑的情况下秘密传送信息，因此它的主要要求是不被检测到和大容量等。数字水印技术是指在数字化的数据内容中嵌人不明显的记号。
操作系统安全的主要目标是监督保障系统运行的安全性，保障系统自身的安全性，标识系统中的用户，进行身份认证，依据系统安全策略对用户的操作行为进行监控。数据库安全技术包括数据库加密和数据库备份与恢复。数据加密是对计算机系统外存储器中数据最有效的保护措施之。由于计算机系统中硬件故障、软件错误、操作员失误以及恶意的破坏仍然时有发生，影响数据库中数据的正确性，甚至破坏数据库，此时就要求数据库管理系统必须具有把数据库从错误状态下恢复到正确状态的功能，这就是数据恢复。恢复的基本原理就是利用冗余。
访问控制是信息系统安全防范和保护的主要策略，它的主要任务是保证系统资源不被非法使制的基用和非常规访问。访问控制规定了主体对客体访问的限制，并在身份认证的基础上，对提出资源访问的请求加以控制。当前主要的访问控制策略包括三种：自主访问控制、强制访问控制和基于角色的访问控制。

第二章 阅读课外资料总结和综述

2.1 基于Python的web黑客攻击技术

2.1.1 网络钓鱼

网络钓鱼是指黑客通过精心设计与银行等类似的假冒网站，骗取受害人在这些网站输入的金融信息或个人敏感信息。首先，黑客向用户发送声称来自银行或其他知名机构的期诈性的邮件或链接信息，用户打开电子邮件或点击其中链接，就会进入黑客精心伪造的的鱼网站。在其中输入用户名与密码，假冒网站就会保存用户的这些信息，黑客利用这些输入信息发动更深层次的攻击。

2.1.2 域欺骗

域欺骗攻击中，黑客首先入侵DNS服务器，修改正常的网站域名与IP对照表，将仿冒网站的IP地址发送给用户浏览器，从而将用户引导至精心设计的仿冒网站。这样，用户在这些网站输入的个人信息就会被偷偷盗走，此攻击类似网络钓鱼攻击。不同之处是域欺骗是伪装DNS，用户并不知情。

2.1.3 SQL注入

SQL注入主要利用html input标签发动攻击。首先，浏览器接收用户输入的账号与密码，并将其发送给Web服务器。Web服务器通过SQL语句查询数据库，比对是否存在与输入的账号和密码一致的用户信息。此时，黑客向用户账号与密码中输入的不是正常值，而是一些能够诱使数掘库产生错误行为的值。黑客通过反复输入非正常的SQL语句，并分析数据库返回的数据，从而得到最适合对系统进行攻击的SQL语句,SQL注入攻击在Pyhon的sqlmap模块下只需5步即可完成。分别是第1步搜索URL，第2步寻找漏同，第3步搜索数据表、第4步搜索列，第5步访问数据。

2.1.4 Web shell

Web shell恶意利用了Web提供的文件上传功能。首先，黑客将用于远程操纵服务器的Web shell文件上传到Web服务器，然后找到上传文件所在位置，得到访问Web shell文件的URL地址。然后，通过该URL地址运行Web shell文件，获取可以控制操作系统的超级权限。Web shell攻击利用Python提供的fileupload等模块也比较容易实现。

2.2 云计算安全技术

2.2.1 可信访问控制

密码学方法包括四个方案：一是在密钥生成、分配策略结合的方式进行访问控制。二是利用加密算法方案，比如基于属性加密下的密钥规则或属性加密下的密文规则。三是代理重复加密。四是将访问控制树嵌入到用户重要密文或重要密钥中。在当前,这些方案具有一定的时间授权与约束等。

2.2.2 密文检索

密文检索分为安全索引与密文扫描两种典型方法,前者方法利用密文中较重要词句进行安全索引，索引并查询该重要词句，后者方法是比对密文中的每个词句,确从重要词是否引出,并计算出重要词句出现的次教。密交处理是在同态加密算法的基础上进行研究。

2.2.3 可使用性证明与数据存在

当前大数据的发展导致通信投入巨大代价，用户下载数据后，无法验证其正确性，所以，云用户只有下载数据，才能利用特定协议或分析手段,并通过概率判断用户数据的完整性。其内容包括:云用户进行数据验证时,可利用两种方法进行验证,一是可检索证明方法，二是数据持有证明方法。

2.2.4 虚拟安全技术

云计算平台上的提供者必须保证云用户的数据的隔离性与安全性，研究者研究出隔离执行机，隔离执行机是在虚拟机的grid环境基础上进行开发,通过缓存层次的核心分配、给予缓存划分的页染色,这两种方法具有性能保护与安全隔离的作用。这两种方法可对VM缓存接口进行隔离影响，并将其融入云架构的框架中。

第三章 RSA算法相关研究

3.1 RSA加密算法原理

RSA算法是第一个能同时用于加密和数字签名的算法，也易于理解和操作。近些年来，RSA加密算法不断被黑客攻击，但在许多场景下用户信息安全都得到了保障，体现出较好的保护作用，现已逐步被大众接受。传统的RSA加密算法流程主要包括随机生成素数、密钥生成、加密明文和解密密文。

3.1.1 随机生成素数

通常采用试除法获取RSA加密算法中的随机素数，获取一个随机数x,判断x是否能被2到sqrt(x)间的数整数，如果可以被整除则说明x不是素数。

3.1.2 密钥生成

用于生成密钥生成需要用到密钥对，过程如下：
(1)随机生成两个素数p和q，满足p!=q。
(2)计算出n=q * q,计算出欧拉函数ψ(n)=(p-1) * (q-1)。
(3)随机生成正整数e，要求满足1<e<ψ(n)，且与ψ(n)互质。
(4)计算得到d，e * d (modψ(n))。
(5)得到密钥对，其中公钥为(e,n),私钥为(d,n)。

3.1.3 加密和解密

对原始数据处理获取密文的过程定义为加密，加密计算公式为。其中M为原始数据，(e,n)为传输给用户的公钥，C为加密后的得到的密文。
利用私钥解开密文得到原始数据的过程定义为解密，解密计算公式为。其中C为回传的密文，(d,n)为私钥，M为解密后的得到的原始数据。

第四章 RSA算法的实现

4.1 产生公钥和私钥

4.1.1 随机生成两个较大素数

找到两个大素数是整个RSA算法中最慢的步骤之一，这里先采用的方法是不断的生成随机数，直到找到符合要求的素数为止。首先，需要能够判断一个数是否为素数，最简单的方法就是看这个数是否有除了1和它本身以外的其他因数，即试除法。检测素数的代码段如下。

//试除法判定素数
bool is_prime(ll x)

	for (ll i=2;i<sqrt(x);i++)
		if(x%i==0)return false;
	return true;

检测素数以后，就可以进行较大素数的生成。为了达到“较大“的要求，我只对大于100的数进行筛选，实现的主要代码如下。为防止过慢，这里的get_random()只生成小于200的随机数。

//随机数生成
ll get_random()

    ll num;
    //time()用系统时间初始化种,为rand()生成不同的随机种子
    srand((int)time(0));
    num=rand()%200;
    return num;

 // 随机生成符合条件的p,q
    while(1)
	while(1)
	p=get_random();              //得到随机数
	if(p>100&&is_prime(p))break;	//条件为大于100的素数
	
	while(1)
	q=get_random();			//得到第二个随机数
	if(q>100&&is_prime(q))break;//条件为大于100的素数
	
	if(p!=q)                  //两个数不能相同
	cout<<"p="<< p<< ",q=" <<q<<endl;//得到两个大素数
            break;
	 

得到两个素数p和q后,即可计算n=p * q,ψ(n)=(p-1) * (q-1)。

4.1.2 求解整数e

为了得到一个与ψ(n)互质的整数e，首先需要能够计算两个数的最大公约数，最大公约数为1即为互质。我使用辗转取余法求最大公约数。主要代码如下。

//辗转取余法求最大公约数
ll divisor(ll x,ll y)

	int temp;
	while (y)
    
      temp=x;
		 x=y;
		 y=temp%y;
	
	return x; 

判断两个数是否互质以后，通过循环随机取数，找到符合条件的e，代码如下。为了加快速度，这里的get_random()仍然取的是200以下的随机数。

 // 随机生成符合条件的e
   while(1)
	
		e=get_random();
		if(divisor(e, eular)==1&&e>1&&e<eular)
         break;
	

4.1.3 求解整数d

为了得到一个整数d，使得e * d 求余ψ(n) 的余数为 1，可以从1开始寻找一个整数i，当整数i满足条件时，可将该值赋给d，这样也能保证找到的d尽量的小，加快程序速度。主要代码段如下。

//计算私钥d
ll get_d(ll e,ll eular)

    for(ll i=1;;i++)
        if((e*i)%eular==1)return i;

4.2 加密和解密

在RSA中，加密和解密的过程使用了费尔马小定理的两种等价的描述。简单来说，对明文M进行加密求得密文C的公式为。公式看起来不难，但在具体实现中遇到了一些问题。因为e的值通常是三位数，导致a^e的数值太大，就算是使用C++中long long类型也会造成溢出，所以我根据求余运算的分配律进行等价的迭代计算，这样，就把一次性的幂运算分成了多次较小数的求余计算，避免了出现溢出的情况。分配律公式为 。本问题中a和b的值是相同的，主要代码如下。这里的text即为保存明文的数组。

   for(int i=0;i<10;i++)
    ll temp=text[i]%n;       //保存a对n求余的值
	for(int j=0;j<e-1;j++) //迭代求余
	text[i]=(temp*(text[i]%n))%n;
	
      cout<<text[i]<<" ";
	

对密文C，解密求得明文M的公式为。同样利用分配律进行迭代计算，主要代码与上文的加密类似，text为保存密文的数组，代码如下所示。

for(int i=0;i<10;i++)
    ll temp1=text[i]%n;        //保存a对n求余的值
	for (int j=0;j <d-1;j++) //迭代求余
	text[i]=(temp1*(text[i]%n))%n;
	
		cout<<text[i]<<" ";
	

第五章RSA算法的优化

在实际测试中，我发现程序运行的非常慢，尤其是产生素数的部分，这里慢的最主要的原因是素数的检测太慢。所以我对如何加快素数的生成进行以下研究。

5.1 限制随机数范围

在生成素数时，我之前使用的方法是随机产生一个数然后再判断是否其达到条件，导致效率很慢。既然在筛选的条件之一是保证其“较大”，还不如直接生成一个较大区间内的随机数，比如我设置的是100到200之间的随机数，这样避免了很多无效的生成。改变后的代码如下。

ll get_random()

    ll num;
    //time()用系统时间初始化种,为rand()生成不同的随机种子
    srand((int)time(0));
    return 100+rand()%100;

之后，对其筛选条件进行更改，只需判断是否为素数。

5.2 米勒-拉宾素数测试

在网上查询资料后，我发现一种叫米勒-拉宾的快速测试素数的方法，这是一种基于概率的非确定性素数判定法，正确率非常高，我感觉应该可以应用于RSA算法当中。该算法的原理，首先确定几个基底a,范围在[2,n-1]，当有一个数n，先判断是不是2，3的倍数，是则不为素数。若不是则为一个奇数，继续，令n-1=(2^r) * d，取不同的a，对r从0到最大，满足ad≡1(mod n)，此处分以下情况，d为奇数，若同余1，可能为质数。d为偶数，若同余-1，可能为质数。循环后不符合上述情况，必为合数。主要代码如下。

bool MRprime(ll a,ll n)
	ll r=0,b=n-1;
	if (!(n%a)) return false;	//倍数必为合数
	while(!(b&1))			//找到奇数
	
		b>>=1;
		r++;
	
	ll k=qmi(a,b,n);
	if(k==1) return true;	//同余1
	for(int i=0;i<r;i++,k=k*k%n)
		if(k==n-1) return true;	//同余-1
	return false;

bool CheckPrime(int n)

	if(n==2||n==3||n==7||n==61)return true;
	if(!(n&1)||n%3==0)return false;
	if(MRprime(2,n)&&MRprime(7,n)&& MRprime(61,n)) return true;
	return false;

5.3 列表选择法

因为本文的程序中的大素数仅仅为在一定区间内的三位数，采用列表选择法肯定是最有效的，找出得到100到200之间的素数，在生成素数时，在以上列表中随机取一个数即可，直接省去了检测。可以预见这种方法肯定是最快的，而且区间设置再扩大几倍也基本没有影响。

第六章测试与分析

6.1 基本功能测试

随机给出一组明文测试数据：11,123,345,456,57,689,777,87,926,1111。使用原始方法进行加密和解密测试，结果如图1所示。

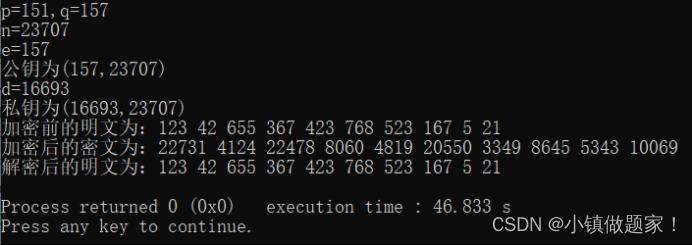
图1 原始方法测试结果
由图1可见，程序的基本功能已经完成。

6.2 不同优化策略的对比分析

对上述同一组数据分别使用限制随机数范围、米勒-拉宾素数测试、列表选择法进行加密和解密测试，结果分别如图2,3,4所示。

图2 限制随机数范围测试结果

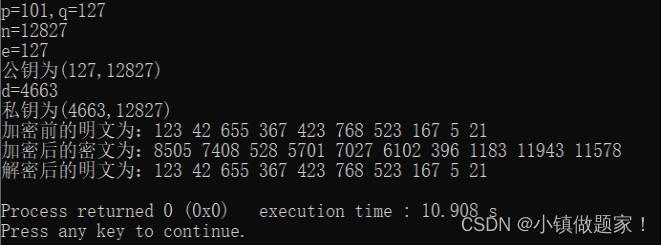
图3 米勒-拉宾素数测试结果

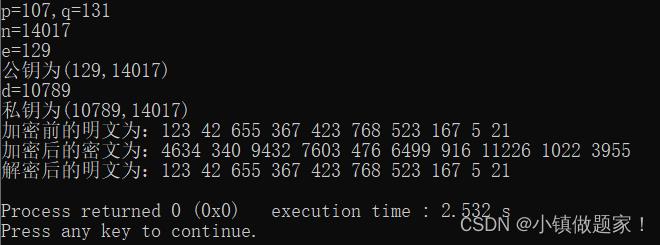
图4 列表选择法测试结果
随后分别对原始方法、限制随机数范围、米勒-拉宾测试、列表选择法四种不同的方法进行十次计时测试，并进行对比分析，四种测试结果如下表1所示。
表1 四种方法测试结果(单位：秒)

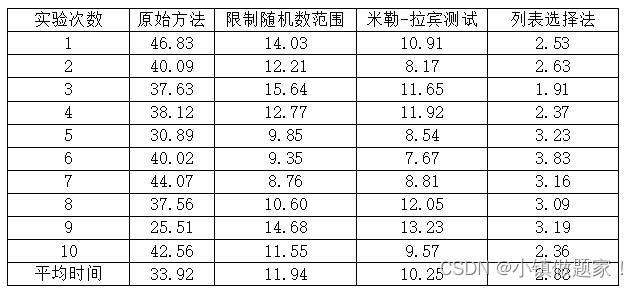
可以看到原始的方法是非常慢的，限制随机数范围可以提高速度，而使用米勒-拉宾测试并没有起到太大的作用，可能只稍微提高速度，列表选择法就像预测的一样，是最快的方法。
但是，由RSA的机制可以想到，如果限制了随机数的范围，则生成素数的范围也被限制，这样破译密钥的复杂度也降低了，因为分解因子时不再盲目，而是可以有范围的穷举。所以我认为这种降低可靠性的方法肯定是不能正式使用的。而用素数列表直接选择素数的方法在要生成1024或2048(二进制)位数的情况下也是不现实的，需要存储数据的容量太大。而米勒-拉宾测试法虽然在本文的实验中看起来效果不明显，但对于大型数据应该具有较好的优势，因为当数据的量级变大时，用试除法的所花的时间是指数级上升的，而米勒-拉宾测试受到的影响相较起来较小。

第七章 收获与体会

通过本学期对《信息安全概论》的学习以及课外文献的阅读，学生我在对于传统的RSA算法的原理进行了研究并且深刻理解了RSA算法基本原理。上述文章介绍了RSA 算法所涉及到的密码学基础概念，在此基础上,分析了RSA 算法的基本原理,详细设计了RSA算法实现的各个子模块,并采用C++语言简单实现，RSA算法不仅可以用于加密解密,还可用于数字签名以及交换对称加密算法的密钥等方面的应用。
RSA加密算法作为非对称加密算法,能够提高信息安全性,为数字时代的发展提供可靠的保障。但由于其运算量大,存在效率低的不足,如果对RSA算法进行优化,能够使信息保护的措施会更加先进和完善。通过限制随机数范围、米勒-拉宾测试、列表选择法，三种不同的优化策略进行实验测试对比，米勒-拉宾测试法虽然在本文的实验中看起来效果不明显，但对于大型数据应该具有较好的优势，所以，使用米勒-拉宾测试可以更好的提高RSA算法的效率。
大数据时代，计算机网络在给人们的生活带来高效和便捷的同时，也存在众多网络安全间题，黑客攻击就是网络安全的主要威时和防御难度最大的环节之一。有效防范治理黑客攻击行为，保障计算机网络数据信息安全，为人们创建安全健康的网络环境。

参考文献

[1]汪林.云计算时代数据安全防护策略.电子元器件与信息技术,2021,5(08):137-138.
[2]金元浦.大数据时代个人隐私泄露的调研分析.清华大学学报,2021,36(01):65-67.
[3]邱晓鹏.基于Python应用程序黑客攻击分析实施.办公自动化,2021,26(19):55-57.
[4]贺军忠.基于Python的WEB黑客攻击技术分析研究.软件工程,2020,23(06):33-35.
[5]董颖.大数据时代网络黑客攻击与防范治理.网络安全技术与应用,2021(05):68-70.
[6]邹震.云计算安全研究.中国设备工程,2019(16):229-230.
[7]祝珂,雷冰冰.改进的RSA加密算法设计与实现.科技技术创新,2021(17):98-99.
[8]张华.RSA算法对信息保护的意义和作用.科技风,2018(31):78-79.
[9]戈改珍.RSA算法的研究与实现.现代计算机(专业版),2018(30):12-14.
[10]李峰,顾申,高鹏.快速素数生成方法综述.密码学报,2019,6(04):463-476.