matlab求解单配送中心多车辆tsp路径优化问题mtspf_ga

Posted 2022-08-03 张叔zhangshu

代码

function varargout = mtspf_ga(xy,dmat,salesmen,min_tour,pop_size,num_iter,show_prog,show_res)

nargs = 8;
for k = nargin:nargs-1
    switch k
        case 0
%             xy = 10*rand(40,2);
xy=[50,50;11,23;21,59;23,21;62,71;67,64;90,66;70,55;63,22;87,46;55,19;93,8;69,12;12,98;20,81;42,88;44,63;31,74];
        case 1
            N = size(xy,1);
            a = meshgrid(1:N);
            dmat = reshape(sqrt(sum((xy(a,:)-xy(a',:)).^2,2)),N,N);
        case 2
            salesmen = 4;
        case 3
            min_tour = 2;
        case 4
            pop_size = 80;
        case 5
            num_iter = 5e3;
        case 6
            show_prog = 1;
        case 7
            show_res = 1;
        otherwise
    end
end
%%
% Verify Inputs
[N,dims] = size(xy);
[nr,nc] = size(dmat);
if N ~= nr || N ~= nc
    error('Invalid XY or DMAT inputs!')
end
n = N - 1; % Separate Start/End City

% Sanity Checks
salesmen = max(1,min(n,round(real(salesmen(1)))));
min_tour = max(1,min(floor(n/salesmen),round(real(min_tour(1)))));
pop_size = max(8,8*ceil(pop_size(1)/8));
num_iter = max(1,round(real(num_iter(1))));
show_prog = logical(show_prog(1));
show_res = logical(show_res(1));

% Initializations for Route Break Point Selection
num_brks = salesmen-1;
dof = n - min_tour*salesmen;          % degrees of freedom
addto = ones(1,dof+1);
for k = 2:num_brks
    addto = cumsum(addto);
end
cum_prob = cumsum(addto)/sum(addto);

% Initialize the Populations
pop_rte = zeros(pop_size,n);          % population of routes
pop_brk = zeros(pop_size,num_brks);   % population of breaks
for k = 1:pop_size
    pop_rte(k,:) = randperm(n)+1;
    pop_brk(k,:) = randbreaks();
end

% Select the Colors for the Plotted Routes
clr = [1 0 0; 0 0 1; 0.67 0 1; 0 1 0; 1 0.5 0];
if salesmen > 5
    clr = hsv(salesmen);
end

% Run the GA
global_min = Inf;
total_dist = zeros(1,pop_size);
dist_history = zeros(1,num_iter);
tmp_pop_rte = zeros(8,n);
tmp_pop_brk = zeros(8,num_brks);
new_pop_rte = zeros(pop_size,n);
new_pop_brk = zeros(pop_size,num_brks);
if show_prog
    pfig = figure('Name','MTSPF_GA | Current Best Solution','Numbertitle','off');
end
for iter = 1:num_iter
    % Evaluate Members of the Population
    for p = 1:pop_size
        d = 0;
        p_rte = pop_rte(p,:);
        p_brk = pop_brk(p,:);
        rng = [[1 p_brk+1];[p_brk n]]';
        for s = 1:salesmen
            d = d + dmat(1,p_rte(rng(s,1))); % Add Start Distance
            for k = rng(s,1):rng(s,2)-1
                d = d + dmat(p_rte(k),p_rte(k+1));
            end
            d = d + dmat(p_rte(rng(s,2)),1); % Add End Distance
        end
        total_dist(p) = d;
    end

    % Find the Best Route in the Population
    [min_dist,index] = min(total_dist);
    dist_history(iter) = min_dist;
    if min_dist < global_min
        global_min = min_dist;
        opt_rte = pop_rte(index,:);
        opt_brk = pop_brk(index,:);
        rng = [[1 opt_brk+1];[opt_brk n]]';
        if show_prog
            % Plot the Best Route
            figure(pfig);
            for s = 1:salesmen
                rte = [1 opt_rte(rng(s,1):rng(s,2)) 1];
                if dims == 3, plot3(xy(rte,1),xy(rte,2),xy(rte,3),'.-','Color',clr(s,:));
                else plot(xy(rte,1),xy(rte,2),'.-','Color',clr(s,:)); end
                title(sprintf('Total Distance = %1.4f, Iteration = %d',min_dist,iter));
                hold on
            end
            if dims == 3, plot3(xy(1,1),xy(1,2),xy(1,3),'ko');
            else plot(xy(1,1),xy(1,2),'ko'); end
            hold off
        end
    end

    % Genetic Algorithm Operators
    rand_grouping = randperm(pop_size);
    for p = 8:8:pop_size
        rtes = pop_rte(rand_grouping(p-7:p),:);
        brks = pop_brk(rand_grouping(p-7:p),:);
        dists = total_dist(rand_grouping(p-7:p));
        [ignore,idx] = min(dists);
        best_of_8_rte = rtes(idx,:);
        best_of_8_brk = brks(idx,:);
        rte_ins_pts = sort(ceil(n*rand(1,2)));
        I = rte_ins_pts(1);
        J = rte_ins_pts(2);
        for k = 1:8 % Generate New Solutions
            tmp_pop_rte(k,:) = best_of_8_rte;
            tmp_pop_brk(k,:) = best_of_8_brk;
            switch k
                case 2 % Flip
                    tmp_pop_rte(k,I:J) = fliplr(tmp_pop_rte(k,I:J));
                case 3 % Swap
                    tmp_pop_rte(k,[I J]) = tmp_pop_rte(k,[J I]);
                case 4 % Slide
                    tmp_pop_rte(k,I:J) = tmp_pop_rte(k,[I+1:J I]);
                case 5 % Modify Breaks
                    tmp_pop_brk(k,:) = randbreaks();
                case 6 % Flip, Modify Breaks
                    tmp_pop_rte(k,I:J) = fliplr(tmp_pop_rte(k,I:J));
                    tmp_pop_brk(k,:) = randbreaks();
                case 7 % Swap, Modify Breaks
                    tmp_pop_rte(k,[I J]) = tmp_pop_rte(k,[J I]);
                    tmp_pop_brk(k,:) = randbreaks();
                case 8 % Slide, Modify Breaks
                    tmp_pop_rte(k,I:J) = tmp_pop_rte(k,[I+1:J I]);
                    tmp_pop_brk(k,:) = randbreaks();
                otherwise % Do Nothing
            end
        end
        new_pop_rte(p-7:p,:) = tmp_pop_rte;
        new_pop_brk(p-7:p,:) = tmp_pop_brk;
    end
    pop_rte = new_pop_rte;
    pop_brk = new_pop_brk;
end

if show_res
    % Plots
    figure('Name','MTSPF_GA | Results','Numbertitle','off');
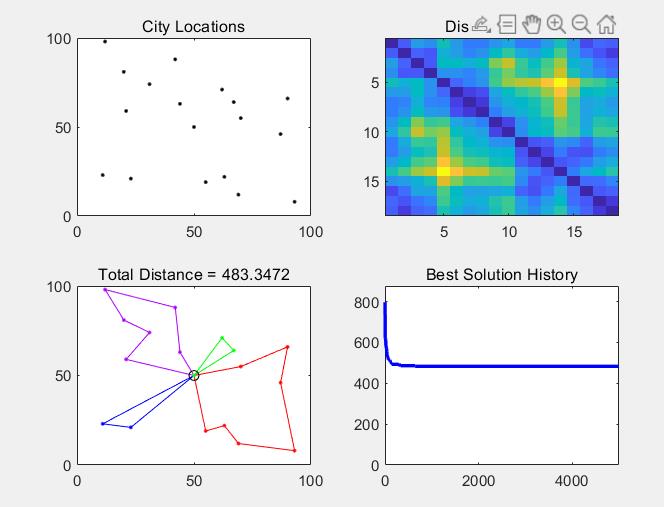
    subplot(2,2,1);
    if dims == 3, plot3(xy(:,1),xy(:,2),xy(:,3),'k.');
    else plot(xy(:,1),xy(:,2),'k.'); end
    title('City Locations');
    subplot(2,2,2);
    imagesc(dmat([1 opt_rte],[1 opt_rte]));
    title('Distance Matrix');
    subplot(2,2,3);
    rng = [[1 opt_brk+1];[opt_brk n]]';
    for s = 1:salesmen
        rte = [1 opt_rte(rng(s,1):rng(s,2)) 1];
        if dims == 3, plot3(xy(rte,1),xy(rte,2),xy(rte,3),'.-','Color',clr(s,:));
        else plot(xy(rte,1),xy(rte,2),'.-','Color',clr(s,:)); end
        title(sprintf('Total Distance = %1.4f',min_dist));
        hold on;
    end
    if dims == 3, plot3(xy(1,1),xy(1,2),xy(1,3),'ko');
    else plot(xy(1,1),xy(1,2),'ko'); end
    subplot(2,2,4);
    plot(dist_history,'b','LineWidth',2);
    title('Best Solution History');
    set(gca,'XLim',[0 num_iter+1],'YLim',[0 1.1*max([1 dist_history])]);
end

% Return Outputs
if nargout
    varargout1 = opt_rte;
    varargout2 = opt_brk;
    varargout3 = min_dist;
end

    % Generate Random Set of Break Points
    function breaks = randbreaks()
        if min_tour == 1 % No Constraints on Breaks
            tmp_brks = randperm(n-1);
            breaks = sort(tmp_brks(1:num_brks));
        else % Force Breaks to be at Least the Minimum Tour Length
            num_adjust = find(rand < cum_prob,1)-1;
            spaces = ceil(num_brks*rand(1,num_adjust));
            adjust = zeros(1,num_brks);
            for kk = 1:num_brks
                adjust(kk) = sum(spaces == kk);
            end
            breaks = min_tour*(1:num_brks) + cumsum(adjust);
        end
    end
end

如需帮忙VX：zzs1056600403