优化调度基于matlab非支配排序遗传算法求解车辆充电调度优化问题含Matlab源码 2000期

Posted 2022-07-28 海神之光

一、遗传算法简介

由于国内外人民的生活方式和电动汽车主要购买人群的不同，国内外关于车辆充电调度问题研究的侧重点也不尽相同。
我国地大物博，人口众多，交通复杂。主要从以下方面研究：
1、通过经济手段或技术手段控制电动汽车的充电时间和充电功率，减小电网峰谷差；
2、考虑全天各时段电价的不同，建立分时电价充电调度系统，减少充电费用；
3、考虑充电桩数量较少且分步不均匀的现状，研究充电设施选址问题；
4、建立虚拟充电站控制中心；
国外地广人稀，主要居住方式与中国也不相同，研究内容如下：
1、设计有多个充电端口的电动汽车充电器，可同时为N辆电动汽车充电；
2、研究混合动力汽车的网络化和供需规划问题；

1 问题描述
本文研究多辆电动汽车的充电调度问题，考虑某时段区域范围内有M 辆电动汽车发出充电请求时，周围有N 个充电桩可以提供充电位的调度情况。把当前调度时段电动汽车和充电桩的基本数据加载到调度中心，调度中心根据电动汽车的当前位置、电量剩余情况和周围充电桩的充电情况进行调度，电动汽车按照最优调度方案到充电桩充电。

充电调度模型考虑优化4个性能指标，分别为：
电动汽车充电时长：包括驾驶时间、充电时间和等待时间；
电动汽车充电费用：包括停车费用和充电费用。
充电桩利用率偏差：避免多辆电动汽车挤占某些充电桩，使其余充电站空闲。造成资源浪费和过渡损耗。
电网平均负载： 避免加重电网负载，维护电网安全

2 充电调度模型

3 群智能优化算法
群智能优化算法是指建立在生物智能或物理现象基础上的随机搜索算法，虽然在理论上不如传统优化算法完善，不能确保解的最优性。但是实际应用过程中，因为对计算中数据的不确定性有很强的适应能力，可以用来求解一些非线性问题，甚至没有确切解析表达式的问题。
本文的车辆充电调度问题是一个多目标优化非线性问题，可以用群智能优化算法来解决。因为每种调度方案都是一个M 行N 列的矩阵，为了解决智能体的构造问题，本文采用基于精英选择的遗传算法和非支配排序遗传算法求解问题，相比其他群智能优化算法，可以更方便的结合问题。

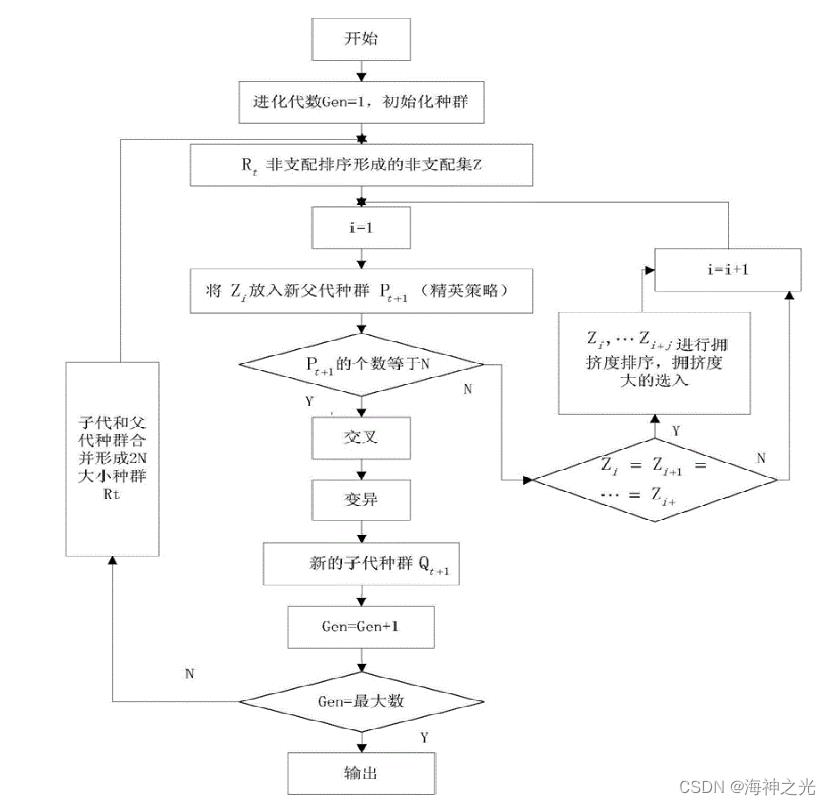
4 非支配排序算法
1）设置种群参数：
2）加载基础数据：加载电动汽车和充电桩的基础数据；
3）初始化种群：生成初始种群个体；
4）交叉、变异：进行交叉和变异操作，生成新的种群；
5）种群合并：进行越界处理，把进行变异操作之后生成的种群和初始种群合并生成新的种群；
6）计算目标函数适应值：计算4个优化目标的适应值；
7）非支配排序：根据种群个体各个优化目标的适应值进行非支配排序；
8）计算拥挤度、选出下一代个体：计算种群个体的拥挤距离，按照拥挤度排序生成下一代种群个体；
9）程序输出：生成Perato解集散点图

Pareto非支配解的概念：
在进行多目标优化时，一个解在某个优化目标最好，而在其他优化目标上比较差即为非支配解。改进一个非支配解的任何目标函数，必然会削弱至少一项其他目标函数。

该算法在选择算子执行之前根据个体之间的支配关系进行了分层。其选择算子、交叉算子和变异算子与带精英选择的遗传算法没有区别。
非支配排序过程如下：
首先求出种群个体的Pareto解集，标记Pareto解集个体前沿编号为1。然后依次求剩余个体的Pareto解集，分别标记个体前沿编号为2、3、…i…直到种群个体全部分层。

下图是一个二维Pareto前沿面，对种群个体进行分层之后，rank1是前沿编号为1的个体，rank2是前沿编号为2的个体，rank3是前沿编号为3的个体，

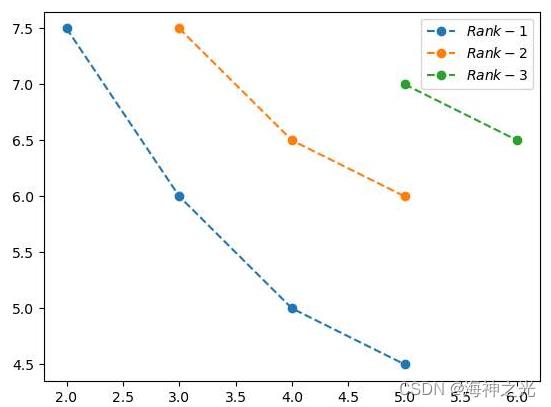
选出下一代个体：
同层个体按照拥挤度由小到大的顺序放入新的种群N 中，首先将种群中前沿面为1所有个体全部放入新的种群N中，若N 没满，继续放入前沿面为2，3…i…中的个体，直到种群N 满为止。

画出Pareto解集前沿图：
在三维坐标系中用坐标轴来表示充电时间、充电费用和充电桩利用率偏差，用颜色表示电网平均负载。画出4个优化目标的Pareto前沿图。

二、部分源代码

function Copy_of_NSGAII()
clc;format compact;tic;hold on
global fitvalue;
global fitvalue2;
global fitvalue3;
global fitvalue4;
global newpop;
global pop;   
global newpop_mut;   
global Best_individual;
   %---初始化/参数设定clear all
 
    generations=100;                                %迭代次数
    popnum=100;                                    %种群大小(须为偶数)
    M=8;                                            %个体长度
    N=5;
    cross_rate=0.95;
    mutate_rate=0.03;
    
  %  minvalue=repmat(zeros(1,poplength),popnum,1);   %个体最小值
  %  maxvalue=repmat(ones(1,poplength),popnum,1);    %个体最大值    
    initpop(popnum,M,N);                           % 初始化,产生新的初始种群
    
%---开始迭代进化
 
    for gene=1:generations  %开始 迭代 
        
%-------交叉 
          crossover(popnum,M,N, cross_rate);% 交叉操作
       % newpopulation=zeros(popnum,poplength);  %子代种群
       % for i=1:popnum/2                        %交叉产生子代
       %     k=randperm(popnum);                 %从种群中随机选出两个父母,不采用二进制联赛方法
       %      beta=(-1).^round(rand(1,poplength)).*abs(randn(1,poplength))*1.481; %采用正态分布交叉产生两个子代
       %     newpopulation(i*2-1,:)=(population(k(1),:)+population(k(2),:))/2+beta.*(population(k(1),:)-population(k(2),:))./2;    %产生第一个子代           
       %     newpopulation(i*2,:)=(population(k(1),:)+population(k(2),:))/2-beta.*(population(k(1),:)-population(k(2),:))./2;      %产生第二个子代
       %  end
%-------变异        
          mutation(popnum,M,N, mutate_rate);% 变异操作
       % k=rand(size(newpopulation));    %随机选定要变异的基因位
       % miu=rand(size(newpopulation));  %采用多项式变异
       % temp=k<1/poplength & miu<0.5;   %要变异的基因位
       % newpopulation(temp)=newpopulation(temp)+(maxvalue(temp)-minvalue(temp)).*((2.*miu(temp)+(1-2.*miu(temp)).*(1-(newpopulation(temp)-minvalue(temp))./(maxvalue(temp)-minvalue(temp))).^21).^(1/21)-1);        %变异情况一
       % newpopulation(temp)=newpopulation(temp)+(maxvalue(temp)-minvalue(temp)).*(1-(2.*(1-miu(temp))+2.*(miu(temp)-0.5).*(1-(maxvalue(temp)-newpopulation(temp))./(maxvalue(temp)-minvalue(temp))).^21).^(1/21));  %变异情况二
        
%-------越界处理/种群合并  

       newpop=[pop newpop_mut];
       % newpopulation(newpopulation>maxvalue)=maxvalue(newpopulation>maxvalue); %子代越上界处理
       % newpopulation(newpopulation<minvalue)=minvalue(newpopulation<minvalue); %子代越下界处理
       % newpopulation=[population;newpopulation];                               %合并父子种群
        
%-------计算目标函数值    
        index_1(newpop,M,N);%对个体的行驶时间和充电时间排序
        wait(newpop,M,N);
        fitness(newpop, M,N);
        fitness2(newpop, M,N);
        fitness3(newpop, M,N);
        fitness4(newpop, M,N);
        functionvalue=zeros(size(newpop,2),4);           %合并后种群的各目标函数值,这里的问题是ZDT1
        functionvalue(:,1)=fitvalue(1:size(newpop,2));
        functionvalue(:,2)=fitvalue2(1:size(newpop,2));
        functionvalue(:,3)=fitvalue3(1:size(newpop,2));
        functionvalue(:,4)=fitvalue4(1:size(newpop,2));
 
       % functionvalue=zeros(size(newpopulation,1),2);           %合并后种群的各目标函数值,这里的问题是ZDT1
       % functionvalue(:,1)=newpopulation(:,1);                  %计算第一维目标函数值
       % g=1+9*sum(newpopulation(:,2:poplength),2)./(poplength-1);
       % functionvalue(:,2)=g.*(1-(newpopulation(:,1)./g).^0.5); %计算第二维目标函数值
        
%-------非支配排序        
 
        fnum=0;                                             %当前分配的前沿面编号
        cz=false(1,size(functionvalue,1));                  %记录个体是否已被分配编号
        frontvalue=zeros(size(cz));                         %每个个体的前沿面编号
        [functionvalue_sorted,newsite]=sortrows(functionvalue);    %对种群按第一维目标值大小进行排序
        while ~all(cz)                                      %开始迭代判断每个个体的前沿面,采用改进的deductive sort
            fnum=fnum+1;
            d=cz;
            for i=1:size(functionvalue,1)
                if ~d(i)
                    for j=i+1:size(functionvalue,1)
                        if ~d(j)
                            k=1;                            
                            for m=2:size(functionvalue,2)
                                if functionvalue_sorted(i,m)>functionvalue_sorted(j,m)
                                    k=0;
                                    break
                                end
                            end
                            if k
                                d(j)=true;
                            end
                        end
                    end
                    frontvalue(newsite(i))=fnum;
                    cz(i)=true;
                end
            end
        end

三、运行结果

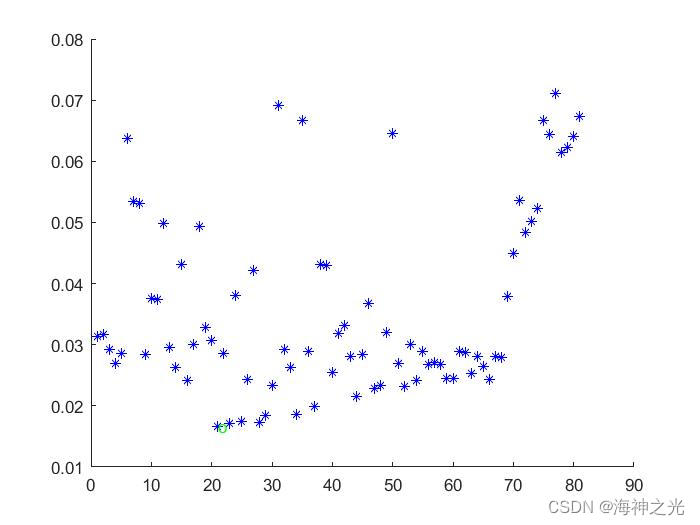
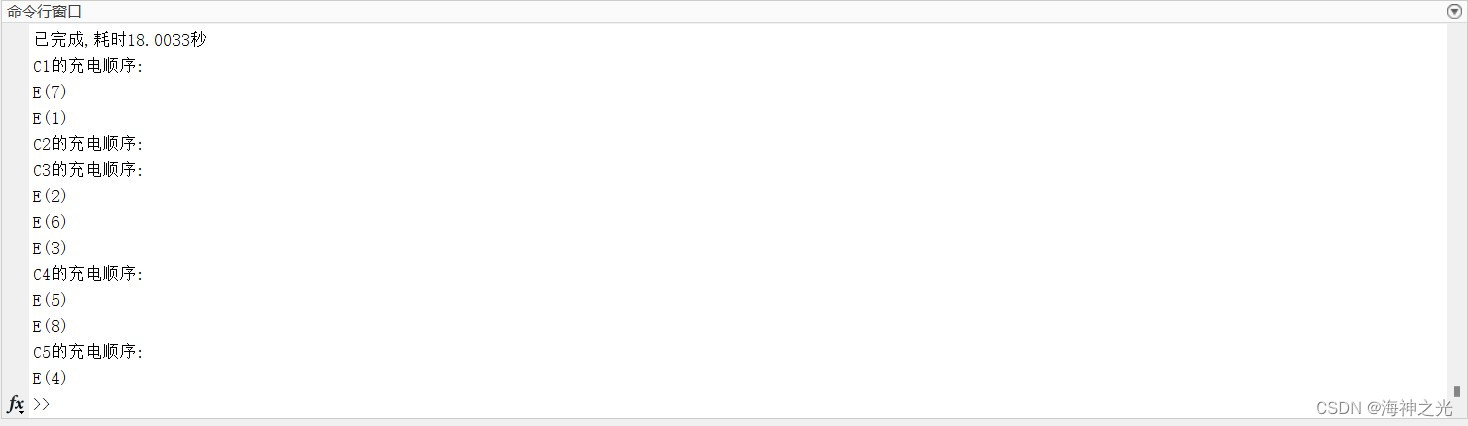
四、matlab版本及参考文献

1 matlab版本
2014a

2 参考文献
[1]李翠玉,胡雅梦,康亚伟,张德良.应用自适应遗传算法的电动汽车充放电协同调度[J].吉林大学学报(工学版)

3 备注
简介此部分摘自互联网，仅供参考，若侵权，联系删除