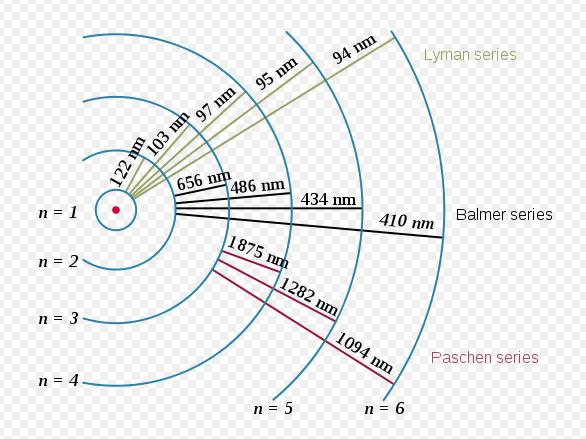
粒子受到激发而进入的激发态，不是粒子的稳定状态，如存在着可以接纳粒子的较低能级，即使没有外界作用，粒子也有一定的概率，自发地从高能级激发态（E2）向低能级基态（E1）跃迁，同时辐射出能量为（E2-E1）的光子，光子频率 ν=（E2-E1）/h。这种辐射过程称为自发辐射。众多原子以自发辐射发出的光，不具有相位、偏振态、传播方向上的一致，是物理上所说的非相干光。

1.3 受激辐射、激光

1917年，爱因斯坦从理论上指出：除自发辐射外，处于高能级E2上的粒子还可以另一方式跃迁到较低能级。他指出当频率为 ν=（E2-E1）/h的光子入射时，也会引发粒子以一定的概率，迅速地从能级E2跃迁到能级E1，同时辐射两个与外来光子频率、相位、偏振态以及传播方向都相同的光子，这个过程称为受激辐射。

可以设想，如果大量原子处在高能级E2上，当有一个频率 ν=（E2-E1）/h的光子入射，从而激励E2上的原子产生受激辐射，得到两个特征完全相同的光子，这两个光子再激励E2能级上原子，又使其产生受激辐射，可得到四个特征相同的光子，这意味着原来的光信号被放大了。这种在受激辐射过程中产生并被放大的光就是激光。

1.4 激光的难点

爱因斯坦1917提出受激辐射，激光器却在1960年问世，相隔43年，为什么？

主要原因是，普通光源中粒子产生受激辐射的概率极小。

当频率一定的光射入工作物质时，受激辐射和受激吸收两过程同时存在，受激辐射使光子数增加，受激吸收却使光子数减小。物质处于热平衡态时，粒子在各能级上的分布，遵循平衡态下粒子的统计分布律。按统计分布规律，处在较低能级E1的粒子数必大于处在较高能级E2的粒子数。这样光穿过工作物质时，光的能量只会减弱不会加强。要想使受激辐射占优势，必须使处在高能级E2的粒子数大于处在低能级E1的粒子数。这种分布正好与平衡态时的粒子分布相反，称为粒子数反转分布，简称粒子数反转。

如何从技术上实现粒子数反转是产生激光的必要条件。

1.5 粒子数反转

理论研究表明，任何工作物质，在适当的激励条件下，可在粒子体系的特定高低能级间实现粒子数反转。若原子或分子等微观粒子具有高能级E2和低能级E1，E2和E1能级上的布居数密度为N2和N1，在两能级间存在着自发发射跃迁、受激发射跃迁和受激吸收跃迁等三种过程。受激发射跃迁所产生的受激发射光，与入射光具有相同的频率、相位、传播方向和偏振方向。因此，大量粒子在同一相干辐射场激发下产生的受激发射光是相干的。受激发射跃迁几率和受激吸收跃迁几率均正比于入射辐射场的单色能量密度。当两个能级的统计权重相等时，两种过程的几率相等。在热平衡情况下N2<N1，所以受激吸收跃迁占优势，光通过物质时通常因受激吸收而衰减。外界能量的激励可以破坏热平衡而使N2>N1，这种状态称为粒子数反转状态。在这种情况下，受激发射跃迁占优势。光通过一段长为l的处于粒子数反转状态的激光工作物质（激活物质）后，光强增大eGl倍。G为正比于（N2-N1）的系数，称为增益系数，其大小还与激光工作物质的性质和光波频率有关。一段激活物质就是一个激光放大器。如果，把一段激活物质放在两个互相平行的反射镜（其中至少有一个是部分透射的）构成的光学谐振腔中（图1），处于高能级的粒子会产生各种方向的自发发射。其中，非轴向传播的光波很快逸出谐振腔外：轴向传播的光波却能在腔内往返传播，当它在激光物质中传播时，光强不断增长。如果谐振腔内单程小信号增益G0l大于单程损耗δ（G0l是小信号增益系数），则可产生自激振荡。

原子的运动状态可以分为不同的能级，当原子从高能级向低能级跃迁时，会释放出相应能量的光子（所谓自发辐射）。

1.6 激光器的发展

激光器——能发射激光的装置。

1954年制成了第一台微波量子放大器，获得了高度相干的微波束。

1958年A.L.肖洛和C.H.汤斯把微波量子放大器原理推广应用到光频范围，

1960年T.H.梅曼等人制成了第一台红宝石激光器。

1961年A.贾文等人制成了氦氖激光器。

1962年R.N.霍耳等人创制了砷化镓半导体激光器。

1.7 激光的频率与能量

光的颜色由光的波长（或频率）决定。一定的波长对应一定的颜色。

太阳辐射出的可见光段的波长分布范围约在0.76微米至0.4微米之间，对应的颜色从红色到紫色共7种颜色，所以太阳光谈不上单色性。发射单种颜色光的光源称为单色光源，它发射的光波波长单一。比如氪灯、氦灯、氖灯、氢灯等都是单色光源，只发射某一种颜色的光。单色光源的光波波长虽然单一，但仍有一定的分布范围。如氖灯只发射红光，单色性很好，被誉为单色性之冠，波长分布的范围仍有0.00001纳米，因此氖灯发出的红光，若仔细辨认仍包含数十种红色。由此可见，光辐射的波长分布区间越窄，单色性越好。 [1]

激光器输出的光，波长分布范围非常窄，因此颜色极纯。以输出红光的氦氖激光器为例，其光的波长分布范围可以窄到2×10^(-9)米级别，是氪灯发射的红光波长分布范围的万分之二。由此可见，激光器的单色性远远超过任何一种单色光源。

光子的能量是用E=hv来计算的，其中h为普朗克常量，v为频率。由此可知，频率越高，能量越高。激光频率范围3.846×10^（14）Hz到7.895×10^（14）Hz。

1.8 电磁波谱

（1）无线电波——波长从几千米到0.3米左右，一般的电视和无线电广播的波段就是用这种波；

（2）微波——波长从0.3米到10^-3米，这些波多用在雷达或其它通讯系统；

（3）红外线——波长从10^-3米到7.8×10^-7米；

（4）可见光——这是人们所能感光的极狭窄的一个波段。波长从780—380nm。

光是原子或分子内的电子运动状态改变时所发出的电磁波。

由于它是我们能够直接感受而察觉的电磁波极少的那一部分；

（5）紫外线——波长从3 ×10^-7米到6×10^-10米。这些波产生的原因和光波类似，常常在放电时发出。由于它的能量和一般化学反应所牵涉的能量大小相当，因此紫外光的化学效应最强；

（6）伦琴射线(X射线)—— 这部分电磁波谱，波长从2×10^-9米到6×10^-12米。伦琴射线（X射线）是电原子的内层电子由一个能态跳至另一个能态时或电子在原子核电场内减速时所发出的；

（7）伽马射线——是波长小于0.1纳米的电磁波。这种不可见的电磁波是从原子核内发出来的，放射性物质或原子核反应中常有这种辐射伴随着发出。γ射线的穿透力很强，对生物的破坏力很大。由此看来，激光能量并不算很大，但是它的能量密度很大（因为它的作用范围很小，一般只有一个点），短时间里聚集起大量的能量，用做武器也就可以理解了。