浪潮“源”AI大模型如何求解数学应用题

Posted 2022-07-13 CSDN云计算

编辑 | 宋慧

供稿 | 浪潮

“源1.0”大模型是浪潮信息发布的中文巨量模型，参数量高达2457亿，在中文语言能力理解和生成评测基准CUGE总榜中取得榜首，并获得语言理解（篇章级）、语言生成、对话交互、多语言、数学推理等5项评测最佳成绩。其中在数学推理评测中，源1.0大模型完成1000道小学数学应用题，以76.9的高分大幅领先。

数学对逻辑和推理能力有极强的要求，以往大模型在数学领域表现欠佳。源1.0为何能取得这么好的成绩？本文将介绍数学推理任务的背景、研究现状，以及源1.0在数学推理任务方面的解决方案和表现。

一、数学单词问题的研究背景及意义

数学单词问题，即Math Word Problem（MWP），其主要目标是根据自然语言文字描述的内容解决相应的数学问题。也就是说，对于给定的数学问题，模型需要理解相关文字的数学含义，并推理出正确的表达式。

一个典型的MWP示例如下。

问题：“快车和慢车同时从相距450千米的两城相对开出，4.5小时后两车还相距90千米，快车和慢车的速度比为9：7，慢车每小时行多少千米？”
表达式：(450-90)/4.5*7/(9+7)
结果：35

不难发现，该题目除了要求模型能够理解基本的加减乘除法之外，还需要理解什么是比例问题。此外，若将问题中的“相对开出”改为“相反方向开出”，将会导致问题的数学逻辑大相径庭。如何让模型分辨出语言表达上的差异，并正确地推理出对应的表达式是MWP任务的基本要求。

需要注意的是，在上面的MWP中，表达式中所需的数字量均可以在问题中找到，但在某些情况下，表达式中所需要的数字量并不会全部包含在问题中。例如，在含有分数的MWP示例中（如下红框中所示），需要根据题目中的数学逻辑，在表达式中额外添加相应的数字量“1”。同样的问题还常见于计算圆的周长或面积时，需要额外添加数字量“3.14”。

问题：“一根电线长80米，第一次截去的全长的2/5，第二次截去了余下的1/4，这根电线还剩多少米？”
表达式：80*(1-2/5-(1-2/5)*1/4)
结果：36

毫无疑问，MWP任务给模型的语言理解能力和数学推理能力都带来了极大的挑战，如何解决MWP任务也是NLP领域的研究热点之一。

二、数字单词问题的研究现状

实际上，直到2016年MWP的任务精度仍然比较有限。关于MWP任务在2016年之前的研究在此不作细述，相关综述可参考论文：How well do Computers Solve Math Word Problems? Large-Scale Dataset Construction and Evaluation (Huang et al., ACL 2016)

近几年，借助DNN解决MWP任务的方法显著提升了MWP任务精度，这些方法大致可以分为以下三类：基于seq2seq模型、基于seq2tree模型和基于预训练模型。

1、基于seq2seq模型

该方法是由Wang Yan等学者[1]首次应用在MWP任务上，并在大规模多题型的数据集（Math23K）上取得了显著的效果（对于Math23K数据集将在后续内容中进行说明）。该方法本质上是采用Encoder-Decoder（enc-dec）结构直接完成了从“问题”到“表达式”的映射。值得一提的是，前述的Math23K数据集规模较大题型较多（约22000道），是目前MWP任务评测的benchmark。

此外，通过设计不同的Encoder和Decoder结构可以得到改进后的seq2seq方法。不过令人惊讶的是，Transformer结构的enc-dec并未在Math23K数据集上表现出明显的优势；而采用LSTM结构作为enc-dec的LSTMVAE方法表现最佳。

2、基于seq2tree模型

基于Seq2tree模型实际上是基于seq2seq模型的变种，简单来说，就是将number-mapping后的表达式转化为树结构作为模型训练的输出（如图1所示），由于父节点与子节点处的数学符号以及连接方式是固定的，这种方式能够有效地限制表达式的多样性。这里，表达式的多样性可以理解为针对同一个问题可以列出不同的表达式，例如n1+n2-n3还可以写成n2+n1-n3或者n1+(n2-n3)。

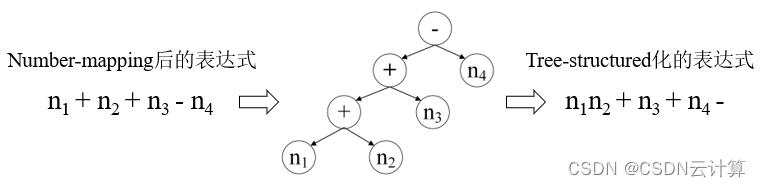
图1 树结构化的表达式生成示意[2]

在前述基础下，基于seq2tree模型的MWP任务解决方法应运而生，其核心思想是将原先的decoder被替换成了tree-based decoder。至此，MWP任务解决思路似乎主要集中在如何替换encoder和decoder问题上。例如，Wang Lei等学者又调整了encoder结构，提出了Graph2tree的方法并且在Math23K任务上精度高达75%。

3、基于预训练模型

Wang Lei等学者[3]发现BERTGen和RoBERTGen（Dec：BERT、RoBERT；Enc：Transformer）在Math23K数据集上表现较为优秀（76.9%）。此外，他们还验证了GPT-2模型在Math23K数据集上的表现（74.3%），结果稍逊于基于BERT模型的方法，这可能是GPT-2模型结构的原因（Decoder结构）。

4、其他MWP任务解决方法

根据前述方法，可以看到的是encoder采用BERT模型较好，decoder采用tree-based方式较好，若将两者结合形成BERT encoder + tree-based decoder[4]，其在Math23K数据集上的精度达到了惊人的84.4%，是目前Math23K任务的baseline。

此外，在众多MWP任务解决方法中Recall and learn方法[5]是十分值得一提的。该方法跳出了经典的enc-dec结构，通过模拟人脑在解决问题时的类比能力，推理出数学问题的表达式，最终该方法在Math23K任务上的精度能够达到82.3%。

三、“源1.0”大模型的MWP任务解决方案

需要指出的是，尽管构建单个技能模型在一定程度上能够较好地完成MWP任务，但现有技能模型绝大多数仍采用的是encoder-decoder结构，针对类似decoder结构下（如GPT-2）的模型数值推理能力的研究仍然较少。此外，从实现通用人工智能的目标来看，提升通用大模型的数值推理能力是十分必要的。

接下来，笔者将详细介绍浪潮信息的“源1.0”大模型（decoder结构）在Math23K任务上的相关工作，希望能够对提升通用大模型的数值推理能力有所启发。“源1.0”大模型在数学推理能力方面目前位列中文语言能力评测基准CUGE榜首。

​​​​​​​1、目标导向的问答式Prompt设计

Math23K的标准数据样例为：

　"text": "某班学生参加数学兴趣小组，其中，参加的男生是全班人数的20%，参加的女生是全班人数的(2/7)多2人，不参加的人数比全班人数的(3/5)少5人，全班有多少人？",

　"segmented_text": "某班 学生 参加 数学 兴趣小组 ， 其中 ， 参加 的 男生 是 全班 人数 的 20% ， 参加 的 女生 是 全班 人数 的 (2/7) 多 2 人 ， 不 参加 的 人数 比 全班 人数 的 (3/5) 少 5 人 ， 全班 有 多少 人 ？",

　"equation": "x=(5-2)/(20%+(2/7)+(3/5)-1)",

　"label": "35"

其中“text”和“equation”分别对应了任务的问题和表达式信息。在尝试过各种prompt后，最终确定的prompt设计如下。这种prompt设计将原本的问题拆分成了题干和待求解问题（“问：全班有多少人”）两个部分，这是由于“问：”后面的内容对表达式的生成十分关键。例如，“全班有多少人”和“全班女生有多少人”所对应的表达式是完全不同的。

某班学生参加数学兴趣小组，其中，参加的男生是全班人数的20%，参加的女生是全班人数的(2/7)多2人，不参加的人数比全班人数的(3/5)少5人，问：全班有多少人？答: x=(5-2)/(20%+(2/7)+(3/5)-1)

​​​​​​​2、相似启发式数据增强方法

Math23K数据集的题型虽然较为丰富，但题型分布并不均匀。例如，涉及图形周长、面积和体积类的问题显然比其他题目类型要少，为保证模型在各类数学题型上均有较好的表现，有必要将该类型的题目扩充。

本文采用了Ape210K数据集[6]对Math23K训练集进行扩充，Ape210K数据集是另一种较为常用的中文应用数学题集，其题型更为丰富且题量更大（训练集约20万道题）。然而，为保证模型在Math23K测试集上有良好的表现，并不能简单地将Math23K和Ape210K数据集混合在一起。为保证数据增强的有效性，本文提出了一种相似启发式数据增强方法（如图2所示）。

该方法针对Math23K训练集中的每一道题，首先判断是否属于图形周长、面积和体积类题目。若属于，则top-K取值为2，同时通过相似题检索从Ape210K中召回对应的相似题；若不属于，则top-K取值为1，同样进行相似题检索。最后，将找到的相似题添加至Math23K训练集中，数据增强后的训练集约包含42000道题。

图2 相似启发式数据增强方法

​​​​​​​3、Reset-position-id与reset-attention-mask设计

输入到模型的一个batch中通常包含多道应用题，且会出现截断等问题。为避免不同题目和表达式之间相互影响，对模型进行reset-position-id和reset-attention-mask处理。图3示意了reset前后的对比，采用了[eod]对不同题目之间做切割，在reset-pos-id之前，其位置编码按照从左到右的顺序排列；reset-pos-id之后，位置编码按照单个题目进行顺序排列。类似的，在reset-attn-mask之前，掩码矩阵对应的是batch尺寸的下三角矩阵；reset-attn-mask后，原先的掩码矩阵被拆分成若干小的掩码矩阵，每个小掩码矩阵对应单个题目尺寸的下三角矩阵。

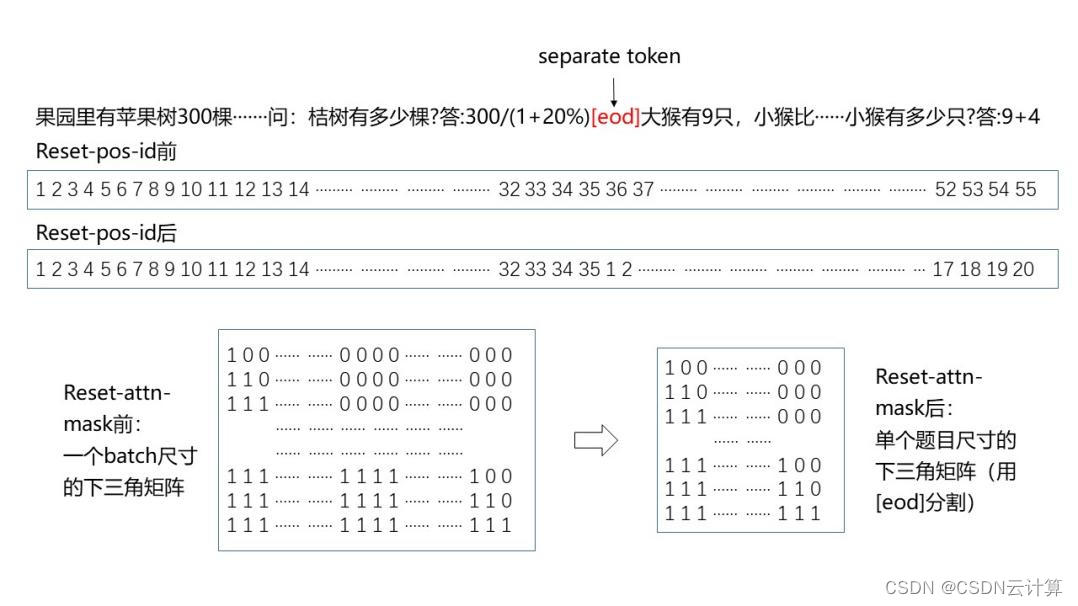
图3 reset-pos-id和reset-attn-mask前后对比（示意）

四、训练参数及结果

训练过程的主要参数设置如下。

表1 模型训练部分参数

参数	数值
Seq-length	2048
Batch-size	256
Learning-rate	5e-6
Train-iters	400

在训练了400个iteration后，模型的loss收敛至0.39（图4）。

图4 模型loss曲线

之后，在Math23K测试集上对所提方法的精度进行了测试，并与现有相关方法的结果进行对比（表2）。不难看出，与BERT、GPT-2以及CPM-2模型相比，所提方法下的“源1.0”大模型在Math23K任务上的精度最高。

表2 源1.0模型与BERT、GPT等在Math23K测试集上的对比（相关结果见参考文献[4]）

模型名称	Encoder-Decoder	Math23K精度（%）
BERTGen	是	76.6
RoBERTGen	是	76.9
CPM-2	是	69.4
GPT-2	Decoder结构	74.3
源1.0	Decoder结构	76.9

五、总结与展望

为提升decoder结构下的通用大模型在MWP任务上的精度，本文提出了一种目标导向的问答式prompt设计方法，该方法有利于引导模型建立问题与表达式之间的准确对应关系；同时提出了一种相似启发式数据增强方法，通过相似句召回的方式对数据集进行扩充，克服了原有数据集中题型分布不均匀的问题；此外，采用了重置位置编码和掩码矩阵的方法，解决了单个batch中的题目之间相互影响的问题。最后，在Math23K数据集上验证了所提方法，结果证明了“源1.0”模型有很强的数学推理能力。

针对MWP任务，“源1.0”模型后续将开展的工作包括：

1. 合理利用Number-mapping和tree结构的数据前处理，以及类似于recall and learn方法中的掩码矩阵设计，进一步提高“源1.0”在MWP任务上生成答案精度。
2. 虽然“源1.0”仅在Math23K任务上取得了较好的成绩，且目前还不能解决全部的MWP题型，但已经证明了“源1.0”模型具备了较强的数学推理能力。如何进一步挖掘“源1.0”在MWP任务上的潜力，以解决更为复杂的多元方程以及几何题型的问题，是我们后续准备继续深入研究的重要方向。

参考文献

[1] Yan Wang, Xiaojiang Liu, Shuming Shi (2017). Deep Neural Solver for Math Word Problems.

[2] Lei Wang, Yan Wang, Deng Cai, et al (2018). Translating a Math Word Problem to an Expression Tree.

[3] Yihuai Lan, Lei Wang, Qiyuan Zhang, et al (2021). MWPToolkit: An Open-Source Framework for Deep Learning-Based Math Word Problem Solvers

[4] Zhenwen Liang, Jipeng Zhang, Lei Wang, et al (2021). MWP-BERT: Numeracy-Augmented Pre-training for Math Word Problem Solving

[5] Shifeng Huang, Jiawei Wang, Jiao Xu, Da Cao, and Ming Yang. (2021). Recall and Learn: A Memory-augmented Solver for Math Word Problems.

[6] Wei Zhao, Mingyue Shang, Yang Liu, et al (2020). Ape210K: A Large-Scale and Template-Rich Dataset of Math Word Problems.