第一节3：DBSCAN性能分析优缺点和参数选择方法

Posted 2022-07-09 快乐江湖

文章目录

• 七：性能分析
• 八：优缺点
• • （1）优点
  • （2）缺点
• 九：参数选择
• • （1）修改参数的基本原则
  • （2）根据`K-dist`图调参
• 十：DBSCAN算法和K-Means算法比较

七：性能分析

DBSCAN算法对数据集中的每个点都要检索其邻域内的所有点，时间复杂度为$O(n^2)$。但在低纬空间中，若采用$k$-$d$树、$R$树等结构，可以有效地检索特定点给定距离内的所有点，其时间复杂度可以降低到$O(nlogn)$

八：优缺点

（1）优点

①：可以对任意形状的稠密数据集进行聚类

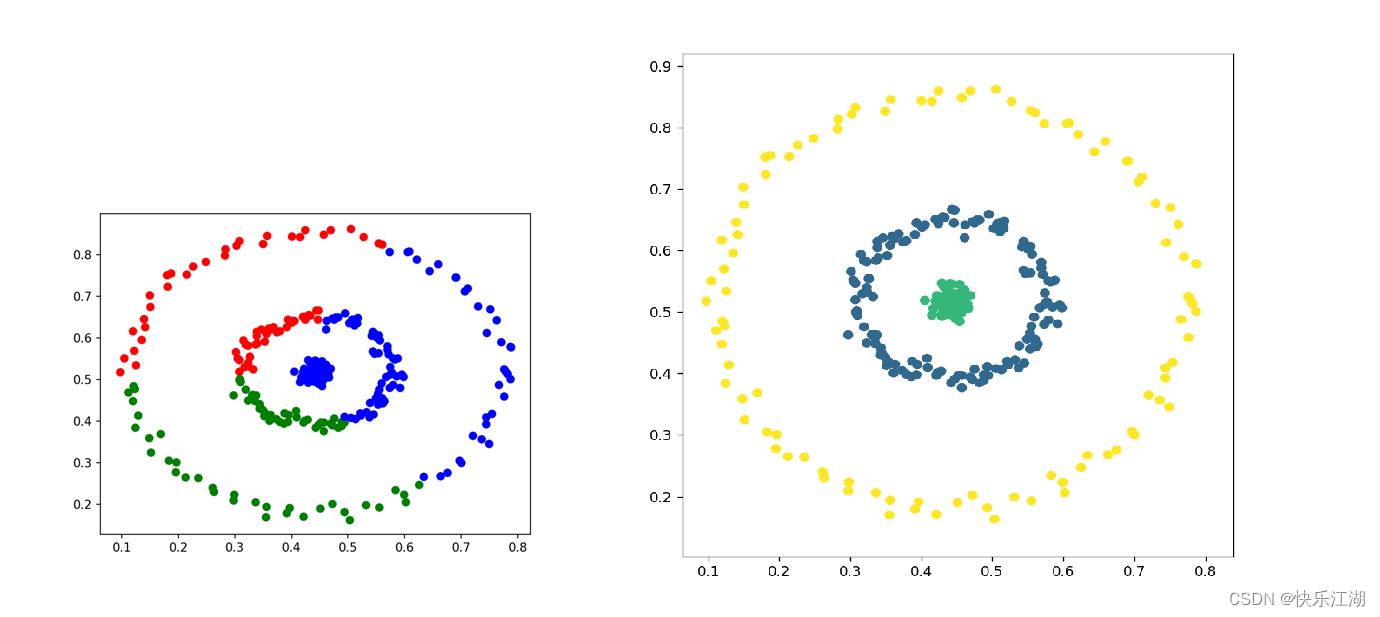
②：可以在聚类的同时发现异常点，对数据集中的异常点不敏感

③：不需要指定簇数，并且多次实验结果往往是相同的

（2）缺点

①：如果样本集的密度不均匀、聚类间距差相差很大时，聚类质量较差，这时用DBSCAN聚类一般不适合

②：调参相较于K-Means复杂一点，不同参数组合对聚类效果有很大影响

③：由于传统的欧式距离不能很好处理高纬数据，所以对于距离定义较难给出好的解决方案

④：DBSCAN算法适合处理不同簇的密度相对比较均匀的情况，当不同簇的密度变化很大时会出现一些问题

• 从上一节所展示的聚类效果图中，大家可能会发现该算法很容易把一些数据点标记为噪声
  

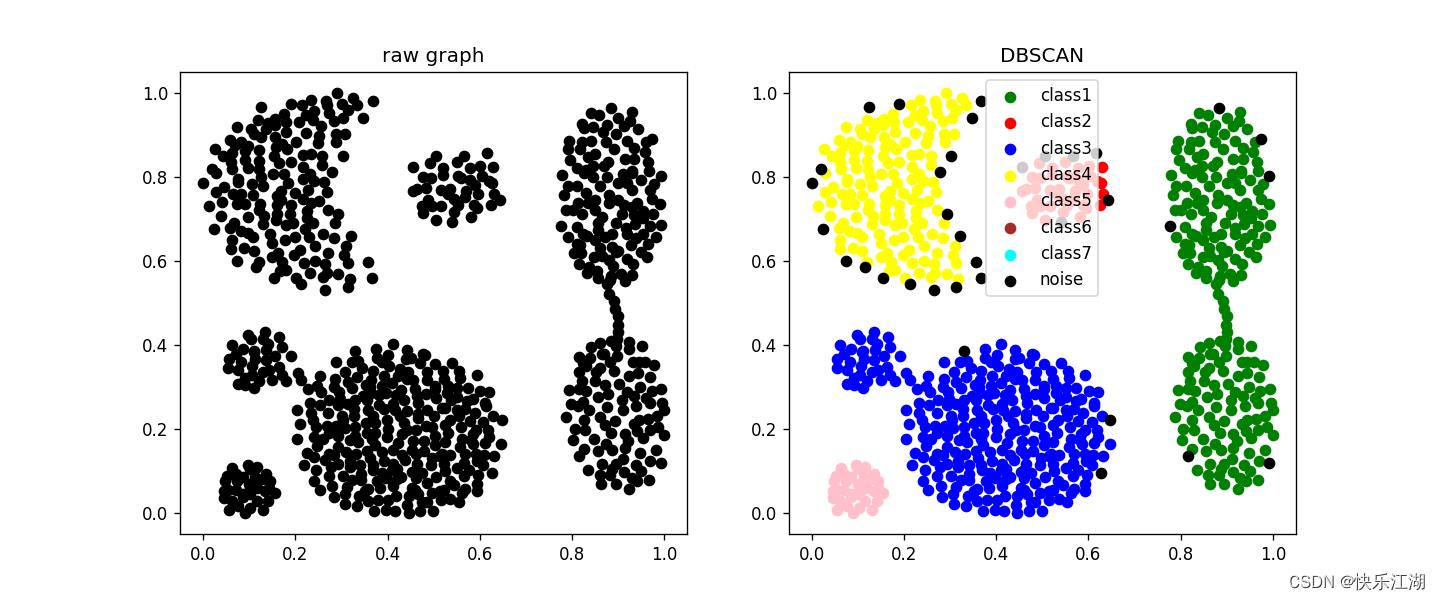
九：参数选择

（1）修改参数的基本原则

当可视化完成后，我们可以根据其聚类的结果来微调参数

• min_pts：一般选择维度+1或者维度×2即可
• eps：如果所分的类少了，那就把eps调小一点；如果所分的类多了，那就把eps调大一点

（2）根据K-dist图调参

调参方法：可以用观察第$k$个最近邻距离（$k$距离）的方法来确定参数。对于簇中的某个点，如果$k$不大于簇的样本个数，则$k$距离将会很小，然后对于噪声，$k$距离将会很大。因此：对于任意一个正整数$k$，计算所有数据点的$k$距离，然后以递增方式排序，然后绘制$k$-距离图，在拐点位置对应的就是合适的eps， 因为在拐点位置往往遇到了边界点或者噪声点

• $k$距离：对于给定的数据集$P$=$p_1,p_2,...,p_n$，计算点$p(i)$到数据集$D$的子集$S$中所有点之间的距离，距离按从小到大的顺序排序，则$d(k)$就称之为$k$距离

具体步骤如下

1. 确定K值，一般取2*维度-1
2. 绘制K-dist图
3. 拐点位置（波动最大的地方）为eps（可以取多个拐点尝试）
4. min_pts可以取K+1

k = 3  # 取2*2-1
k_dist = select_minpts(train_data, k)  # K距离图
k_dist.sort()  # 排序（默认升序）
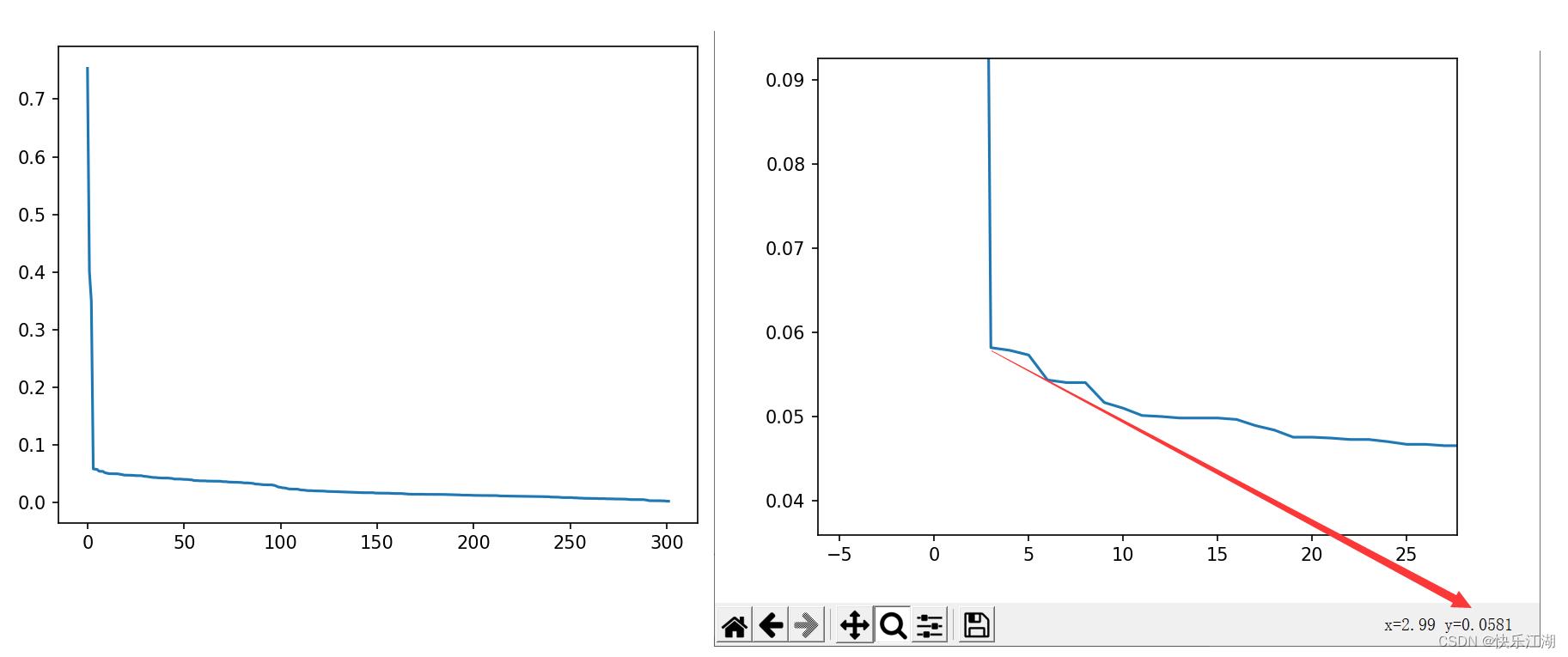
plt.plot(np.arange(k_dist.shape[0]), k_dist[::-1])  # 绘图时从大到小
plt.show()


def select_minpts(data_set, k):
    k_dist = []
    for i in range(data_set.shape[0]):
        dist =  (((data_set[i] - data_set)**2).sum(axis=1)**0.5)
        dist.sort()
        k_dist.append(dist[k])
    return np.array(k_dist)

如下eps建议取0.0581

十：DBSCAN算法和K-Means算法比较

	DBSCAN	K-Means
算法思想	基于密度	基于划分
所需参数	Eps和MinPts	簇个数$k$
数据要求	对数据分布不做任何假设	假设所有簇来自球形的高斯分布
高维数据	不适合	适合（稀疏的）
形式化	不能	能够形式化为最小化每个点到质心的误差平方和的优化问题
稳定性	稳定	不稳定
时间复杂度	$O(n^2)$	$O(n)$