码蹄集 - MT3435 · 赋值 - 二分图问题 - 图文讲解

Posted 2022-07-02 Tisfy

传送门

• • 赋值
  • • 题目描述
    • 输入描述
    • 输出描述
    • 样例一
    • • 输入
      • 输出
• 题目分析
• • 二分图简述
  • 划分为二分图
  • 结果计算
• AC代码

---

赋值

• 赋值 .

时间限制：1秒
空间限制：256M

---

题目描述

给定一张含有n个结点m条边的无向图，你必须给每个点赋一个点权（必须是1 2 3中的一个），问有多少种不同的赋值方式（这不就是3^n吗？？？，往下看）

但有一个限制条件：那就是每条边的两个端点奇偶性必须不同

---

输入描述

第一行输入两个整数n，m

接下来的m行每行两个整数u，v代表u和v之间有一条边

（数据保证没有自环,没有重边，不保证是连通图）

（1<=n,m<=300000,1<=u,v<=n)

---

输出描述

输入总的方案数，答案可能非常大，结果对1e9+7取模

---

样例一

输入

4 4
1 2
2 3
3 4
1 4

输出

8

题目分析

二分图简述

这道题本质上就是二分图问题。

二分图也就是说要把一个图的所有节点划分到两个集合$A$、$B$中，使得每一条边两端的节点都不在一个集合中。

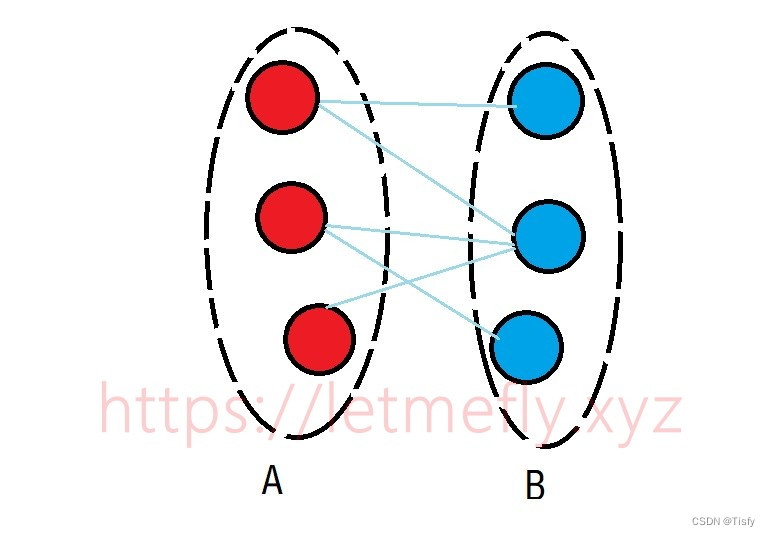
通俗地讲，所有红色的节点之间不能有边直接相连，所有蓝色的节点之间不能有边直接相连。

如果我们把一个连通图分成了上述集合$A$和$B$，那么我们就可以把$A$中节点全部赋值为奇数，$B$中节点全部赋值为偶数。

因为奇数有$1$和$3$两种，偶数只有$2$这一种，所以赋值方案数为$2^a$，其中$a$是$A$中的节点的个数。

同理，我们也可以把$A$中节点赋值为偶数，$B$中节点赋值为奇数，则又有$2^b$种赋值方案，其中$b$是集合$B$中的节点的个数。

综上所述，一个能把节点分成集合$A$和$B$的二分图，节点赋值为$1、2、3$且相邻节点奇偶性不同的赋值方案为$2^a+2^b$

那么问题就变成了如何把题目给定的图划分成不同的二分图。

划分为二分图

我们可以用$color[i]$表示节点$i$的分组情况。$0$代表为分组，$1$代表该节点被划分到了集合$A$中，$2$代表划分到了集合$B$中。

遍历每一个节点，如果这个节点还未被划分，那么就将这个节点作为一个新的二分图的“源点”，$BFS$一遍并统计这个子图的集合$A、B$中节点的个数。

注意：若$BFS$过程中发现了“一条边两端的节点属于同一个集合”的情况，则此图无法划分为二分图，赋值方案数为$0$。（如下图绿色边所示）

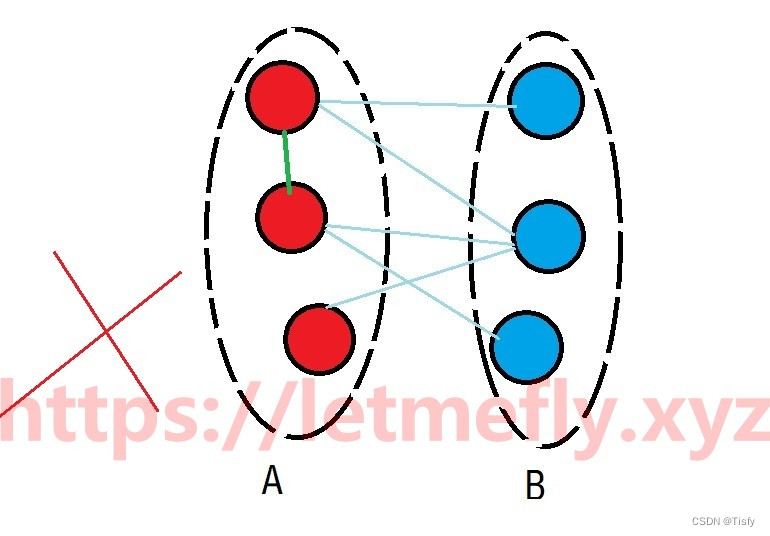
结果计算

当我们把这个图划分为不同的二分图后，每个二分图的方案数之积，就是总方案数。

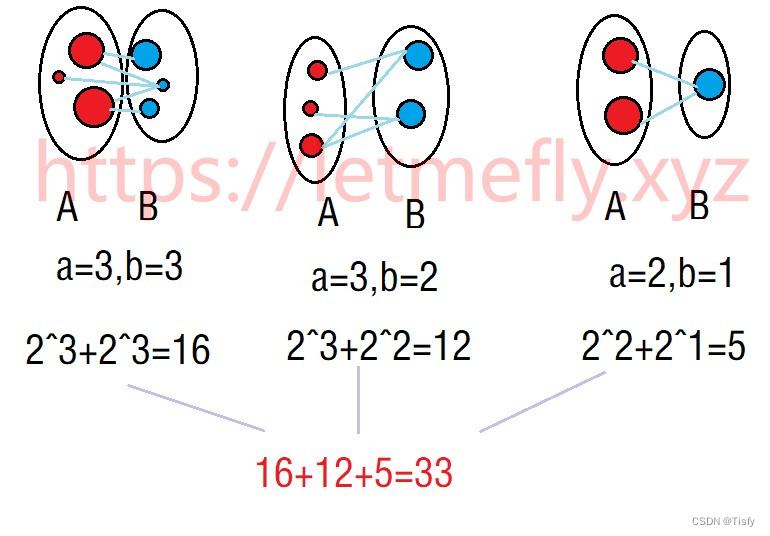
具体实现可参考代码注释

AC代码

// 给定一张含有n个结点m条边的无向图，每条边的两个端点奇偶性必须不同，有多少种不同的赋值方式
#include <bits/stdc++.h>
using namespace std;
#define mem(a) memset(a, 0, sizeof(a))
#define dbg(x) cout << #x << " = " << x << endl
#define fi(i, l, r) for (int i = l; i < r; i++)
#define cd(a) scanf("%d", &a)
typedef long long ll;

const ll mod = 1e9 + 7;
vector<int> a[300010];  // 存图
ll Pow[300010] = 1;  // Pow[i] = 2^i
int color[300010] = 0;  // 分组情况，默认值0表示未分组

int main() 
    int n, m;
    cin >> n >> m;
    for (int i = 1; i <= n; i++)   // 预处理，计算2^i
        Pow[i] = (Pow[i - 1] * 2) % mod;
    
    for (int i = 0; i < m; i++)   // 读入图
        int l, r;
        scanf("%d%d", &l, &r);
        a[l].push_back(r);
        a[r].push_back(l);
    
    ll ans = 1;  // 答案
    for (int i = 1; i <= n; i++)   // 遍历所有节点
        if (!color[i])   // 还没被染色（说明还没有被划分到某个子图中）
            int aNode = 0, bNode = 0;  // 二分图A、B中的节点个数
            queue<int> q;  // bfs队列
            function<void(int, int)> addOneNode = [&](int thisNode, int thisColor)   // 处理一个新的节点
                color[thisNode] = thisColor;  // 标注分组
                q.push(thisNode);  // 入队
                if (thisColor == 1)  // 统计集合中节点的个数
                    aNode++;
                else
                    bNode++;
            ;
            addOneNode(i, 1);  // 先处理这个子图的“源点”
            while (q.size())   // 开始BFS
                int thisNode = q.front();
                q.pop();  // 队首节点
                int toColor = (color[thisNode] == 1 ? 2 : 1);  // 它的相邻节点所属的集合
                for (int& toNode : a[thisNode])   // 遍历这个节点的所有边
                    if (!color[toNode])   // 相邻节点还未被分组
                        addOneNode(toNode, toColor);  // 处理这个相邻节点（划分集合、入队、统计）
                    
                    else   // 这个相邻节点已经被分组了
                        if (color[toNode] == color[thisNode])   // 并且和这个节点还被分到了一组中
                            puts("0");  // 无法划分为二分图，方案数为0
                            return 0;
                        
                    
                
            
            ans = (ans * (Pow[aNode] + Pow[bNode])) % mod;  // 各个子图的方案数之积
        
    
    cout << ans << endl;
    return 0;

每周提前更新菁英班周赛题解，点关注，不迷路

原创不易，转载请附上原文链接哦~
Tisfy：https://letmefly.blog.csdn.net/article/details/125537979