《Cross-view Transformers for real-time Map-view Semantic Segmentation》论文笔记

Posted 2022-07-01 m_buddy

参考代码：cross_view_transformers

1. 概述

介绍：这篇文章提出了一种新的2D维度的bev特征提取方案，其通过引入相机先验信息（相机内参和外参）构建了一个多视图交叉注意力机制，能够将多视图特征映射为BEV特征。对于构建其多视图特征于bev特征映射关系的桥梁，这便通过是BEV位置编码（需要加上原本的的bev queries作为refine，对于这里写的“编码”即是文中的embedding）和由根据相机标定结果（内参和外参）演算得到的相机位置编码（camera-aware embedding）、多视图特征做attention得到，这个步骤在文中叫做cross view attention。整体上文章的网络前端使用CNN作为特征抽取网络，中端使用CNN多级特征作为输入在多视图下优化BEV特征（也就是使用了级联优化），后端使用CNN形式的解码器进行输出。整体运行简洁高效，能够在2080Ti GPU上达到实时的效果。

这篇文章提出了基于transformer的bev特征提取网络（对于2D的bev），对于bev下的queries会通过加上map-view embedding进行refine得到最终queries。同样在多视图特征（由CNN网络得到）上也会添加camera-view的embedding进行refine得到key。同时为了感知道路的3D位置几何关系还对相机位置进行embedding（代码中为减去操作），并与上述的两种embedding进行关联。最后原多视图特征也会经过线型映射作为val，这样构建attention计算。上述提到的内容可参见下图作为辅助说明

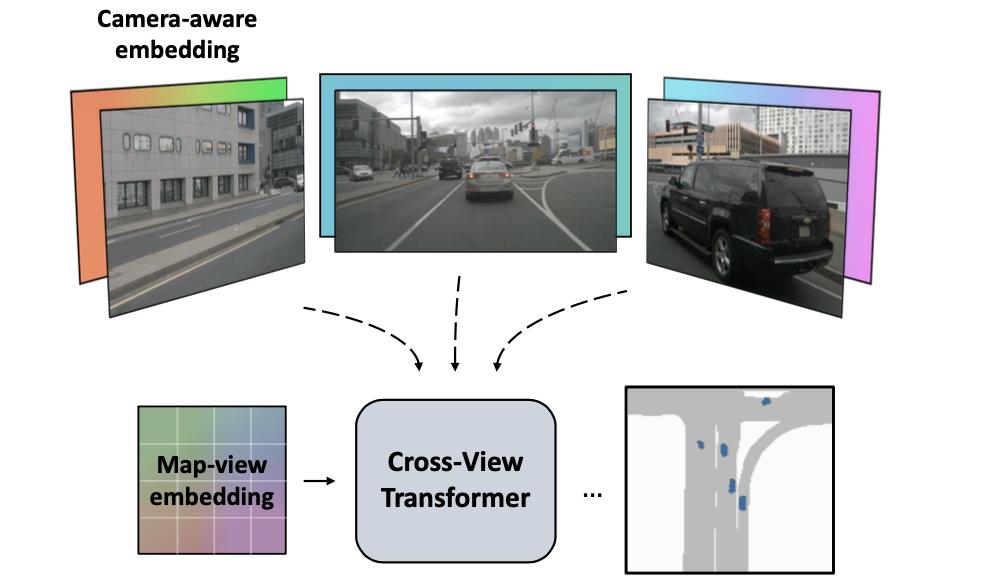
2. 方法设计

2.1 网络pipeline

文章提出的整体算法如下图所示：

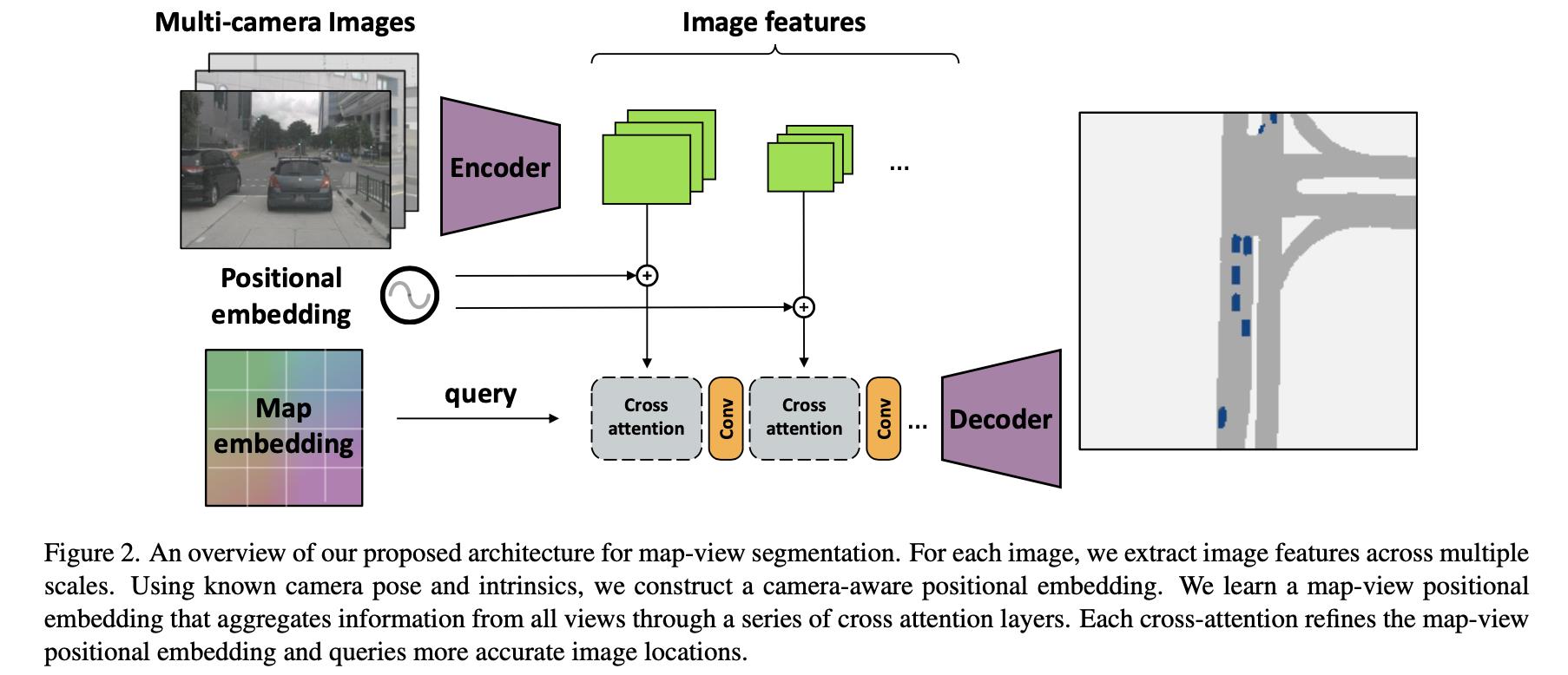
在上图中输入的数据为多视图数据$I_k\in R^{W\ast H\ast 3},R_k\in R^{3\ast 3},K_k\in R^{3\ast 3},t_k\in R^3{}_{k=1}^n$（分别代表图像、旋转矩阵、内参矩阵、平移向量）。其经过如下几步得到最后的结构：

• 1）CNN网络从多视图数据提取CNN特征${\delta }_k,k=1,\dots ,n$，这些特征会经过一个线型映射得到attention中的val。
• 2）CNN特征基础上添加camera-view embedding（也就是上图中的positional embedding，依赖于各自视图标定得到的内外参数矩阵）作为refine从而得到attention中的key。
• 3）bev的queries会在map embedding（bev grid通过embedding之后得到）下refine得到最后attention的queries。
• 4）使用CNN网络输出的多级特征图采用级联的方式refine bev特征，之后送入解码单元得到输出结果。

2.2 cross view attention

在3D情况下点空间点$x^{(W)}$和图像点$x^{(I)}$的映射关系为：
$$x^{(I)}\simeq K_k{R}_k(x^{(W)}-t_k)$$
也就是说上面的情况只是近似相等，应为不知道实际的深度值，所欲存在scale上的不确定性。而在这篇文章中并没有显式使用深度信息或者是隐式编码深度空间分布，而是将scale上的不确定性编码使用上述提到的camera-view embedding、map-view embedding和transformer网络进行学习和适应。而对于上述提到3D空间点$x^{(W)}$和图像点$x^{(I)}$的相似性关系使用的是余弦相似度：
$$si{m}_k(x^I,x^{(W)})=\frac{(R_k^{-1}{K}_k^{-1}{x}^{(I)})\cdot (x^W-t_k)}{||R_k^{-1}{K}_k^{-1}{x}^{(I)}||||x^W-t_k||}$$

camera-view embedding:
这里是在多视图特征维度结合各个视图的相机内外参数进行位置编码，也就是将特征图上的每个像素映射到3D空间其中去：
$$d_{k,i}=R_k^{-1}{K}_k^{-1}{x}_i^{(I)}$$
映射之后的3D点会经过线型网络进行编码得到camera-view embedding（${\delta }_{k,i}\in R^D$），参考下面代码：

# cross_view_transformer/model/encoder.py#L248
pixel_flat = rearrange(pixel, '... h w -> ... (h w)')                   # 1 1 3 (h w)
cam = I_inv @ pixel_flat                                                # b n 3 (h w)
cam = F.pad(cam, (0, 0, 0, 1, 0, 0, 0, 0), value=1)                     # b n 4 (h w)
d = E_inv @ cam                                                         # b n 4 (h w)
d_flat = rearrange(d, 'b n d (h w) -> (b n) d h w', h=h, w=w)           # (b n) 4 h w
d_embed = self.img_embed(d_flat)                                        # (b n) d h w

...

if self.feature_proj is not None:  # linear projection refine
    key_flat = img_embed + self.feature_proj(feature_flat)              # (b n) d h w
else:
    key_flat = img_embed                                                # (b n) d h w

更进一步该编码会减去相机位置编码${\tau }_k\in R^D$（其计算过程与上述camera-view embedding的计算过程类似），目的是为了估计道路上的每个单元的3D空间位置。则camera-view embedding的计算过程的不同对性能的影响见下表：

map-view embedding：
这部分是在bev grid embedding的基础上通过与相机位置编码${\tau }_k\in R^D$做差得到的（记为$c_j^n$），它与原本bev queries共同送入到transformer中完成attention，其实现可以参考：

# cross_view_transformer/model/encoder.py#L258
world = bev.grid[:2]                                                    # 2 H W
w_embed = self.bev_embed(world[None])                                   # 1 d H W
bev_embed = w_embed - c_embed                                           # (b n) d H W
bev_embed = bev_embed / (bev_embed.norm(dim=1, keepdim=True) + 1e-7)    # (b n) d H W
query_pos = rearrange(bev_embed, '(b n) ... -> b n ...', b=b, n=n)      # b n d H W

feature_flat = rearrange(feature, 'b n ... -> (b n) ...')               # (b n) d h w

...

# Expand + refine the BEV embedding
query = query_pos + x[:, None]                                          # b n d H W

cross-view attention：
将经过映射的多视图特征${\varphi }_{k,i}$（作为val）与上述得到的queries和key进行attention运算，对于文章说明其使用的是下面形式的余弦相似度：
$$sim({\delta }_{k,i},{\varphi }_{k,i},c_j^{(n)},{\tau }_{如何下载\; HuggingFace\; 模型“transformers.trainer.Trainer”？}$$

Transformers 和 PyTorch 的权重和偏差？

学习笔记Transformers库笔记

使用 Tensorflow 和 Transformers 标记数据帧

：Transformers 介绍

：Transformers 介绍