[Hot100]回文子串 与 最长回文子串

Posted 2022-06-29 王六六的IT日常

647. 回文子串
中等题
回文字符串 是正着读和倒过来读一样的字符串。
子字符串 是字符串中的由连续字符组成的一个序列。

①动态规划
状态：dp[i][j] 表示字符串s在[i,j]区间的子串是否是一个回文串。
状态转移方程：当 s[i] == s[j] && (j - i < 2 || dp[i + 1][j - 1]) 时，dp[i][j] = true，否则为dp[i][j] = false

状态转移方程的含义：

• 当只有一个字符时，比如 a 自然是一个回文串。
• 当有两个字符时，如果是相等的，比如 aa，也是一个回文串。
• 当有三个及以上字符时，比如 ababa 这个字符记作串 1，把两边的 a 去掉，也就是 bab 记作串 2，可以看出只要串2是一个回文串，那么左右各多了一个 a 的串 1 必定也是回文串。所以当 s[i]==s[j] 时，自然要看 dp[i+1][j-1] 是不是一个回文串。

class Solution 
    public int countSubstrings(String s) 
        //动态规划
        boolean[][] dp = new boolean[s.length()][s.length()];
        int res = 0;
        for(int i=s.length()-1;i>=0;i--)
            for(int j = i;j<s.length();j++)
                if(s.charAt(i) == s.charAt(j) && (j-i<=1 || dp[i+1][j-1]==true))
                    res++;
                    dp[i][j] = true;
                
            
        
        return res;
    

②中心扩展法
这是一个比较巧妙的方法，实质的思路和动态规划的思路类似。

比如对一个字符串 ababa，选择最中间的 a 作为中心点，往两边扩散，第一次扩散发现 left 指向的是 b，right 指向的也是 b，所以是回文串，继续扩散，同理 ababa 也是回文串。

这个是确定了一个中心点后的寻找的路径，然后我们只要寻找到所有的中心点，问题就解决了。

中心点一共有多少个呢？
看起来像是和字符串长度相等，但你会发现，如果是这样，上面的例子永远也搜不到 abab，想象一下单个字符的哪个中心点扩展可以得到这个子串？似乎不可能。所以中心点不能只有单个字符构成，还要包括两个字符，比如上面这个子串 abab，就可以有中心点 ba 扩展一次得到，分别是 len 个单字符和 len - 1 个双字符，所以最终的中心点有 (len + len -1) = 2 * len - 1 个。

如果上面看不太懂的话，还可以看看下面几个问题：

为什么有 2 * len - 1 个中心点？

• aba 有5个中心点，分别是 a、b、a、ab、ba
• abba 有7个中心点，分别是 a、b、b、a、ab、bb、ba
  什么是中心点？
  中心点即 left 指针和 right 指针初始化指向的地方，可能是一个也可能是两个
  为什么不可能是三个或者更多？
  因为 3 个可以由 1 个扩展一次得到，4 个可以由两个扩展一次得到

class Solution 
    public int countSubstrings(String s) 
        int n = s.length();
        int count = 0;
        //遍历每个位置
        for(int i=0;i<n;i++)
            //中心可能是1个字符 也可能是2个字符
            for(int j=0;j<=1;j++)
                int l = i;
                int r = i + j;
                while(l >= 0 && r < n && s.charAt(l) == s.charAt(r))
                    l--;
                    r++;
                    count++;
                
            
        
        return count;
    

5. 最长回文子串

中等题

①动态规划

我们用 P(i,j)表示字符串 s 的第 i 到 j 个字母组成的串（下文表示成 s[i:j]）是否为回文串：

这里的「其它情况」包含两种可能性：

s[i, j]本身不是一个回文串；
i > j，此时 s[i, j]、 本身不合法。

状态转移方程：
$$P(i,j)=P(i+1,j-1)且(S_i==S_j)$$

只有 s[i+1:j-1] 是回文串，并且 s 的第 i 和 j 个字母相同时，s[i:j] 才会是回文串。

• 对于长度为 1 的子串，它显然是个回文串；
• 对于长度为 2 的子串，只要它的两个字母相同，它就是一个回文串。

因此我们就可以写出动态规划的边界条件：

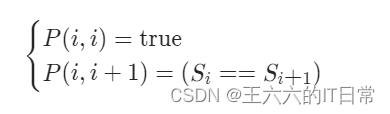
最终的答案即为所有 P(i,j)=true 中 j−i+1（即子串长度）的最大值。

注意：在状态转移方程中，我们是从长度较短的字符串向长度较长的字符串进行转移的，因此一定要注意动态规划的循环顺序。

public class Solution 

    public String longestPalindrome(String s) 
        int len = s.length();
        if (len < 2) 
            return s;
        

        int maxLen = 1;
        int begin = 0;
        // dp[i][j] 表示 s[i..j] 是否是回文串
        boolean[][] dp = new boolean[len][len];
        // 初始化：所有长度为 1 的子串都是回文串
        for (int i = 0; i < len; i++) 
            dp[i][i] = true;
        

        char[] charArray = s.toCharArray();
        // 递推开始
        // 先枚举子串长度
        for (int L = 2; L <= len; L++) 
            // 枚举左边界，左边界的上限设置可以宽松一些
            for (int i = 0; i < len; i++) 
                // 由 L 和 i 可以确定右边界，即 j - i + 1 = L 得
                int j = L + i - 1;
                // 如果右边界越界，就可以退出当前循环
                if (j >= len) 
                    break;
                

                if (charArray[i] != charArray[j]) 
                    dp[i][j] = false;
                 else 
                    if (j - i < 3) 
                        dp[i][j] = true;
                     else 
                        dp[i][j] = dp[i + 1][j - 1];
                    
                

                // 只要 dp[i][L] == true 成立，就表示子串 s[i..L] 是回文，此时记录回文长度和起始位置
                if (dp[i][j] && j - i + 1 > maxLen) 
                    maxLen = j - i + 1;
                    begin = i;
                
            
        
        return s.substring(begin, begin + maxLen);
    

②中心扩展法：

状态转移链：

$P(i,j)\leftarrow P(i+1,j-1)\leftarrow P(i+2,j-2)\leftarrow \cdots \leftarrow 某一边界情况$
所有的状态在转移的时候的可能性都是唯一的。也就是说，我们可以从每一种边界情况开始「扩展」，也可以得出所有的状态对应的答案。
边界情况即为子串长度为 1或 2 的情况。
本质：枚举所有的「回文中心」并尝试「扩展」，直到无法扩展为止，此时的回文串长度即为此「回文中心」下的最长回文串长度。我们对所有的长度求出最大值，即可得到最终的答案。

class Solution 
    public String longestPalindrome(String s) 
        if (s == null || s.length() < 1) 
            return "";
        
        int start = 0, end = 0;
        for (int i = 0; i < s.length(); i++) 
            int len1 = expandAroundCenter(s, i, i);
            int len2 = expandAroundCenter(s, i, i + 1);
            int len = Math.max(len1, len2);
            if (len > end - start) 
                start = i - (len - 1) / 2;
                end = i + len / 2;
            
        
        return s.substring(start, end + 1);
    

    public int expandAroundCenter(String s, int left, int right) 
        while (left >= 0 && right < s.length() && s.charAt(left) == s.charAt(right)) 
            --left;
            ++right;
        
        return right - left - 1;
    

参考：https://leetcode.cn/problems/longest-palindromic-substring/solution/zhong-xin-kuo-san-dong-tai-gui-hua-by-liweiwei1419/

public class Solution 

    public String longestPalindrome(String s) 
        int len = s.length();
        if(len < 2) return s;
        
        int maxLen = 0;
        // 数组第一位记录起始位置，第二位记录长度
        int[] res = new int[2];
        for (int i = 0; i < s.length() - 1; i++) 
            int[] odd = centerSpread(s, i, i);
            int[] even = centerSpread(s, i, i + 1);
            int[] max = odd[1] > even[1] ? odd : even;
            if (max[1] > maxLen) 
                res = max;
                maxLen = max[1];
            
        
        return s.substring(res[0], res[0] + res[1]);
    

    private int[] centerSpread(String s, int left, int right) 
        int len = s.length();
        while (left >= 0 && right < len) 
            if (s.charAt(left) == s.charAt(right)) 
                left--;
                right++;
             else 
                break;
            
        
        return new int[]left + 1, right - left - 1;
    

中心扩散的方法，其实做了很多重复计算。动态规划就是为了减少重复计算的问题。动态规划听起来很高大上。其实说白了就是空间换时间，将计算结果暂存起来，避免重复计算。
作用和工程中用 redis 做缓存有异曲同工之妙。