机器学习向量化计算 -- 机器学习路上必经路

Posted 2022-06-29 计算机魔术师

👋👋欢迎来到👋👋
🎩魔术之家！！🎩

该文章收录专栏
✨— 机器学习 —✨

专栏内容
✨— 【机器学习】浅谈正规方程法&梯度下降 —✨
✨— 【机器学习】梯度下降之数据标准化 —✨
✨— 【机器学习】logistic分类回归算法—✨
✨— 第十届“泰迪杯“感谢学习总结—✨

【机器学习】向量化计算 ---机器学习路上必经路

• 一、求解矩阵
• 二、例一
• 三、例二
• 四、写在最后

一、求解矩阵

在求解矩阵中，往往有很多很好的，经过高度优化的线性代数库，如octave，matlib，python numpy, c++,java.
我们使用这些线性代数库，可以短短几行实现 所要的效果。

阅读本文内容（需要一点点线性代数的知识）

二、例一

例如 求公式：

$h(x)={\sum }_{i=1}^n{\theta }_i\ast x_i$
我们可以通过循环每一个值来求 每一个$i$所对应的结果，但此时循环的时间复杂度为$O(n)$ ， 我们可以把 ${\theta }_i(i=1,2,3...n)$ 看为$n$维的列向量，$x_i$作为 $n$维的列向量，则原公式即为求两个向量的内积 ${\theta }^T\ast x_i$ 来求得方程，这样在numpy中仅仅需要一行代码。如下图（演示代码为octave(matlib开源版））

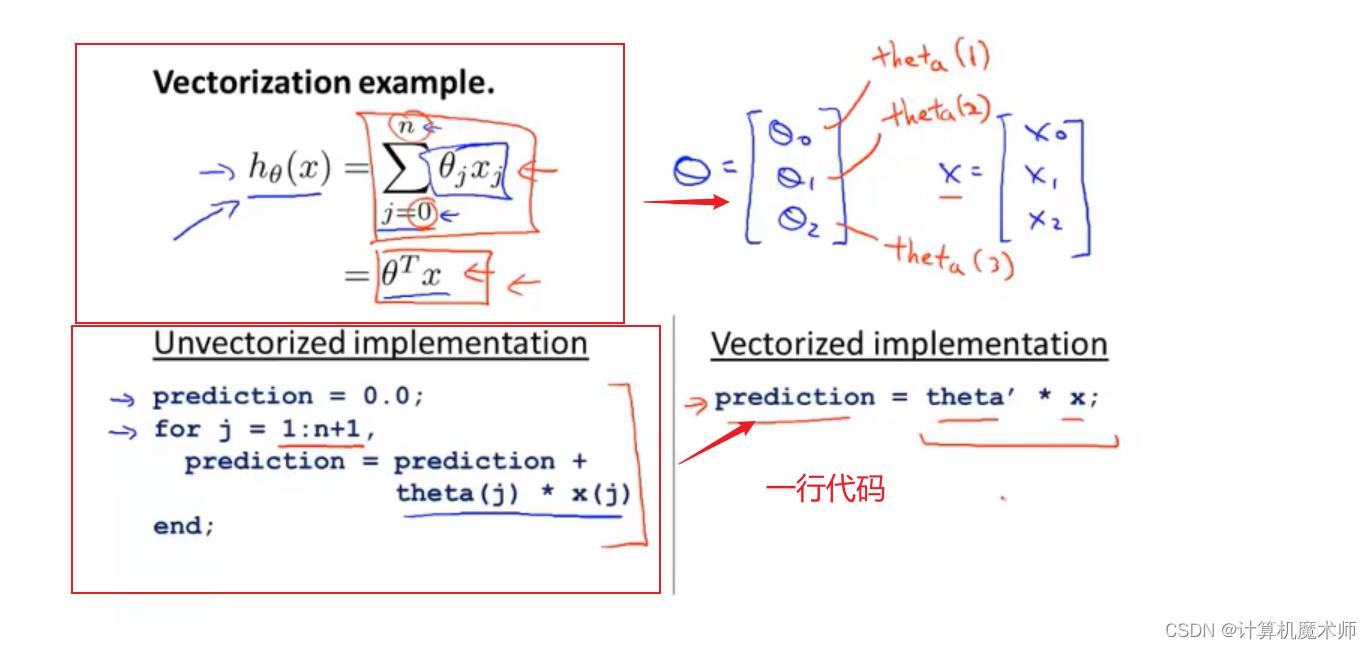
c++实现

三、例二

• 再看一个复杂一点的例子：

（对梯度下降还不了解建议先食用文章：机器学习】浅谈正规方程法&梯度下降）
在梯度下降(Gradient descent)同步更新参数${\theta }_i(i=1,2,3...m)中$

我们可以通过循环$i$得到每个参数更新，但我们是否能用例子一的方法 简化呢，

如图:

我们将所求式子变为 向量之间的运行，
$\theta =\theta -\alpha \ast \delta$
(其中：$\delta$ = ${\sum }_{x=1}^n\frac{（h_{\theta }(x)-y_i{）}^2}{n}\ast x_i$,$h_{\theta }(x)-y_i$ 是一个实数，$x_i$是特征维度的列向量)

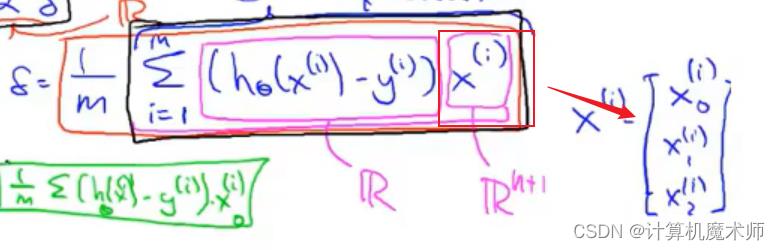
此时参数 ${\theta }_i$也能同步更新，符合要求

四、写在最后

在面对，数据为百万级别，千万级别，或者特征为百万级别，特征级别，向量化计算对提高运算效率非常高效，比for循环要好用得多，这在机器学习中是非常常见的，一定要掌握