总结用树形图和剪枝操作带你理解 完全背包问题中组合数和排列数问题

Posted 2022-06-24 Calculus2022

---

文章目录

• • @[TOC]
• 前言
• 一、完全背包中的排列数和组合数问题
• • 1.1 问题来源
  • 1.2 两个for循环先后顺序分析
  • • 1.2.1 先遍历背包后遍历物品得到排列数
    • 1.2.2 先遍历物品后遍历背包得到组合数
• 小结

---

前言

建议先看理清0-1背包问题和完全背包问题，再来看此博客，更加便于理解~~

一、完全背包中的排列数和组合数问题

1.1 问题来源

零钱兑换II

给定不同面额的硬币和一个总金额。写出函数来计算可以凑成总金额的硬币组合数。假设每一种面额的硬币有无限个。

首先明确：组合不强调元素之间的顺序，排列强调元素之间的顺序。

例如:
5 = 2 + 2 + 1
5 = 2 + 1 + 2
这是一种组合，都是 2 2 1。
如果问的是排列数，那么上面就是两种排列了。

如何实现统计的是组合数还是排列数呢？

• 关键在于内外两层遍历的顺序，即：本题中我们是外层for循环遍历物品（钱币），内层for遍历背包（金钱总额），还是外层for遍历背包（金钱总额），内层for循环遍历物品（钱币）。
• 对于完全背包问题的两个for循环的先后顺序都是可以的，这是因为因为纯完全背包求得是能否凑成总和，和凑成总和的元素有没有顺序没关系，即：有顺序也行，没有顺序也行。
• 本题是求凑出来的方案个数，且每个方案个数是为组合数，元素之间要求没有顺序，故要考虑两个for循环的顺序。

1.2 两个for循环先后顺序分析

对于coins = 1,2，5， amount = 5：

1.2.1 先遍历背包后遍历物品得到排列数

我们先来看 外层for遍历背包（金钱总额），内层for循环遍历物品（钱币）的情况。

for (int j = 0; j <= amount; j++)  // 遍历背包容量
    for (int i = 0; i < coins.length; i++)  // 遍历物品
        if (j - coins[i] >= 0) dp[j] += dp[j - coins[i]];
    

对于amount = 4 时 我们可以计算出 dp[4] = 5 即：
4 = 1 + 1 + 1 + 1
4 = 1 + 1 + 2
4 = 1 + 2 + 1
4 = 2 + 1 + 1
4 = 2 + 2
画成树形图 如下：可知此时我们得到的是排列数

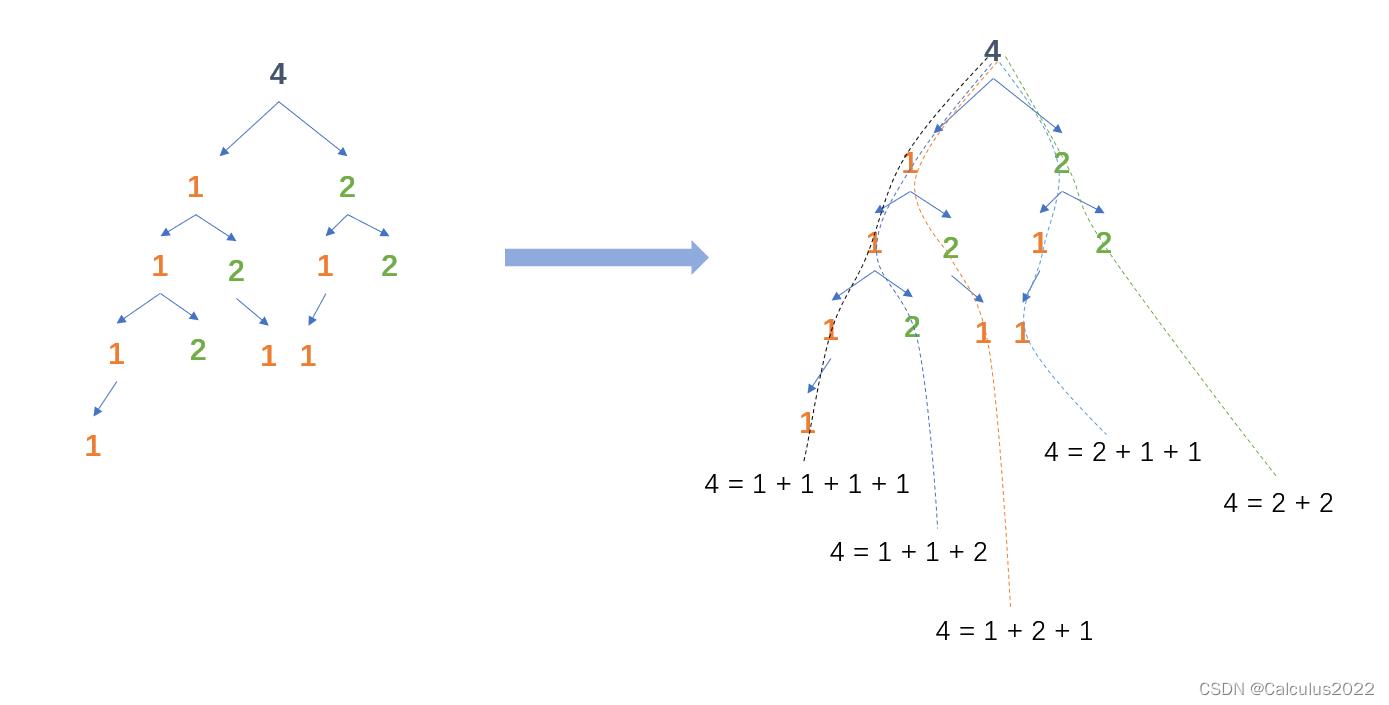
1.2.2 先遍历物品后遍历背包得到组合数

由上一节我们可知先遍历背包（金额总数）后遍历物品（物品）可得到排列数，那么如何得到组合数呢，观察上一小节中的树形图，我们进行剪枝：

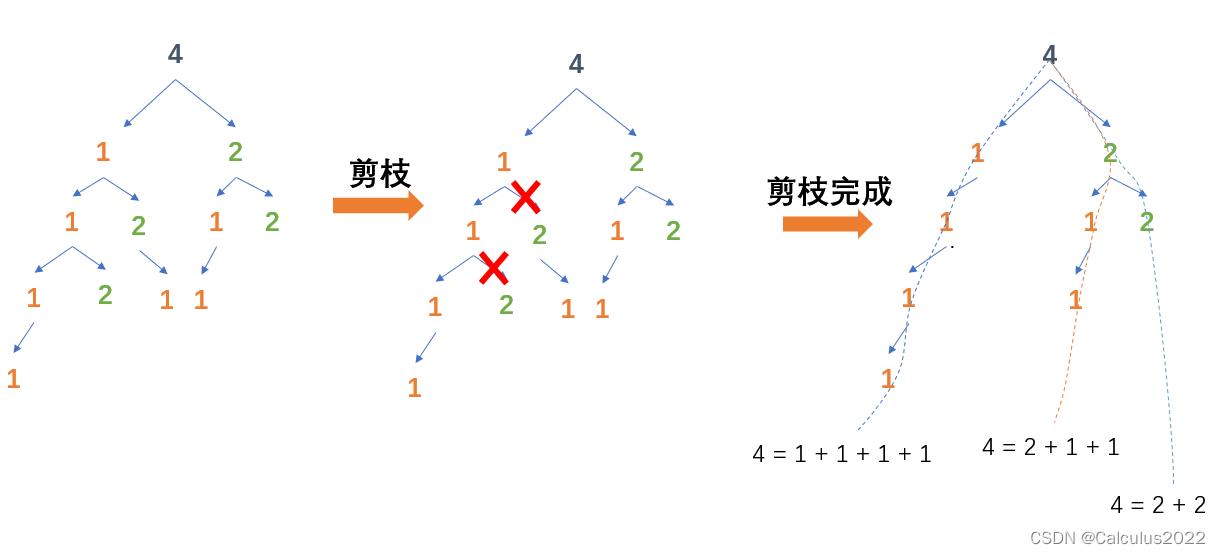
剪枝后我们得到
4 = 1 + 1 + 1 + 1
4 = 2 + 1 + 1
4 = 2 + 2
即剪去了
4= 4 = 1 + 1 + 2
4 = 1 + 2 + 1
此时得到组合数！！！

观察剪枝图片可知，此时等价于我们在计算硬币1如何组成4时，我们只考虑用硬币1；在计算硬币2如何组成4时，我们只考虑用硬币2和硬币1如何组成4。则即统计组合数的问题变成了：前 i个硬币凑齐金额 j 的方案数目。这就是先遍历物品（硬币）后遍历背包（金钱总额）！！！
实现代码为：

for (int i = 0; i < coins.length; i++)  // 遍历背包容量
    for (int j = 0; j <= amount; j++)  // 遍历物品
        if (j - coins[i] >= 0) dp[j] += dp[j - coins[i]];
    

小结

如果求组合数就是外层for循环遍历物品，内层for遍历背包。
如果求排列数就是外层for遍历背包，内层for循环遍历物品。
想要理解两种循环的区别，就从上面的树形图去理解~